
- •Параметрические уравнения прямой
- •2) Каноническое уравнение прямой на плоскости
- •3) Уравнение прямой, проходящей через две точки
- •29, 1. Общее уравнение плоскости
- •2. Другие формы записи уравнения плоскости
- •1) Уравнение плоскости, проходящей через точку параллельно двум неколлинеарным векторам
- •2) Уравнение плоскости, проходящей через три точки, не лежащие на одной прямой
- •2. Исследование
- •1. Уравнения прямой в пространстве
- •Каноническое уравнение эллипса (вывод)
- •Каноническое уравнение гиперболы в декартовой системе координат (вывод)
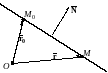
28,Получим общее уравнение прямой на плоскости, решив следующую задачу.
ЗАДАЧА
11.1. Записать уравнение прямой, проходящей
через точку
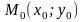 ,
перпендикулярно вектору
,
перпендикулярно вектору
 .
.
Пусть
точка
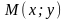 – произвольная точка прямой (такую
точку мы будем в дальнейшем называть
текущей точкой
прямой). Обозначим через
– произвольная точка прямой (такую
точку мы будем в дальнейшем называть
текущей точкой
прямой). Обозначим через
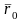 и
и
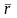 – радиус-векторы точек
– радиус-векторы точек
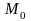 и
и
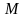 соответственно. Рассмотрим векторы
соответственно. Рассмотрим векторы

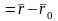 и
и
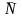 .
По условию задачи они перпендикулярны.
Следовательно,
.
По условию задачи они перпендикулярны.
Следовательно,
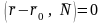 , (23)
, (23)
или, в координатной форме,
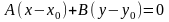 . (24)
. (24)
Уравнению (24) удовлетворяют координаты любой точки прямой и не удовлетворяют координаты других точек плоскости. Следовательно, это и есть искомое уравнение. Уравнения (23) и (24) называют уравнениями прямой, проходящей через точку перпендикулярно вектору (в векторной и координатной форме соответственно).
Раскроем скобки в уравнении (24) и приведем подобные слагаемые:
 .
.
Обозначим число
 через
через
 и получим общее
уравнение прямой на плоскости:
и получим общее
уравнение прямой на плоскости:
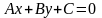 . (25)
. (25)
Таким
образом, прямая
в общем случае она задается уравнением
(25), где – числа.
Причем
– числа.
Причем
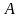 и
и
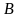 не обращаются в ноль одновременно, так
как с
геометрической точки зрения это
коэффициенты вектора, перпендикулярного
прямой.
не обращаются в ноль одновременно, так
как с
геометрической точки зрения это
коэффициенты вектора, перпендикулярного
прямой.
Вектор, перпендикулярный прямой, называют нормальнымвектором этой прямой.
Параметрические уравнения прямой
Получим параметрические уравнение прямой на плоскости, решив следующую задачу.
ЗАДАЧА
11.2. Записать уравнение прямой, проходящей
через точку
,
параллельно вектору
 .
.
Вектор, параллельный прямой, называют направляющим вектором этой прямой.
П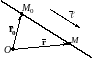 усть
точка
– текущая точка прямой. Обозначим через
и
– радиус-векторы точек
и
соответственно. Рассмотрим векторы
и
усть
точка
– текущая точка прямой. Обозначим через
и
– радиус-векторы точек
и
соответственно. Рассмотрим векторы
и
 .
По условию задачи они параллельны.
Следовательно, существует такое число
.
По условию задачи они параллельны.
Следовательно, существует такое число
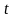 ,
что
,
что 
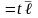 ,
,
⇒
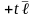 , (27)
, (27)
или, в координатной форме,
 (28)
(28)
Очевидно, что системе (28) будут удовлетворять координаты любой точки прямой при некотором значении ( называют параметром) и не будут удовлетворять координаты других точек плоскости.
Уравнение (27) и систему уравнений (28) называют параметрическимиуравнениями прямой (в векторной и координатной форме соответственно).
2) Каноническое уравнение прямой на плоскости
Если
в задаче 11.2 вектор
не параллелен ни одной из координатных
осей (т.е. если
 и
и
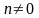 ),
то из уравнений системы (28) можно выразить
параметр
:
),
то из уравнений системы (28) можно выразить
параметр
:
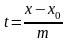 и
и
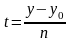 ,
,
и заменить систему (28) одним уравнением вида:

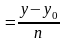 , (29)
, (29)
где
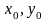 – координаты некоторой точки на прямой,
– координаты некоторой точки на прямой,
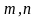 – координаты направляющего вектора
прямой.
– координаты направляющего вектора
прямой.
Уравнение (29) называют каноническим уравнением прямой на плоскости.
3) Уравнение прямой, проходящей через две точки
Это уравнение является частным случаем канонического уравнения прямой.
Д ействительно,
пусть прямая проходит через две точки
ействительно,
пусть прямая проходит через две точки
 и
и
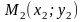 .
Тогда вектор
.
Тогда вектор

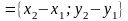 является ее направляющим вектором и
каноническое уравнение этой прямой
будет иметь вид
является ее направляющим вектором и
каноническое уравнение этой прямой
будет иметь вид
 . (30)
. (30)
Уравнение (30) называют уравнением прямой, проходящей через две точки и .
29, 1. Общее уравнение плоскости
Получим общее уравнение плоскости, решив следующую задачу.
ЗАДАЧА 12.1. Записать
уравнение плоскости, проходящей через
точку
 ,
перпендикулярно вектору
,
перпендикулярно вектору
 .
.
П усть
точка
усть
точка
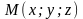 – текущая точка плоскости. Обозначим
через
и
–
радиус-векторы точек
и
соответственно. Рассмотрим векторы
и
.
По условию задачи они перпендикулярны.
Следовательно,
– текущая точка плоскости. Обозначим
через
и
–
радиус-векторы точек
и
соответственно. Рассмотрим векторы
и
.
По условию задачи они перпендикулярны.
Следовательно,
, (36)
или, в координатной форме,
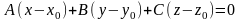 . (37)
. (37)
Уравнению (37) удовлетворяют координаты любой точки рассматриваемой плоскости и не удовлетворяют координаты других точек пространства. Следовательно, это и есть искомое уравнение. Уравнения (36) и (37) называют уравнениями плоскости, проходящей через точку перпендикулярно вектору (в векторной и координатной форме соответственно).
Раскроем скобки в уравнении (37) и приведем подобные слагаемые:
 .
.
Обозначим число
 через
через
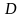 и получим общее уравнение плоскости:
и получим общее уравнение плоскости:
 (38)
(38)
Таким образом, плоскость
является поверхностью первого порядка.
В общем случае она задается уравнением
(38), где – числа. Причем
,
и
не
обращаются в ноль одновременно, так как
с геометрической точки зрения это
коэффициенты вектора, перпендикулярного
плоскости.
– числа. Причем
,
и
не
обращаются в ноль одновременно, так как
с геометрической точки зрения это
коэффициенты вектора, перпендикулярного
плоскости.
2. Другие формы записи уравнения плоскости
Рассмотрим в каком еще виде можно записать уравнение плоскости.
1) Уравнение плоскости, проходящей через точку параллельно двум неколлинеарным векторам
Решим следующую задачу.
З АДАЧА
12.2. Записать уравнение плоскости,
проходящей через точку
,
параллельно неколлинеарным векторам
АДАЧА
12.2. Записать уравнение плоскости,
проходящей через точку
,
параллельно неколлинеарным векторам
 и
и
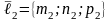 .
.
Пусть точка
– текущая точка плоскости. Обозначим
через
и
– радиус-векторы точек
и
соответственно. Рассмотрим векторы
,
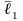 и
и
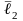 .
По условию задачи они компланарны.
Следовательно,
.
По условию задачи они компланарны.
Следовательно,
 , (40)
, (40)
или, в координатной форме,
 . (41)
. (41)
Уравнения (40) и (41) называют уравнениями плоскости, проходящей через точку параллельно двум неколлинеарным векторам (в векторной и координатной форме соответственно).
