4.4 Определение чисел зубьев в приводе

В группе передач соблюдается постоянство межосевого расстояния

(10)

где m – модуль;

Z_i – число зубьев соответствующего колеса или шестерни.

Следовательно, имея значения передаточных чисел, которые были посчитаны выше, можно выбрать из стандартного ряда сумм чисел оборотов [3]

Выбранные количества чисел зубьев будут приведены на кинематической схеме привода.

∑z		68	84	85
i	1,58	-	-	52:33
	1	34:34	42:42	-
	1,26	38:30	28:56	-
	0,79	30:38	17:67	-
	0,25	-	-	17:68

4.5 Разработка кинематической схемы привода

При разработке кинематической схемы привода необходимо учитывать компоновку станка, для которого он предназначается. У сверлильных станков коробка скоростей при небольшой высоте вертикально расположенных валов имеет значительные размеры в горизонтальном направлении.

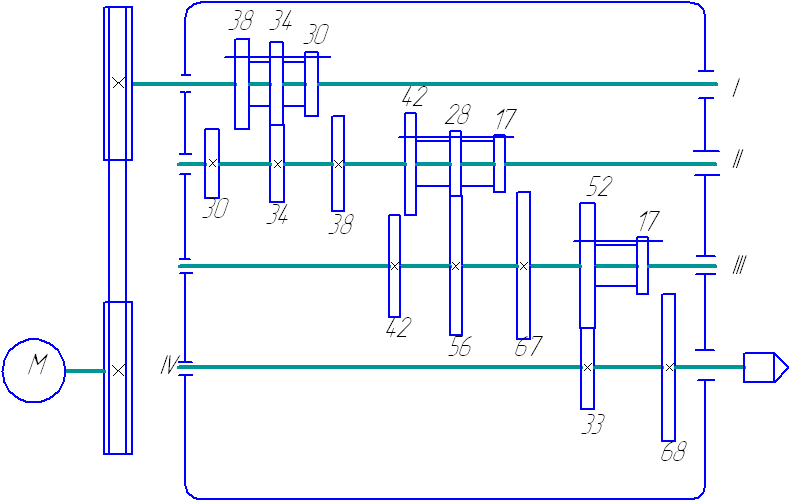
Рисунок 4 – Кинематическая схема привода главного движения с указанными числами зубьев соответствующих кинематических пар.

Также в схеме необходимо указать каким образом реализована передача крутящего момента с вала двигателя к приводу. В нашем случае момент передается клиноременной передачей. Ведущий шкив зафиксирован на валу с помощью шпонки и прижимного винта, ведомый расположен на первом валу привода.

5. Расчет зубчатых колёс.

Условия работы зубчатых передач даже в пределах одной кинематической группы значительно отличаются. Они существенно изменяются при включении тех или иных передач в другие кинематические группы.

Расчет зубчатых колес ведется на выносливость (усталость) поверхностных слоев по контактным напряжениям и на выносливость материала сердцевины зуба по напряжениям изгиба. Цепи главного привода передают полную мощность двигателя во всем диапазоне частот вращения шпинделя (или большей её части). Поэтому самым нагруженным является ведущее зубчатое колесо, так как усилия на его зубьях и число нагружений этих зубьев является наибольшими.

Номинальную нагрузку для универсальных станков среднего размера рекомендуется определить по верхней части диапазона частот вращения.

Расчет зубчатых колес может выполняться двояко: расчет модуля при выбранном материале и его термической обработке; либо при выбранных заранее геометрических размерах зубчатых колес, в форме расчета фактических величин, действующих контактных напряжений и напряжений изгиба с тем, чтобы по этим величинам назначать материал и термическую обработку для изготовления зубчатых колес.

Расчет в форме нахождения напряжений и назначения по ним материала зубчатого колеса и его термообработки, требует от разработчика конструкции определенного опыта и профессионального навыка при выборе модуля передачи, поэтому для курсового проекта за основную форму расчета как правило принимается расчет в форме определения модуля.

Согласно принятой нами кинематической схемы все зубчатые колеса в нашем приводе цилиндрические прямозубые.

Расчет цилиндрических прямозубых колес ведется:

- По напряжению изгиба по формуле, мм

, (11)

- По контактным напряжениям по формуле

, (12)

Где N – мощность, передаваемая рассчитываемой шестерней, определяется с учетом КПД передачи от двигателя до рассчитываемой шестерни, кВт;

n – расчетная частота вращения шестерни, об/мин, определяется по формуле

, (13)

где n_min и n_max – минимальная и максимальная частота вращения вала, на котором находится рассчитываемое зубчатое колесо;

z – число зубьев рассчитываемого зубчатого колеса;

i – передаточное отношение пары зубчатых колес, в которой работает рассчитываемое зубчатое колесо, понимаемое всегда, как отношение числа зубьев большего колеса к числу зубьев меньшего колеса. (всегда больше или равно еденице);

- отношение ширины зубчатого колеса (длины зуба) к модулю (обычно принимается равным (6-10));

y – коэффициент формы зуба (табл.1 [3]);

- допускаемое напряжение изгиба (табл.3 [3]);

- допускаемое напряжение (табл.3 [3]);

К_нер – коэффициент неравномерности распределения нагрузки по длине зуба в следствии деформации валов;

К_дин – коэффициент динамичности;

К – коэффициент долговечности.

Коэффициент долговечности при расчете на изгиб можно принять равным единице; при расчете по контактным напряжениям по формуле

, (14)

где К_N – коэффициент, характеризующий предполагаемое изменение мощности, передаваемой шестерней (табл.3 [3]).

К_n – коэффициент, характеризующий работу передачи на различных частотах вращения (табл.5 [3])

Т – расчетное время работы передачи, ч. для станков средних размеров принимается: для поочередно включенных передач (Х – число поочередно включаемых передач между смежными валами);

n_min – наименьшая частота вращения рассчитываемого зубчатого колеса в минуту;

N₀ – базовое число циклов нагружений для материала, рассчитываемого зубчатого колеса (табл.3).

Минимальное значение коэффициента долговечности К=1, предельно минимальное К=0,3. Если К получается больше единицы, его необходимо принять равным единице; если коэффициент долговечности получается меньше 0,3 его следует принять равным 0,3. Значения коэффициента К_N, характеризующего предполагаемое изменение мощности примем К_N=0,65(для универсальных станков).

Значение коэффициента К_n, характеризующего работу зубчатых колес на разных частотах вращения, примем К_n=1(работа на всем диапазоне частот вращения шпинделя с постоянной мощностью)

Величина коэффициента неравномерности К_нер зависит от условий монтажа зубчатых колес (в нашем случаи колеса расположены между опорами на валах нормальной жесткости К_нер=1).

Коэффициент К_дин учитывает дополнительные динамические нагрузки, возникающие из-за неточности изготовления зубчатых колес. Коэффициент динамичности К_дин определяется по формуле

, (15)

где b – ширина рассчитываемой шестерни (длина зуба), мм;

P – окружное усилие на зубе рассчитываемой шестерни;

, (16)

М – момент, передаваемый колесом, Н/м;

, (17)

где N₁ – мощность на валу на котором расположена рассчитываемое колесо,

U – динамическая нагрузка, приходящаяся на 1мм ширины шестерни (длина зуба), Н/мм, определяется по формуле

, (18)

где - окружная скорость на начальной шестерни, м/с;

А – межцентровое расстояние пары, мм;

- ошибка в шаге, мкм (табл.6 [3]);

i – передаточное отношение.

Поскольку для определения величины коэффициента динамичности К_дин необходимо знать размер рассчитываемой шестерни, т.е. величину её модуля, то весь расчет шестерни проведем в следующей последовательности (на примере расчета первого вала):

1. Сначала по формулам (11) и (12) находятся расчетные значения m, приняв К_дин=1.

;

;

2. По большему из полученных значений (m_изг и m_конт), путем округления его в большую сторону выбирается ближайшее нормализованное значение модуля. m_изг=2,033 примем ближайшее нормализованное (из первого ряда) m_изг=2.

3. В соответствии с выбранным значением m рассчитываем по формулам (15),(16) и (18) величину коэффициента динамичности К_дин.

Н;

Н/мм;

.

4. Полученное значение К_дин поставляем в ту из формул (11) или (12) по которой при первоначальном вычислении было получено большее значение модуля. Если при этом расчетная величина модуля, определенная с учетом К_дин, будет меньше или равно принятому значению нормализованного модуля, то, значит, принятый размер m достаточен, и расчет можно считать законченным. Если же она получается больше принятой нормализованной величины m, то надо увеличить принятую величину m до ближайшего большего значения по нормали, заново рассчитать величину К_дин и снова повторить расчет m по формулам (11) и (12).

мм < 3мм следовательно m=3 - достаточен.

Аналогично рассчитаем и для остальных валов.