1. Основы работы и расчета на устойчивость центрально сжатых стержней.

Исчерпание несушей способности длинных гибких стержней, работающих на осевое сжатие, происходит от потери устойчивости

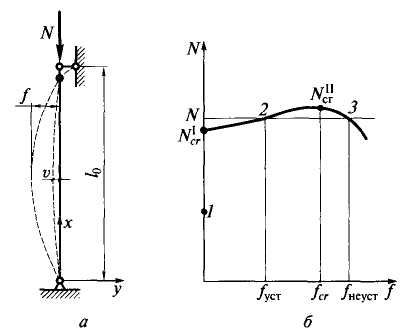
Работа центрально сжатого стержня:

а — расчетная схема; б — зависимость между нагрузкой и прогибом стержня

При фиксированномN = const, можно подсчитать приращение работ внешних dА_еи внутренних dАiсил.Если dAi>dAeто состояниеустойчивое, при dAi<dAe — неустойчивое, при dAi = dAe— критическим.

При изучении проблемы устойчивости стержней приращения работ на возможных перемещениях можно заменить приращениями соответствующих моментов dМеи dМiвследствие их прямой пропорциональной зависимости.При фиксированном N = const приращение момента внешних сил при возможном прогибе с амплитудой nравно dМе= Nn.Внутренних сил dМi = ρEI, где El — жесткость стержня; ρ = -у" — кривизна. Соответствующее критическое напряжение будет иметь вид:

Эта формула справедлива при напряжениях, не превышающих предел пропорциональностиs_cr<s_пц, при этом >√(Е/ _пц).Для мягких строительных сталей_пц = 20 кН/см2, следовательноl> 100. Для сталей повышенной прочности применимость формулы Эйлера ограничена значениемl>85. Следует заметить, что на практике гибкости центрально сжатых стержней (колонн, элементов ферм, рам и т.п.) в большинстве случаев составляют примерно половину указанных предельных.

2. Потеряют устойчивость в упругопластической стадии работы материала с касательным модулем деформации. Формула ф.С.Ясинского.

При lменьше предельных (Для мягких строительных сталей l> 100, для сталей повышенной прочности l>85) стержни теряют устойчивость в упругопластической стадии работы материала с касательным модулем деформации Е_t= ds/de< Е.

Н апряженно-деформированное

состояние центрально сжатого стержня: а — эпюра напряжений;

б— поперечное сечение стержня

Появляется дополнительный эксцентриситетапродольной силы. Приращение момента внешней силы dМ_е= N(n + а).Для внутренних сил d М_i определится суммой соответствующих интегралов по площадям А₁и А₂ разделенным нейтральной осью 2—2.

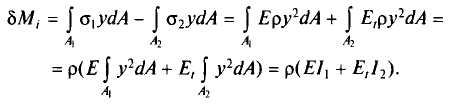
Тогда dМ_I= ρTJ, гдеТпредставляет собой приведенный модуль деформации, определяемый из равенства TJ=EJ₁+E _T J₂. Откуда

Введение понятия приведенного модуляТэквивалентно замене стержня из разнородного материала (участок А₁подчиняется упругому закону, участок А₂— пластическому) стержнем из однородного материала с уменьшенным модулем упругости.

Продолжая цепочку выкладок, напишем:

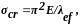
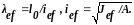
До сих пор рассматривался идеально прямой стержень с нагрузкой, приложенной строго по оси. В реальных конструкциях таких условий практически не существует. Ось стержня всегда имеет некоторые искривления, конструктивное оформление концов сжатых стержней не может обеспечить идеальную центровку сжимающей силы, что приводит к заметному снижению критических напряжений. Учет влияния указанных факторов осуществляется введением в расчет некоторого эквивалентного эксцентриситета сжимающей силы e_ef. Этот эксцентриситет зависит от многих случайных факторов: технологии изготовления, транспортировки, монтажа, конструктивного решения стержня и его узлов и т.д.

Статистические исследования эксцентриситетов показывают их зависимость от гибкости стержня — они возрастают с ростом гибкости. Поэтому в практических расчетах используют критическое напряжение, вычисленное с учетом случайных эксцентриситетов _cr,е.

З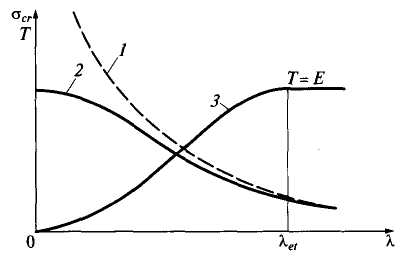 ависимость критических напряжений и приведенного модуля деформаций от гибкости стержня:

1 — кривая Эйлера; 2 — кривая критических напряжений для сталей типа СтЗ; 3 — график модуляТ