3.Метод Адама решения задачи Коши(общая схема метода, явные неявные методы, явный метод 3-го порядка, неявный метод 3-го порядка)

Многошаговые методы решения задач Коши для ОДУ

Методы решения ОДУ бывают одношаговые и многошаговые. К одношаговым относятся: метод Эйлера, метод Рунге – Кутты и др., а к многошаговым: линейные многошаговые разностные методы, в том числе методы Адамса-Башфорта и методы Адамса-Мултона.

В многошаговых методах повышение точность вычисления происходит за счет использования информации о поведении решения на предыдущих шагах.

Общая схема построения m-шаговых разностных методов, используемых для приближенного решения задачи Коши [4]

(1)

выглядит следующим образом

(2)

где - числовые коэффициенты, не зависящие от n, причем .Уравнение (2) следует рассматривать как рекуррентное соотношение, выражающее новое значение через найденные ранее значения .

Наиболее простые и наиболее часто встречающиеся вычислительные правила для многошаговых методов имеют вид:

(3)

Среди правил (5) особенно широко известны явные (экстраполяционные) при и неявные (интерполяционные) при методы Адамса.

 

3.1 Явные многошаговые методы Адамса-Башфорта

Все m –шаговые методы Адамса, полученные из формулы (3), положив в ней получили название явные методы Адамса-Башфорта или э кстраполяционные методы Адамса

(4)

Определить коэффициенты формулы (4) можно следующим образом. Пусть известно приближенное решение в m узлах сетки . Следовательно, в этих точках отрезка известно и значение правой части дифференциального уравнения (1) при i=n-m+1, ...,n-1,n, причем будет уже функцией только одной переменной . Заменим в (6) функцию интерполяционным многочленом , например, многочленом Ньютона и вычислим значение , проинтегрировав (1) на отрезке . Находим

(5)

Проводя интегрирование, получим разностную схему для решения дифференциального уравнения. Порядок схемы определяется величиной остаточного члена интерполяционного полинома. По существу, интерполяционный многочлен в формуле (5) используется вне области, т.е. в данном случае это экстраполяционный многочлен. Поэтому полученный таким образом метод часто называют экстраполяционным методом Адамса - Башфорта. Получим формулы Адамса - Башфорта для различного числа точек m. Зададим таблицу , заданных значений приближенного решения, по которым можно вычислить значения и составить таблицу .

Рассмотрим случай при m =2. В этом случае соответствующий многочлен Ньютона будет иметь вид:

Н1(t)=Fn+(t-tn)F(tn,tn-1)=Fn+(t-tn)(Fn-Fn-1)/h.

Подставив его в формулу (7) мы получим:

А после интегрирования формула для вычисления приближенного решения будет иметь вид:

 

3. 2 Неявные многошаговые методы Адамса-Мултона

Неявные m-шаговые методы Адамса определяются формулой (6) при . Их также называют интерполяционные методы Адамса-Мултона.

(6)

Построение интерполяционных m- шаговых методов Адамса-Мултона может быть осуществлено совершенно аналогично случаю экстраполяционных формул. Для этого следует использовать интеграл (5) , в котором интерполяционный многочлен построен по следующим узлам интерполяции .

Приведем интерполяционные формулы Адамса различных порядков точности:

двухшаговый неявный разностный метод Адамса- Мултона

(7)

трехшаговый неявный разностный метод Адамса – Мултона

(8)

Определение порядка аппроксимации неявных методов Адамса-Мултона выполняется аналогично определению невязки методов Адамса-Башфорта

Погрешность аппроксимации трех шагового метода Адамса – Мултона равна

Заметим, что во всех приведенных выше интерполяционных формулах Адамса значение неизвестно, так как само пока является неизвестным. Следовательно, интерполяционные методы Адамса определяют только неявно. Так, например, интерполяционная формула второго порядка точности

(9)

действительно является уравнением относительно неизвестного значения . Поэтому интерполяционный метод Адамса называют неявным.

На практике обычно не решают уравнение (9), а используют совместно явную и неявную формулы (метод Адамса-Бошфорта-Мултона), что приводит к методу прогноза и коррекции. Одним из широко используемых методов прогноза и коррекции является объединение методов Адамса четвертого порядка точности

(10)

При такой последовательности вычислений этот метод является явным

4.Моделирование случайных величин(равномерной, нормальной, с произвольным законом распределения)

Часто на практике встречаются системы случайных величин, то есть такие две (и более) различные случайные величины X, Y (и другие), которые зависят друг от друга. Например, если произошло событие X и приняло какое-то случайное значение, то событие Y происходит хотя и случайно, но с учетом того, что X уже приняло какое-то значение.

Например, если в качестве X выпало большое число, то Y должно выпасть тоже достаточно большое число (если корреляция положительна). Весьма вероятно, что если человек имеет большой вес, то он, скорее всего, будет и большого роста. Хотя это НЕ ОБЯЗАТЕЛЬНО, это НЕ ЗАКОНОМЕРНОСТЬ, а корреляция случайных величин. Так как бывают, хотя и редко, люди с большим весом, но небольшого роста или с маленьким весом и высокие. И все таки основная масса тучных людей — высоки, а низких людей — имеют малый вес.

По определению, если случайные величины независимы, то f(x) = f(x₁) · f(x₂) · … · f(x_n).

xi — случайная независимая величина; f(xi) — плотность вероятности выпадения случайной независимой величины xi; f(x) — плотность вероятности выпадения вектора x случайных независимых величин x1, x2, …, xn.

Если случайные величины зависимы, то f(x) = f(x₁) · f(x₂ | x₁) · f(x₃ | x₂, x₁) · … · f(x_n | x_n – 1, x_n – 2, …, x₂, x₁).

xj | xj – 1, …, x1 — случайные зависимые величины: выпадение xj при условии, что выпали xj – 1, …, x1; f(xj | xj – 1, …, x1) — плотность условной вероятности появления xj, если выпали xj – 1, …, x1; f(x) — вероятность выпадения вектора x случайных зависимых величин.

Моделирование нормально распределенных случайных величин

Нормальный закон распределения встречается в природе весьма часто, поэтому для него разработаны отдельные эффективные методы моделирования. Формула распределения вероятности значений случайной величины x по нормальному закону имеет вид:

Как видно, нормальное распределение имеет два параметра: математическое ожидание m_x и среднеквадратичное отклонение σ_x величины x от этого математического ожидания.

x — случайная величина; y(x) — вероятность принятия случайной величиной значения x; mx — математическое ожидание; σx — среднее квадратичное отклонение.

Нормализованным нормальным распределением называется такое нормальное распределение, у которого m_x = 0 и σ_x = 1. Из нормализованного распределения можно получить любое другое нормальное распределение с заданными m_x и σ_x по формуле: z = m_x + x · σ_x.

Рассматривая последнюю формулу, вспомните формулы компьютерной графики: операция масштабирования выражается в математической модели через умножение (это соответствует изменению разброса величины, растягиванию геометрического образа), операция смещения выражается через сложение (это соответствует изменению значения наиболее вероятной величины, смещению геометрического образа).

Функция нормального распределения имеет вид колокола. На рис. 25.1 показано нормализованное нормальное распределение.

Рис. 25.1. Графический вид нормального закона распределения случайной величины х с параметрами mx = 0 и σx = 1 (распределение нормализовано)

График на рис. 25.1 показывает, что в области –σ < x < σ на графике сосредоточено 68% площади распределения, в области –2σ < x < 2σ на графике сосредоточено 95.4% площади распределения, в области –3σ < x < 3σ на графике сосредоточено 99.7% площади распределения («правило трех сигм»). Вспомните, пожалуйста, рис. 2.7 из лекции 02.

Пример. По нормальному распределению распределен рост людей, находящихся одновременно в большой аудитории. А именно: достаточно мало людей очень большого роста, и столь же мала вероятность встретить людей очень малого роста. В основном, легче встретить людей среднего роста — и вероятность этого велика.

Например, средний рост людей составляет, в основном, 170 см, то есть m_x = 170. Известно также, что σ_x = 20. На рис. 25.1 показано, что доля людей с ростом от 150 до 190 (170 – 20 < 170 < 170 + 20) составляет в обществе 68%. Доля людей от 130 см до 210 см (170 – 2 · 20 < 170 < 170 + 2 · 20) составляет в обществе 95.4%. Доля людей от 110 см до 230 (170 – 3 · 20 < 170 < 170 + 3 · 20) составляет в обществе 99.7%. Например, вероятность того, что человек окажется ростом меньше 110 см или больше 230 см составляет всего 3 человека на 1000.

5. Проверка гипотезы о заданном законе распределения Критерий Пирсона.

Критерий Пирсона, или критерий χ² (Хи-квадрат) — наиболее часто употребляемый критерий для проверки гипотезы о законе распределения. Во многих практических задачах точный закон распределения неизвестен, то есть является гипотезой, которая требует статистической проверки.

Обозначим через X исследуемую случайную величину. Пусть требуется проверить гипотезу о том, что эта случайная величина подчиняется закону распределения . Для проверки гипотезы произведём выборку, состоящую из n независимых наблюдений над случайной величиной X. По выборке можно построить эмпирическое распределение исследуемой случайной величины. Сравнение эмпирического распределения и теоретического (или, точнее было бы сказать, гипотетического — то есть соответствующего гипотезе ) распределения производится с помощью специального правила — критерия согласия. Одним из таких критериев и является критерий Пирсона.

Для проверки критерия вводится статистика:

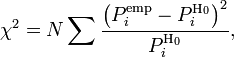
где  — предполагаемая вероятность попадания в -й интервал,  — соответствующее эмпирическое значение,  — число элементов выборки из -го интервала,  — полный объём выборки. Также используется расчет критерия по частоте, тогда:

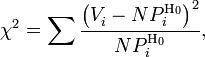
где  — частота попадания значений в интервал. Эта величина, в свою очередь, является случайной (в силу случайности ) и должна подчиняться распределению .

Правило. Если полученная статистика превосходит квантиль закона распределения заданного уровня значимости с или с степенями свободы, где — число наблюдений или число интервалов (для случая интервального вариационного ряда), а — число оцениваемых параметров закона распределения, то гипотеза отвергается. В противном случае гипотеза принимается на заданном уровне значимости .

6. Точные методы решения систем линейных уравнений (метод Гаусса, LU-разложения).

Метод Гаусса

Метод Гаусса является прямым методом. Запишем систему линейных уравнений в виде:

.................................................................                                          (4.1а)

Пусть  Выполнения этого условия всегда можно добиться перенумерацией компонент вектора x, либо перестановками уравнений. Тогда запишем первое из уравнений (4.1а) в виде

                                             (4.2)

Вычтем это уравнение, умноженное на соответствующий коэффициент  из i-го уравнения системы (4.1а), где i > 1. Тогда эти уравнения преобразуются к виду

.................................................................                                            (4.3)

Первая компонента вектора x не входит в подсистему (4.3). Выполним с (4.3) те же операции, что и ранее с системой уравнений (4.1а). В результате получим новую подсистему уравнений, в которую уже не будут входить  и  Она дополняется уравнением (4.2) и первым уравнением системы (4.3), не содержащим  Уже после m – 3 подобных циклов мы получаем подсистему из одного уравнения с одним неизвестным. При этом матрица системы будет иметь треугольный вид. Совокупность операций по приведению системы уравнений к такому виду называется прямым ходом метода Гаусса. Решение системы с треугольной матрицей не вызывает затруднений. Совокупность операций по нахождению решения системы с треугольной матрицей называется обратным ходом метода Гаусса.

Общее число арифметических операций при решении системы (4.1а) методом Гаусса составляет

В приложениях матрица A часто имеет трехдиагональный вид, т. е. ненулевые элементы матрицы располагаются на главной диагонали и двух близлежащих к ней. Применение метода Гаусса к такой системе уравнений называется методом прогонки.

Метод Гаусса может оказаться неустойчивым по отношению к росту вычислительной погрешности.

Теорема 1. Для устойчивости метода Гаусса достаточно диагонального преобладания, т. е. выполнения неравенств

d > 0, i = 1, 2, …, m.

Вычислительную погрешность метода Гаусса можно уменьшить, если применить модификацию метода, называемую методом Гаусса с выделением главного элемента. Суть этой модификации заключается в следующем. Нумерация компонент вектора x и уравнений выбирается так, чтобы  являлся максимальным по модулю элементом матрицы A. Затем, после исключения  перенумерацией строк и столбцов добиваются того, чтобы  в (4.3) являлся максимальным по модулю элементом матрицы системы (4.3). Подобная процедура продолжается и далее.

При расчете на реальной ЭВМ с заданным числом разрядов, наряду с влиянием неточного задания входных данных на каждой арифметической операции, вносятся ошибки округления. Влияние последних на результат зависит не только от разрядности машины, но и от числа обусловленности матрицы системы, а также от выбранного алгоритма. Существуют алгоритмы, учитывающие влияние ошибок округления и позволяющие получить результат с гарантированной точностью, если система не обусловлена настолько плохо, что при расчете с заданной разрядностью эта точность не может быть гарантирована.

LU-разложение

LU-разложение — представление матрицы в виде произведения двух матриц, , где  — нижняя треугольная матрица, а  — верхняя треугольная матрица. LU-разложение еще называют LU-факторизацией.

LU-разложение используется для решения систем линейных уравнений, обращения матриц и вычисления определителя.

Этот метод является одной из разновидностей метода Гаусса.

Решение систем линейных уравнений

LU-разложение может быть использовано для решения системы линейных уравнений

где — матрица коэффициентов системы, — вектор неизвестных величин системы, — вектор правых частей системы.

Если известно LU-разложение матрицы , , исходная система может быть записана как

Эта система может быть решена в два шага. На первом шаге решается система

Поскольку — нижняя треугольная матрица, эта система решается непосредственно прямой подстановкой.

На втором шаге решается система

Поскольку — верхняя треугольная матрица, эта система решается непосредственно обратной подстановкой.

Обращение матриц

Обращение матрицы эквивалентно решению линейной системы

,

где — неизвестная матрица, — единичная матрица. Решение этой системы является обратной матрицей .

Систему можно решить описанным выше методом LU-разложения.

Вычисление определителя матрицы

Имея LU-разложение матрицы ,

,

можно непосредственно вычислить её определитель,

,

где — размер матрицы , и — диагональные элементы матриц и .

Вывод формулы

В силу назначения LU-разложения нас будет интересовать только случай, когда матрица A невырождена.

Поскольку и в первой строке матрицы L, и в первом столбце матрицы U, все элементы, кроме, возможно, первого, равны нулю, имеем

Если , то или . В первом случае целиком состоит из нулей первая строка матрицы L, во втором — первый столбец матрицы U. Следовательно, L или U вырождена, а значит, вырождена A, что противоречит предположению. Таким образом, если , то невырожденная матрица A не имеет LU-разложения.

Пусть , тогда и . Поскольку L и U определены с точностью до умножения U на константу и деления L на ту же константу, мы можем потребовать, чтобы . При этом .

Разделим матрицу A на клетки:

,

где имеют размерность соответственно (N-1)×1, 1×(N-1), (N-1)×(N-1). Аналогично разделим на клетки матрицы L и U:

Уравнение

принимает вид

Решая систему уравнений относительно , получаем:

Окончательно имеем:

Итак, мы свели LU-разложение матрицы N×N к LU-разложению матрицы (N-1)×(N-1).

Выражение называется дополнением Шура элемента в матрице A.

Заметим, что  — не скаляр, а матрица (N-1)×(N-1).

Алгоритм

Один из алгоритмов для вычисления LU-разложения приведён ниже.

Будем использовать следующие обозначения для элементов матриц , , ; причём диагональные элементы матрицы : , . Тогда, если известно LU-разложение матрицы, её определитель можно вычислить по формуле = произведению элементов на диагонали матрицы U.

Найти матрицы и можно следующим образом (выполнять шаги следует строго по порядку, так как следующие элементы находятся с использованием предыдущих):

1. 

2. 

Для

1. 

2. 

В итоге мы получим матрицы — и . В программной реализации данного метода (компактная схема Гаусса) для представления матриц и можно обойтись всего одним массивом, в котором совмещаются матрицы и . Например, так (для матрицы размером ):

7.Симметричные матрицы, разложения Холецкого (применения к решению систем линейных уравнений)

Разложение Холецкого

Разложе́ние Холе́цкого — представление симметричной положительно-определённой матрицы в виде , где — нижняя треугольная матрица со строго положительными элементами на диагонали. Иногда разложение записывается в эквивалентной форме: , где — верхняя треугольная матрица. Разложение Холецкого всегда существует и единственно для любой симметричной положительно-определённой матрицы.

Существует также обобщение этого разложения на случай комплекснозначных матриц. Если — положительно-определённая эрмитова матрица, то существует разложение , где — нижняя треугольная матрица с положительными действительными элементами на диагонали, а — эрмитово-сопряжённая к ней матрица.

Разложение названо в честь французского математика Андре-Луи Холецкого (1875-1918).

Алгоритм

Элементы матрицы можно вычислить, начиная с верхнего левого угла матрицы, по формулам:

, если .

Выражение под корнем всегда положительно, если — действительная положительно-определённая матрица.

Вычисление происходит сверху вниз, слева направо,т.е. сперва , а затем .

Для комплекснозначных эрмитовых матриц используются формулы:

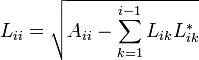
, если .

Приложения

Это разложение может применяться для решения системы линейных уравнений , если матрица симметрична и положительно-определена. Такие матрицы часто возникают, например, при использовании метода наименьших квадратов и численном решении дифференциальных уравнений.

Выполнив разложение , решение получается последовательным решением двух треугольных систем уравнений: и . Такой способ решения иногда называется методом квадратных корней.^[1] По сравнению с более общими методами, такими как метод Гаусса или LU-разложение, он устойчивее численно и требует примерно вдвое меньше арифметических операций. ^[2]

Разложение Холецкого также применяется в методах Монте-Карло для генерации коррелированных случайных величин. Пусть  — вектор из независимых стандартных нормальных случайных величин, а  — желаемая ковариационная матрица. Тогда вектор будет иметь многомерное нормальное распределение с нулевым математическим ожиданием и ковариационной матрицей . ^[3]

8.Обусловленность сиситем линейных уравнений. Число обусловленности матрицы.

Обусловленность систем линейных уравнений

Две на первый взгляд похожие системы линейных уравнений могут обладать различной чувствительностью к погрешностям задания входных данных. Это свойство связано с понятием обусловленности системы уравнений.

Числом обусловленности линейного оператора A, действующего в нормированном пространстве  а также числом обусловленности системы линейных уравнений Ax = f назовем величину

Таким образом, появляется связь числа обусловленности с выбором нормы.

Предположим, что матрица и правая часть системы заданы неточно. При этом погрешность матрицы составляет A, а правой части — f. Можно показать, что для погрешности x имеет место следующая оценка ( ):

В частности, если A = 0, то

При этом решение уравнения Ax = f не при всех f одинаково чувствительно к возмущению f правой части.

Свойства числа обусловленности линейного оператора:

1. 

причем максимум и минимум берутся для всех таких x, что  Как следствие,

2. 

3 

где  и  — соответственно минимальное и максимальное по модулю собственные значения матрицы A. Равенство достигается для самосопряженных матриц в случае использования евклидовой нормы в пространстве

4. 

Матрицы с большим числом обусловленности (ориентировочно ) называются плохо обусловленными матрицами. При численном решении систем с плохо обусловленными матрицами возможно сильное накопление погрешностей, что следует из оценки для погрешности x. Исследуем вопрос о погрешности решения, вызванной ошибками округления в ЭВМ при вычислении правой части. Пусть t — двоичная разрядность чисел в ЭВМ. Каждая компонента  вектора правой части округляется с относительной погрешностью  Следовательно,

Таким образом, погрешность решения, вызванная погрешностями округления, может быть недопустимо большой в случае плохо обусловленных систем.

Число обусловленности

В численных методах, число обусловленности характеризует точность решения задачи и является мерой аменабельности этого решения в численном представлении, то есть насколько задача хорошо или плохо обусловлена.

Число обусловленности для оператора

Пусть задан ограниченный обратимый линейный оператор . Числом обусловленности (другое обозначение — ) оператора называется число

Если оператор не ограничен, то числом обусловленности оператора обычно считают

С числом обусловленности связано множество утверждений и оценок теории вычислительной математики.

Рассмотрим линейное уравнение

,

где  — линейный оператор,  — вектор,  — искомый вектор (переменная уравнения). Допустим, уравнение решается с погрешностью на входных данных. Тогда число обусловленности характеризует, насколько велика будет погрешность решения.

Если число обусловленности оператора мало́, то оператор называется хорошо обусловленным. Если же число обусловленности велико, то оператор называется плохо обусловленным. Таким образом, чем меньше , тем «лучше», то есть тем меньше погрешности решения будут относительно погрешностей в условии. Учитывая, что , то наилучшим числом обусловленности является 1.

Некоторые теоремы, связанные с числом обусловленности

Оценка относительной погрешности при замене уравнения близким

Рассмотрим два линейных уравнения:

 — «основное» уравнение

 — «близкое» к нему.

Пусть  — линейный ограниченный обратимый оператор, действующий из полного пространства . Пусть операторы также ограничены, и .

Пусть  — решение уравнения (1),  — решение уравнения (2).

Тогда   

9.Итерационные методы решения систем линейных уравнений, одношаговые стационарные методы ( Якоби, Зейделя, простой итерации)

Рассматривается система Ax = b.  Для применения итерационных методов система должна быть приведена к эквивалентному виду x=Bx+d. Затем выбирается начальное приближение к решению системы уравнений   и находится последовательность приближений к корню. Длясходимости итерационного процесса достаточно, чтобы было выполнено условие  . Критерий окончания итераций зависит от применяемого итерационного метода.

 

Метод Якоби.

Самый простой способ приведения системы к виду удобному для итерации состоит в следующем: из первого уравнения системы выразим неизвестное  x₁, из второго уравнения системы выразим  x₂, и т. д. В результате получим систему уравнений с матрицей B, в которой на главной диагонали стоят нулевые элементы, а остальные элементы вычисляются по формулам:

  ,    i, j = 1, 2, ... n.

Компоненты вектора d вычисляются по формулам:

  ,   i = 1, 2, ... n.

Расчетная формула метода простой итерации имеет вид

,

или в покоординатной форме записи выглядит так:

,  i = 1, 2, ... m.

Критерий окончания итераций в методе Якоби имеет вид:

 ,   где    .

Если   , то можно применять более простой критерий

 окончания итераций

ПРИМЕР 1. Решение системы линейных уравнений методом Якоби.

Метод Зейделя.

Метод можно рассматривать как модификацию метода Якоби. Основная идея состоит в том, что при вычислении очередного (n+1)-го приближения к неизвестному  x_i при i >1 используют уже найденные (n+1)-е приближения к неизвестным  x₁, x₂, ..., x_{i - 1}, а не n-ое приближение, как в методе Якоби. Расчетная формула метода в покоординатной форме записи выглядит так:

,

 i = 1, 2, ... m.. Условия сходимости и критерий окончания итераций можно взять такими же как в методе Якоби.

ПРИМЕР 2. Решение систем линейных уравнений методом Зейделя.

 

Пусть матрица системы уравнений A - симметричная и положительно определенная. Тогда при любом выборе начального приближения метод Зейделя сходится. Дополнительных условий на малость нормы некоторой матрицы здесь не накладывается.

Метод простой итерации.

Если A - симметричная и положительно определенная матрица, то систему уравнений часто приводят к эквивалентному виду:

x = x -  (Ax - b),    - итерационный параметр.

Расчетная формула метода простой итерации в этом случае имеет вид:

x ⁽ⁿ⁺¹⁾ = x ⁿ -   (Ax ⁿ - b).

Здесь B = E -   A  и параметр    > 0 выбирают так, чтобы по возможности сделать минимальной величину   .

Пусть   и   - минимальное и максимальное собственные значения матрицы A. Оптимальным является выбор параметра   . В этом случае   принимает минимальное значение равное  .

10.Общая постановка задачи регрессии. Матрица плана, информационная матрица, определение коэффициентов регрессии.

Линия регрессии

•  Вычисляемая с помощью метода наименьших квадратов прямая линия называется линией регрессии . Она характеризуется тем, что сумма квадратов расстояний от точек на диаграмме до этой линии минимальна (по сравнению со всеми возможными линиями).

•  Линия регрессии дает наилучшее приближенное описание линейной зависимости между двумя переменными.

Уравнение парной линейной регрессии

•  Как известно, прямая линия описывается уравнением вида:

Y = kX + b

где Y – результирующий признак, X – факторный признак, k и b – числовые параметры уравнения.

•  Коэффициент k в уравнении регрессии называется коэффициентом регрессии .

Смысл коэффициента регрессии

•  В общем случае коэффициент регрессии k показывает, как в среднем изменится результативный признак ( Y ), если факторный признак ( X ) увеличится на единицу .

Пример уравнения регрессии

•  На диаграмме рассеяния показаны не только точки-объекты и теоретическая линия регрессии, но и уравнение этой (прямой) линии:

Y = 8 . 761 e 4 + 2. 984 e 3 * X

•  Это уравнение записано в необычной форме, которая читается следующим образом:

Y = 87610 + 2984 X

Пример интерпретации коэффициента регресии

•  В уравнении Y = 87610 + 2984 X коэффициент регрессии равен +2984. Что это означает?

•  В данном случае смысл коэффициента регрессии состоит в том, что увеличение числа рабочих на 1 чел. приводит в среднем к увеличению объема годового производства на 2984 руб.

Свойства коэффициента регрессии

•  Коэффициент регрессии принимает любые значения.

•  Коэффициент регрессии не симметричен , т.е. изменяется, если X и Y поменять местами.

•  Единицей измерения коэффициента регрессии является отношение единицы измерения Y к единице измерения X ([ Y ] / [ X ]).

•  Коэффициент регрессии изменяется при изменении единиц измерения X и Y .

Пример единицы измерения коэффициента регрессии

•  В уравнении Y = 87610 + 2984 X коэффициент регрессии равен 2984. В каких единицах он измеряется?

•  Поскольку результативный признак Y измеряется в рублях, а факторный признак X в количестве рабочих (чел.), то коэффициент регрессии измеряется в рублях на человека (руб. / чел.)

 

Информационная Матрица Математическая энциклопедия информация по Фишер у,- матрица ковариаций информанта. Для доминированного семейства распределений вероятностей Pt(dw)с плотностями р(w; t), достаточно гладко зависящими от векторного (в частности, числового) параметра элементы И. м. при t= q определяются как где j, k=1, . .., т. При скалярном параметре tИ. м. описывается единственным числом - дисперсией информанта. И. м. I(q)определяет неотрицательную дифференциальную квадратичную форму снабжающую семейство римановой метрикой. Когда пространство Wисходов со конечно, Дифференциальная квадратичная форма Фишера (2) является единственной (с точностью до постоянного множителя) дифференциальной квадратичной формой, инвариантной относительно категории статистических решающих правил. Ввиду этого она возникает в формулировке многих статистич. закономерностей. Любое измеримое отображение f пространства Wисходов порождает новое гладкое семейство распределений Qt=Ptf-1 с И. м. IQ(q). При этом И; м. монотонно не возрастает: каковы бы ни были zl, ..., zm. И. м. обладает также свойством аддитивности. Если I(i)(q) (9) - И. м. для семейства с плотностью Р i((wi; t), то для семейства будет В частности, IN(q)=NI(q). при Nнезависимых одинаково распределенных испытаниях. И. м. позволяет охарактеризовать статистич. точность решающих правил в задаче оценки параметра закона распределения. Для дисперсии любой несмещенной оценки t(w)=т(w(1), ..., w(N)) скалярного параметра tсправедливо Аналогичное матричное неравенство информации выполняется для оценок векторного параметра. Его скалярное следствие показывает, что несмещенное оценивание нигде не может быть слишком точным. Для произвольных оценок последнее неверно. Однако остаются ограничения, напр., на среднюю точность где усреднение левой части (3) проведено по инвариантному объему Vлюбой компактной подобласти остаточный член зависит от размеров Q'. Неравенства (4) асимптотически точны, и асимптотически оптимальной в этом смысле оказывается оценка максимума правдоподобия. В точках вырождения, det I(q)=0, совместная оценка параметров затруднена; если det I(q) = 0 в нек-рой области, то совместная оценка вообще невозможна. Таким образом, следуя Р. Фишеру [1], с известной осторожностью можно сказать, что И. м. описывает среднее количество информации о параметрах закона раейределения, содержащееся в случайной выборке. Лит.:[1] Fisher R. А., "Ргос. Cambr. Phil. Soc", 1925, v. 22, p. 700-25; [2] Барра Ж.-Р., Основные понятия математической статистики, пер. с франц., М., 1974; [3] Ченцов Н. Н., Статистические решающие правила и оптимальные выводы, М., 1972. Н. Н. Чепцов.

11.Разностный метод решения краевых задач для уравнений 2-го порядка.Апроксимация производных. 12 Метод прогонки

13 Численное интегрирование. Базовые формулы численного интегрирования , алгоритм достижения заданной точности .

14. Метод ячеек для вычисления двойного интеграла.

2.2 Метод ячеек

Рассмотрим K-мерный интеграл по пространственному параллелепипеду . По аналогии с формулой средних можно приближённо заменить функцию на её значение в центральной точке параллелепипеда. Тогда интеграл легко вычисляется:

       (5)

Для повышения точности можно разбить область на прямоугольные ячейки (рис. 2). Приближённо вычисляя интеграл в каждой ячейке по формуле средних и обозначая через соответственно площадь ячейки и координаты её центра, получим:

                       (6)

Справа стоит интегральная сумма; следовательно, для любой непрерывной она сходится к значению интеграла, когда периметры всех ячеек стремятся к нулю

Оценим погрешность интегрирования. Формула (5) по самому её выводу точна для . Но непосредственной подстановкой легко убедиться, что формула точна и для любой линейной функции. В самом деле, разложим функцию по формуле Тейлора:

                       (7)

где , а все производные берутся в центре ячейки. Подставляя это разложение в правую и левую части квадратурной формулы (5) и сравнивая их, аналогично одномерному случаю легко получим выражение погрешности этой формулы:

                       (8)

ибо все члены разложения, нечётные относительно центра симметрии ячейки, взаимно уничтожаются

Пусть в обобщённой квадратурной формуле (6) стороны пространственного параллелепипеда разбиты соответственно на N 1 , N 2 , …, N k равных частей. Тогда погрешность интегрирования (8) для единичной ячейки равна:

Суммируя это выражение по всем ячейкам, получим погрешность обобщённой формулы:

       (9)

т.е. формула имеет второй порядок точности. При этом, как и для одного измерения, можно применять метод Рунге–Ромберга, но при одном дополнительном ограничении: сетки по каждой переменной сгущаются в одинаковое число раз.

Обобщим формулу ячеек на более сложные области. Рассмотрим случай K=2. Легко сообразить, что для линейной функции формула типа (5) будет точна в области произвольной формы, если под S подразумевать площадь области, а под –координаты центра тяжести, вычисляемые по обычным формулам:

                       (10)

Разумеется, практическую ценность это имеет только для областей простой формы, где площадь и центр тяжести легко определяется; например, для треугольника, правильного многоугольника, трапеции. Но это значит, что обобщённую формулу (6) можно применять к областям, ограниченным ломаной линией, ибо такую область всегда можно разбить на прямоугольники и треугольники

Для области с произвольной границей формулу (6) применяют иным способом. Наложим на область сетку из K-мерных параллелепипедов (рис.3). Те ячейки сетки, все точки которых принадлежат области, назовём внутренними ; если часть точек ячейки принадлежит области, а часть – нет, то назовём ячейку граничной . Объём внутренней ячейки равен произведению её сторон. Объёмом граничной ячейки будем считать объем той её части, которая попадает внутрь ; этот объём вычислим приближённо. Эти площади подставим в (6) и вычислим интеграл

Оценим погрешность формулы (6). В каждой внутренней ячейке ошибка составляет по отношению к значению интеграла по данной ячейке. В каждой граничной ячейке относительная ошибка есть , ибо центр ячейки не совпадает с центром тяжести входящей в интеграл части. Но самих граничных ячеек примерно в раз меньше, чем внутренних. Поэтому при суммировании по ячейкам общая погрешность будет , если функция дважды непрерывно дифференцируема; это означает второй порядок точности

Вычисление объёма граничной ячейки довольно трудоёмко, ибо требует определения положения границы внутри ячейки. Можно вычислять интегралы по граничным ячейкам более грубо или вообще не включать их в сумму (6). Погрешность при этом будет , и для хорошей точности потребуется более подробная сетка

Мы видели, что к области произвольной формы метод ячеек трудно применять; поэтому всегда желательно заменой переменных преобразовать область интегрирования в прямоугольный параллелепипед (это относится практически ко всем методам вычисления кратных интегралов)

15. Вычисление двойных интегралов редукцией к однократным методом трапеций.

Метод трапеций для оценки определенного интеграла. Величина определенного интеграла численно равна площади фигуры, образованной графиком функции и осью абсцисс (геометрический смысл определенного интеграла). Следовательно, найти  – это значит оценить площадь фигуры, ограниченной перпендикулярами, восстановленными к графику подынтегральной функции f(x) из точек a и b, расположенных на оси аргумента x.

Для решения задачи разобьем интервал [a,b] на n одинаковых участков. Длина каждого участка будет равна h=(b-a)/n (см. рис.).

Восстановим перпендикуляры из каждой точки до пересечения с графиком функции f(x). Если заменить полученные криволинейные фрагменты графика функции отрезками прямых, то тогда приближенно площадь фигуры, а следовательно и величина определенного интеграла оценивается как площадь всех полученных трапеций. Обозначим последовательно значения подынтегральных функций на концах отрезков f₀, f₁, f₂,..., f_n и подсчитаем площадь трапеций

В общем случае формула трапеций принимает вид

где f_i – значение подынтегральной функции в точках разбиения интервала (a,b) на равные участки с шагом h; f₀, f_n – значения подынтегральной функции соответственно в точках a и b.

Остаточный член пропорционален длине интервала [a,b] и квадрату шага h

Согласно рис. и формуле остаточного члена, точность вычисления определенного интеграла повышается с уменьшением шага h (увеличением числа отрезковn).

Метод трапеций можно реализовать в виде процедуры или даже функции, поскольку результат вычисления определенного интеграла – скалярная величина. Параметрами программного модуля являются границы интервала (a и b) и число шагов разбиения на малые интервалы n. Для составления универсальной функции целесообразно предусмотреть вычисление подынтегральной функции f(x) во внешней процедуре – функции.

{Вычисление определенного интеграла по формуле трапеций}

Function Integral (a,b:real; {Пределы интегрирования}

n : integer; {Число шагов}

f : mpd_func): real; {Имя функции, вычисляющей

подынтегральное выражение}

var

x, h, sum : real; i : integer;

begin

h := (b-a)/n;

sum := 0.0;

for i := 1 to n-1 do begin

x := a+i*h;

sum := sum + f(x);

end;

integral := h*((f(a)+f(b))/2+sum);

end {Integral};

Если подынтегральная функция на интервале [a,b] задана таблично в равноотстоящих узлах, то формула трапеций не изменяется: в формулу подставляются табличные значения f(x). При других вариантах табличного значения функции f(x) (неравноотстоящие узлы, точки a и b не совпадают с узлами таблицы), можно воспользоваться подходящим алгоритмом интерполирования табличной функции для приближенной оценки подынтегральной функции f(x) при произвольном значении аргумента x.

16.Метод Монте-Карло вычесления кратных интегралов, общая схема и алгоритм метода