Лекция 8. Нейронные сети. Типы нс. Обучение нс. Применение нс.

Рекуррентные нейронные сети

Рекуррентными нейронными сетями называются такие сети, в ко­торых выходы нейронных элементов последующих слоев имеют синаптические соединения с нейронами предшествующих слоев. Это приво­дит к возможности учета результатов преобразования нейронной сетью информации на предыдущем этапе для обработки входного вектора на следующем этапе функционирования сети. Рекуррентные сети могут использоваться для решения задач прогнозирования и управления.

Архитектура рекуррентных сетей

Существуют различные варианты архитектур рекуррентных ней­ронных сетей.

Сеть Джордана: В 1986 г. Джордан (Jordan) предложил рекур­рентную сеть (рис.8.1), в которой выходы нейронных элементов по­следнего слоя соединены посредством специальных входных нейронов с нейронами промежуточного слоя. Такие входные нейронные эле­менты называются контекстными нейронами (context units). Они рас­пределяют выходные данные нейронной сети на нейронные элементы промежуточного слоя.

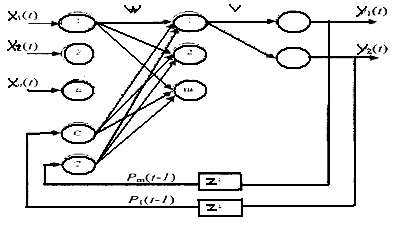
Рис. 8.1 Архитектура рекуррентной ней­ронной сети с обратными связями от нейро­нов выходного слоя

Число контекстных нейронов равняется числу выходных ней­ронных элементов рекуррентной сети. В качестве выходного слоя та­ких сетей используются нейронные элементы с линейной функцией активации. Тогда выходное значение j-го нейронного элемента последнего слоя определяется по формуле

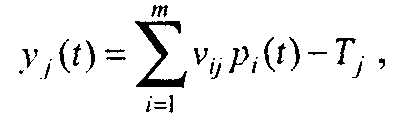(8.1)

где v_ij - весовой коэффи­циент между i-м нейроном промежуточного и j-м ней­роном выходного слоев; P_i(t)- выходное значение i-го нейрона промежуточ­ного слоя; t_j - пороговое значение j-го нейрона вы­ходного слоя. Взвешенная сумма i-гo нейронного элемента промежуточного слоя определяется следующим образом:

(8.2)

где w_ij – весовой коэффициент между j-м нейроном входного и i-м нейроном промежуточного слоев; р – число нейронов выходного слоя; w_ki – весовой коэффициент между k-м контекстным нейроном и i-м нейроном промежуточного слоя; T – пороговое значение i-го нейрона промежуточного слоя; n – размерность входно­го вектора.

Тогда выходное значение i-го нейрона скрытого слоя:

(8.3)

В качестве функции не­линейного преобразования F обычно используется гипер­болический тангенс или сигмоидная функция.

Для обучения рекуррентных нейронных сетей применяется алго­ритм обратного распространения ошибки (будет рассмотрен ниже).

Алгоритм обучения рекуррентной нейронной сети в общем слу­чае состоит из следующих шагов:

1. В начальный момент времени t = 1 все контекстные нейроны устанавливаются в нулевое состояние – выходные значения прирав­ниваются нулю.

2. Входной образ подается на сеть и происходит прямое распро­странение его в нейронной сети.

3. В соответствии с алгоритмом обратного распространения ошибки модифицируются весовые коэффициенты и пороговые значе­ния нейронных элементов.

4. Устанавливается t = t+1 и осуществляется переход к шагу 2. Обучение рекуррентной сети производится до тех пор, пока сум­марная среднеквадратичная ошибка сети не станет меньше заданной.

Рециркуляционные нейронные сети

Рециркуляционные сети характеризуются как прямым Y = f(X), так и обратным X = f(У) преобразованием информации. Задача тако­го преобразования – достижение наилучшего автопрогноза или само­воспроизводимости вектора X. Рециркуляционные нейронные сети применяются для сжатия (прямое преобразование) и восстановления исходной (обратное преобразование) информации. Такие сети явля­ются самоорганизующимися в процессе работы, где обучение произ­водится без учителя.

Архитектура рециркуляционной нейронной сети

Рециркуляционная нейронная сеть представляет собой совокупность двух слоев нейронных элементов, которые соединены между собой двунаправленными связями (рис.8.2).

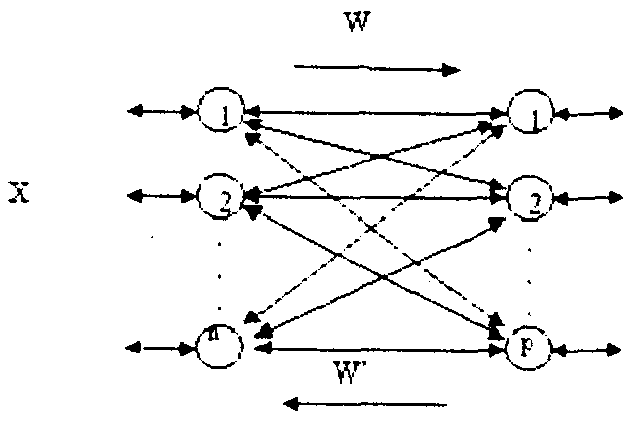
Рис.8.2 Архитектура рециркуляцион­ной нейронной сети

Каждый из слоев нейрон­ных элементов может использо­ваться в качестве входного или выходного. Если слой нейрон­ных элементов служит в качест­ве входного, то он выполняет распределительные функции. Иначе нейронные элементы слоя являются обрабатывающи­ми. Весовые коэффициенты, соответствующие прямым и обратным связям, характери­зуются матрицей весовых коэффициентов W и W'. Для наглядности рециркуляционную сеть можно представить в развер­нутом виде, как показано на рис.8.3.

Такое представление сети является эквивалентным и характеризует полный цикл преобразования информации. При этом промежуточный слой нейронных элементов производит кодирование (сжатие) входных данных X, а последний слой – восстановление сжатой информации Y. Слой нейронной сети, соответствующий матрице связи W, назовем пря­мым, а соответствующий матрице связей W' – обратным.

Рис. 8.3 Эквивалентное представление ре­циркуляционной сети

В качестве функции активации нейронных элементов F может использоваться как линейная, так и нелинейная функции.

Релаксационные НС

Релаксационные нейронные сети характеризуются прямым и обратным распро­странением информации между слоями нейронной сети. В основе функционирования лежит итеративный принцип работы. На каждой итерации процесса происходит обработка данных, полученных на предыдущем шаге. Такая циркуляция информации продолжается до тех пор, пока не установится состоя­ние равновесия. При этом состояния нейронных элементов перестают изменяться и ха­рактеризуются стационарными значениями.

Нейронные сети Хопфилда

Нейронная сеть Хопфилда реализует существенное свойст­во автоассоциативной памяти – восстановление по искаженному (зашумленному) образу ближайшего к нему эталонного. Входной вектор используется как начальное состояние се­ти, и далее сеть эволюционирует согласно своей динамике. При­чем любой пример, находящийся в области притяжения хранимого образца, может быть использован как указатель для его восста­новления. Выходной (восстановленный) образец устанавливается, когда сеть достигает равновесия.

Обучение сети Хопфилда производится по правилу Хебба.

Структура сети Хопфилда (рис.8.4) состо­ит из одного слоя нейронов, число которых определяет число вхо­дов и выходов сети. Выход каждого нейрона соединен с входами всех остальных нейронов. Выходные сигналы нейронов являются одновременно входными сигналами сети: Xi(k)=Yi(k-1)

Основные зависимости, определяющие сеть Хопфилда, можно представить в виде

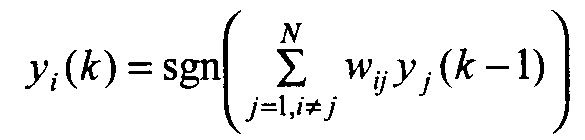(8.4)

с начальным условием y_i(0) = x_j. В процессе функционирования сети Хопфилда можно выделить два режима: обучения и классификации. В режиме обучения на основе известных обучающих выборок х подбираются весовые коэффициенты w_ij. В режиме классификации при зафиксированных зна­чениях весов и вводе конкретного начального состояния нейронов у(0) = х возникает переходный процесс, протекающий в соответствии с выраже­нием (Формула выше) и завершающийся в одном из локальных минимумов, для которого y(k) = y(k-l).

Для безошибочной работы сети Хопфилда число запоми­наемых эталонов N не должно превышать 0,15n (n-число нейронов).

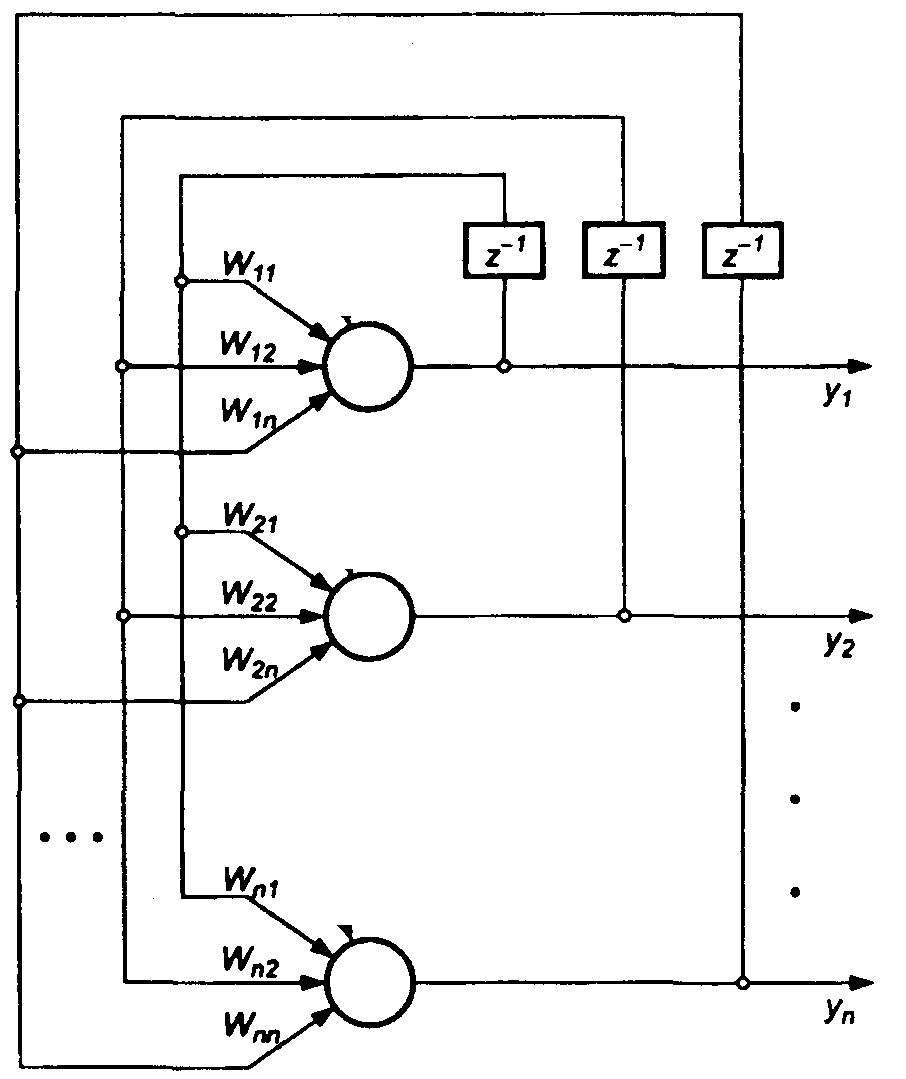
Рис. 8.4 Структура нейронной сети Хопфилда

ПОСТРОЕНИЕ НЕЙРОННОЙ СЕТИ

При построении модели ИНС прежде всего необходимо точ­но определить задачи, которые будут решаться с ее помощью. В настоящее время нейросетевые технологии успешно применяют­ся для прогнозирования, распознавания и обобщения.

Первым этапом построения нейросетевой модели является тщательный отбор входных данных, влияющих на ожидаемый ре­зультат. Из исходной информации необходимо исключить все сведения, не относящиеся к исследуемой проблеме. В то же вре­мя следует располагать достаточным количеством примеров для обучения ИНС. Существует эмпирическое правило, которое ус­танавливает рекомендуемое соотношение X между количеством обучающих примеров, содержащих входные данные и правиль­ные ответы, и числом соединений в нейронной сети: X <10.

Для факторов, которые включаются в обучающую выборку, целесообразно предварительно оценить их значимость, проведя корреляционный и регрессионный анализ, и проанализировать диапазоны их возможных изменений.

На втором этапе осуществляется преобразование исходных данных с учетом характера и типа проблемы, отображаемой ней­росетевой моделью, и выбираются способы представления ин­формации. Эффективность нейросетевой модели повышается, если диапазоны изменения входных и выходных величин приве­дены к некоторому стандарту, например [0,1] или [-1,1].

Третий этап заключается в конструировании ИНС, т.е. в проектировании ее архитектуры (число слоев и число нейронов в каждом слое). Структура ИНС формируется до начала обуче­ния, поэтому успешное решение этой проблемы во многом определяется опытом и искусством аналитика, проводящего ис­следования.

Четвертый этап связан с обучением сети, которое может проводиться на основе конструктивного или деструктивного подхода. В соответствии с первым подходом обучение ИНС на­чинается на сети небольшого размера, который постепенно уве­личивается до достижения требуемой точности по результатам тестирования. Деструктивный подход базируется на принципе «прореживания дерева», в соответствии с которым из сети с заве­домо избыточным объемом постепенно удаляют «лишние» ней­роны и примыкающие к ним связи. Этот подход дает возмож­ность исследовать влияние удаленных связей на точность сети. Процесс обучения нейронной сети представляет собой уточне­ние значений весовых коэффициентов для отдельных узлов на основе постепенного увеличения объема входной и выходной информации. Началу обучения должна предшествовать про­цедура выбора функции активации нейронов, учитывающая ха­рактер решаемой задачи. В частности, в трехслойных перцептронах на нейронах скрытого слоя применяется в большинстве слу­чаев логистическая функция, а тип передаточной функции ней­ронов выходного слоя определяется на основе анализа результа­тов вычислительных экспериментов на сети. Индикатором обу­чаемости ИНС может служить гистограмма значений межней­ронных связей.

На пятом этапе проводится тестирование полученной модели ИНС на независимой выборке примеров.

ОБУЧЕНИЕ НЕЙРОННЫХ СЕТЕЙ

Важнейшим свойством нейронных сетей является их способ­ность к обучению, что делает нейросетевые модели незаменимы­ми при решении задач, для которых алгоритмизация является не­возможной, проблематичной или слишком трудоемкой. Обучение нейронной сети заключается в изменении внутренних параметров модели таким образом, чтобы на выходе ИНС генерировался век­тор значений, совпадающий с результатами примеров обучающей выборки. Изменение параметров нейросетевой модели может вы­полняться разными способами в соответствии с различными алгоритмами обучения. Парадигма обучения определяется доступ­ностью необходимой информации. Выделяют три парадигмы:

• обучение с учителем (контролируемое);

• обучение без учителя (неконтролируемое);

• смешанное обучение.

При обучении с учителем все примеры обучающей выборки содержат правильные ответы (выходы), соответствующие исход­ным данным (входам). В процессе контролируемого обучения синаптические веса настраиваются так, чтобы сеть порождала отве­ты, наиболее близкие к правильным.

Обучение без учителя используется, когда не для всех приме­ров обучающей выборки известны правильные ответы. В этом случае предпринимаются попытки определения внутренней структуры поступающих в сеть данных с целью распределить об­разцы по категориям (модели Кохонена).

При смешанном обучении часть весов определяется посредст­вом обучения с учителем, а другая часть получается с помощью алгоритмов самообучения.

Обучение по примерам характеризуется тремя основными свойствами: емкостью, сложностью образцов и вычислительной сложностью. Емкость соответствует количеству образцов, кото­рые может запомнить сеть. Сложность образцов определяет спо­собности нейронной сети к обучению. В частности, при обуче­нии ИНС могут возникать состояния «перетренировки», в кото­рых сеть хорошо функционирует на примерах обучающей выбор­ки, но не справляется с новыми примерами, утрачивая способ­ность обучаться.

Рассмотрим известные правила обучения ИНС.

Правило коррекции по ошибке. Процесс обучения ИНС состо­ит в коррекции исходных значений весовых коэффициентов межнейронных связей, которые обычно задаются случайным об­разом. При вводе входных данных запоминаемого примера (сти­мула) появляется реакция, которая передается от одного слоя нейронов к другому, достигая последнего слоя, где вычисляется результат. Разность между известным значением результата и ре­акцией сети соответствует величине ошибки, которая может ис­пользоваться для корректировки весов межнейронных связей. Корректировка заключается в небольшом (обычно менее 1%) увеличении синаптического веса тех связей, которые усиливают правильные реакции, и уменьшении тех, которые способствуют ошибочным. Это простейшее правило контролируемого обуче­ния (дельта-правило) используется в однослойных сетях с одним уровнем настраиваемых связей между множеством входов и мно­жеством выходов.

Оптимальные значения весов межнейронных соединений можно определить путем минимизации среднеквадратичной ошибки с использованием детерминированных или псевдослу­чайных алгоритмов поиска экстремума в пространстве весовых коэффициентов. При этом возникает традиционная проблема оптимизации, связанная с попаданием в локальный минимум (будет рассмотрена ниже).

Правило Хебба. Оно базируется на следующем нейрофизи­ологическом наблюдении: если нейроны по обе стороны синапса активизируются одновременно и регулярно, то сила их синаптической связи возрастает. При этом изменение веса каждой меж­нейронной связи зависит только от активности нейронов, обра­зующих синапс. Это существенно упрощает реализацию алгорит­мов обучения.

Обучение методом соревнования. В отличие от правила Хебба, где множество выходных нейронов может возбуждаться одновре­менно, в данном случае выходные нейроны соревнуются (конкурируют) между собой за активизацию. В процессе сорев­новательного обучения осуществляется модификация весов свя­зей выигравшего нейрона и нейронов, расположенных в его окрестности («победитель забирает все»).

Рассмотрим один из наиболее распространенных алгоритмов обучения с учителем, относящийся к правилу коррекции по ошибке. Алгоритм обратного распространения ошибки

В многослойных нейронных сетях оптимальные выходные значения нейронов всех слоев, кроме последнего, как правило, неизвестны. Трех- или более слойный персептрон уже невозможно обучить, руководствуясь только величинами ошибок на выходах сети.

Один из вариантов решения этой проблемы – разработка наборов выходных сигналов, соответствующих входным, для каждого слоя нейронной сети, что, конечно, является очень трудоемкой операцией и не всегда осуществимо. Второй вариант – динамическая подстройка весовых коэффициентов синапсов, в ходе которой выбираются, как правило, наиболее слабые связи и изменяются на малую величину в ту или иную сторону, а сохраняются только те изменения, которые повлекли уменьшение ошибки на выходе всей сети. Очевидно, что данный метод, несмотря на кажущуюся простоту, требует громоздких рутинных вычислений. И, наконец, третий, более приемлемый вариант – распространение сигналов ошибки от выходов нейронной сети к ее входам, в направлении, обратном прямому распространению сигналов в обычном режиме работы. Этот алгоритм обучения получил название процедуры обратного распространения ошибки (error back propagation). Именно он рассматривается ниже.

Алгоритм обратного распространения ошибки – это итеративный градиентный алгоритм обучения, который используется с целью минимизации среднеквадратичного отклонения текущих от требуемых выходов многослойных нейронных сетей с последовательными связями.

Согласно методу наименьших квадратов, минимизируемой целевой функцией ошибки нейронной сети является величина:

(8.5)

где – реальное выходное состояние нейрона у выходного слоя нейронной сети при подаче на ее входы k-го образа; d_j,k – требуемое выходное состояние этого нейрона.

Суммирование ведется по всем нейронам выходного слоя и по всем обрабатываемым сетью образам. Минимизация методом градиентного спуска обеспечивает подстройку весовых коэффициентов следующим образом:

(8.6)

где w_ij – весовой коэффициент синаптической связи, соединяющей i-й нейрон слоя (q-1) с j-м нейроном слоя q; η – коэффициент ско­рости обучения, 0 < η <1.

В соответствии с правилом дифференцирования сложной функции:

, (8.7)

где s_j – взвешенная сумма входных сигналов нейрона j, т.е. аргумент активационной функции. Так как производная активационной функции должна быть определена на всей оси абсцисс, то функция единичного скачка и прочие активационные функции с неоднородностями не подходят для рассматриваемых нейронных сетей. В них применяются такие гладкие функции, как гиперболический тангенс или классический сигмоид с экспонентой (см. табл.7.1). Например, в случае гиперболического тангенса:

(8.8)

Третий множитель ∂s_j / ∂w_ij равен выходу нейрона предыдущего слоя .

Что касается первого множителя в (8.7), он легко раскладывается следующим образом:

(8.8)

Здесь суммирование по r выполняется среди нейронов слоя (q+1). Введя новую переменную

(8.9)

получим рекурсивную формулу для расчетов величин слоя q из величин более старшего слоя (q+1):

(8.10)

Для выходного слоя:

(8.11)

Теперь можно записать (8.6) в раскрытом виде:

(8.12)

Иногда для придания процессу коррекции весов некоторой инерционности, сглаживающей резкие скачки при перемещении по поверхности целевой функции, (8.12) дополняется значением изменения веса на предыдущей итерации:

(8.13)

где µ – коэффициент инерционности; t – номер текущей итерации.

Таким образом, полный алгоритм обучения нейронной сети с помощью процедуры обратного распространения строится следующим образом.

ШАГ 1. Подать на входы сети один из возможных образов и в режиме обычного функционирования нейронной сети, когда сигналы распространяются от входов к выходам, рассчитать значения последних. Напомним, что:

(8.14)

где L – число нейронов в слое (q-1) с учетом нейрона с постоянным выходным состоянием +1, задающего смещение; – i-й вход нейрона j слоя q.

(8.15)

где f(•)-сигмоид,

, (8.16)

где х_r – r-я компонента вектора входного образа.

ШАГ 2. Рассчитать δ^(Q) для выходного слоя по формуле (8.11).

Рассчитать по формуле (8.12) или (8.13) изменения весов ∆w^(Q) слоя Q (последнего слоя).

ШАГ 3. Рассчитать по формулам (8.10) и (8.12) соответственно δ^(Q) и ∆w^(Q) для всех остальных слоев, q = (Q – 1)…1.

ШАГ 4. Скорректировать все веса в нейронной сети:

(8.17)

ШАГ 5. Если ошибка сети существенна, перейти на шаг 1. В противном случае – конец.

Сети на шаге 1 попеременно в случайном порядке предъявляются все тренировочные образы, чтобы сеть, образно говоря, не забывала одни по мере запоминания других.

Из выражения (8.12) следует, что когда выходное значение стремится к нулю, эффективность обучения заметно снижается. При двоичных входных векторах в среднем половина весовых коэффициентов не будет корректироваться, поэтому область возможных значений выходов нейронов (0, 1) желательно сдвинуть в пределы (-0,5, 0,5), что достигается простыми модификациями логистических функций. Например, сигмоид с экспонентой преобразуется к виду:

(8.18)

Рассмотрим вопрос о емкости нейронной сети, т.е. числа образов, предъявляемых на ее входы, которые она способна научиться распознавать. Для сетей с числом слоев больше двух этот вопрос остается открытым. Для сетей с двумя слоями детерминистская емкость сети C_d оценивается следующим образом:

(8.19)

где L_w - число подстраиваемых весов, т - число нейронов в выходном слое.

Данное выражение получено с учетом некоторых ограничений. Во-первых, число входов n и нейронов в скрытом слое L должно удовлетворять неравенству (n+L) > m. Во-вторых, L_w/m > 1000. Однако приведенная оценка выполнена для сетей с пороговыми активационными функциями нейронов, а емкость сетей с гладкими активационными функциями, например (8.18), обычно больше. Кроме того, термин детерминистский означает, что полученная оценка емкости подходит для всех входных образов, которые могут быть представлены n входами. В действительности распределение входных образов, как правило, обладает некоторой регулярностью, что позволяет нейронной сети проводить обобщение и, таким образом, увеличивать реальную емкость. Так как распределение образов, в общем случае, заранее неизвестно, можно говорить о реальной емкости только предположительно, но обычно она раза в два превышает детерминистскую емкость.

Проблема локального минимума.

Рассматриваемая нейронная сеть имеет несколько «узких мест». Во-первых, в процессе большие положительные или отрицательные значения весов могут сместить рабочую точку на сигмоидах нейронов в область насыщения. Малые величины производной от логистической функции приведут в соответствии с (8.10) и (8.12) к остановке обучения, что парализует сеть ( ). Во-вторых, применение метода градиентного спуска не гарантирует нахождения глобального минимума целевой функции (в данном случае – функции ошибки). Находя на функции ошибки минимум, обучение останавливается. Но этот минимум по своему значению может быть слишком велик. Например, необходима ошибка в 0.01, а обучение остановилось на ошибке 0.1. Нужно искать глобальный минимум. Это тесно связано вопросом выбора скорости обучения. Приращения весов и, следовательно, скорость обучения для нахождения экстремума должны быть бесконечно малыми, однако в этом случае обучение будет происходить неприемлемо медленно, и с другой стороны, слишком большие коррекции весов могут привести к постоянной неустойчивости процесса обучения. Поэтому в качестве коэффициента скорости обучения η обычно выбирается число меньше 1 (например, 0,1), которое постепенно уменьшается в процессе обучения. Кроме того, для исключения случайных попаданий сети в локальные минимумы иногда, после стабилизации значений весовых коэффициентов, η кратковременно значительно увеличивают, чтобы начать градиентный спуск из новой точки. Если повторение этой процедуры несколько раз приведет сеть в одно и то же состояние, можно предположить, что найден глобальный минимум.

Обобщение и переобучение

Рассмотрим проблемы обобщения и переобучения нейронной сети более подробно. Обобщение – это способность нейронной сети делать точный прогноз на данных, не принадлежащих исходному обучающему множеству. Переобучение же представляет собой чрезмерно точную подгонку, которая имеет место, если алгоритм обучения работает слишком долго, а сеть слишком сложна для такой задачи или для имеющегося объема данных

Продемонстрируем проблемы обобщения и переобучения на примере аппроксимации некоторой зависимости не нейронной сетью, а посредством полиномов, при этом суть явления будет абсолютно та же.

Графики полиномов могут иметь различную форму, причем, чем выше степень и число членов, тем более сложной может быть эта форма. Для исходных данных можно подобрать полиномиальную кривую (модель) и получить, таким образом, объяснение имеющейся зависимости. Данные могут быть зашумлены, поэтому нельзя считать, что лучшая модель в точности проходит через все имеющиеся точки. Полином низкого порядка может лучше объяснять имеющуюся зависимость, однако, быть недостаточно гибким средством для аппроксимации данных, в то время как полином высокого порядка может оказаться чересчур гибким, но будет точно следовать данным, принимая при этом замысловатую форму, не имеющую никакого отношения к настоящей зависимости.

Емкость сети

Вопрос о емкости нейронной сети тесно связан с вопросом о требуемой мощности выходного слоя сети, выполняющего окончательную классификацию образов. Например, для разделения множества входных образов по двум классам достаточно одного выходного нейрона. При этом каждый логический уровень («1» и «0») будет обозначать отдельный класс. На двух выходных нейронах с пороговой функцией активации можно закодировать уже четыре класса. Для повышения достоверности классификации желательно ввести избыточность, путем выделения каждому классу одного нейрона в выходном слое или, что еще лучше, нескольких, каждый из которых обучается определять принадлежность образа к классу со своей степенью достоверности, например, высокой, средней и низкой. Такие нейронные сети позволяют проводить классификацию входных образов, объединенных в нечеткие (размытые или пересекающиеся) множества. Это свойство приближает подобные сети к реальным условиям функционирования биологических нейронных сетей.

ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ НЕЙРОСЕТЕВЫХ ТЕХНОЛОГИЙ

Применение нейросетевых технологий целесообразно при решении задач, имеющих следующие признаки:

• отсутствие алгоритмов решения задач при наличии достаточно большого числа примеров;

• наличие большого объема входной информации, характеризующей исследуемую проблему;

• зашумленность, частичная противоречивость, неполнота или избыточность исходных данных.

Нейросетевые технологии нашли широкое применение в таких направлениях, как распознавание печатного текста, контроль качества продукции на производстве, идентификация событий в ускорителях частиц, разведка нефти, борьба с наркотиками, медицинские и военные приложения, управление и оптимизация, финансовый анализ, прогнозирование и др.

В сфере экономики нейросетевые технологии могут использоваться для классификации и анализа временных рядов путем аппроксимации сложных нелинейных функций. Экспериментально установлено, что модели нейронных сетей обеспечивают большую точность при выявлении нелинейных закономерностей на фондовом рынке по сравнению с регрессионными моделями.

Рассмотрим решение задачи прогнозирования цены закрытия на завтра по акциям некоторого предприятия X. Для моделирования воспользуемся данными наблюдений за месяц. В качестве исходных данных можно использовать индикаторы Dow Jones, NIKKEI, FTSE100, индексы и акции российских компаний, «сезонные» переменные и др.

Относительный показатель однодневной доходности предприятия можно определить из соотношений:

(8.20)

где ∆P_i – оценка операции «вчера купил, сегодня продал»;

-∆P_i – оценка операции «вчера продал, сегодня купил»;

Р_i – значение выбранного показателя доходности в i-й день;

P_i-1 – значение показателя в (i-1)-й день.

Итоговая доходность за установленный интервал времени (n дней) рассчитывается по формуле

(8.21)

Результаты оценки доходности предприятия с использованием различных моделей ИНС, а также доходов «идеального» трейдера приведены ниже.

Индикаторы Доходность