Вопрос №15

В 1928 году академиком П.А. Ребиндером был установлен научный факт адсорбционного понижения прочности твердых тел вследствие уменьшения

поверхностной энергии, являющейся результатом физических или химических процессов на поверхности твердых тел (на поверхности трещин) [25, 37]. При этом происходит изменение механических свойств тела, приводящее к снижению прочности, возникновению хрупкости, уменьшению долговечности, понижению пластичности и т.д.

В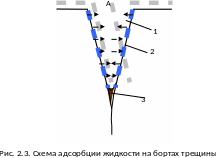 зазоре трещины в породе жидкость образует адсорбционный слой, на который действует давление в направлении дальнейшего продвижения в глубину микротрещины, способствуя, таким образом, её развитию, а значит разрушению породы (рис. 2.3).

• Адсорбция – (лат. ad – на, sorbeo – поглощаю) – поглощение веществ из растворов или газов на поверхности твердого тела или жидкости.

Вопрос №16

теория эффективных растягивающих нап-ряжений. Данная теория позволяет установить механизм формирования напряжений растяжения, касательных напряжений при нагружении породы усилием сжатия cо стороны внедряемого инструмента.

Интенсивность растягивающих напряжений во многом зависит от строения горной породы. В данном случае важными параметрами строения породы являются размер минеральных зерен и пористость.

Рассмотрим схемы (рис.2.5), на которых показан механизм возникновения растягивающих напряжений при внедрении твердого штампа в зернистую горную породу, смоделированную в виде набора шаров. Как следует из схем, центральные шары под внедряемым в породу штампом формируют область сжатия. Одновременно центральные шары, смещаясь вниз, вызывают перемещения боковых шаров в стороны и вверх. Эти, перемещаемые вверх, шары показывают направление развития растягивающих напряжений, под действием которых и происходит образование лунки разрушения породы при условии достаточной по величине нагрузке сжатия.

В данном случае большое значение на эффективность развития растягивающих напряжений оказывает размер зерен (шаров) и межзернового пространства.

При минимальном размере пор а≈0 (рис. 2.5, б), смещения зерен породы ограничены, поэтому будут развиваться деформации самих зерен, а порода проявлять более выраженные упругие характеристики.

Если размер пор значителен, и между зернами породы имеется пространство для смещений, то такая повышенная пористость обусловит увеличенный эффект деформации сжатия с минимальным развитием напряжений растяжения, поскольку прежде всего будет происходить смыкание порового пространства.

Особые условия развития деформаций и напряжений могут возникать, если поровое пространство заполнено жидкостью. В данном случае, как это уже рассмотрено, влияние порового пространства будет определяться соотношением порового и внешнего давлений.

Вопрос №17

В соответствии с теорией упругости под действием сосре-доточенной силы в упругом полупространстве возникают напря-жения, значения которых определяют по теории Буссинеска. При решении данной теоретической задачи прини-маются следующие допущения:

- в качестве объекта рассматривается упругое полу-пространство – упругое тело бесконечно больших размеров, ограниченное с одной стороны бесконечно большой плоскостью;

- площадь контакта внедряемого в упругое полупространство твердого тела (индентора) мала по сравнению с размерами упругого полупространства;

- горная порода представляется как однородное упругое изотропное тело;

- на породу действует только внешняя сила.

Основные положения теории Буссинеска

1. Если к упругому полупространству в точке О приложить сосредоточенную силу Р, перпендикулярно поверхности, то в твердом теле возникает напряженное состояние в объеме сферы (рис. 2.6).

2. В любой точке сферы (А, М, N) напряженное состояние тела характеризуется вектором σ, направленным к месту приложения сосредоточенной силы Р в точке О. Возникающее напряжение в виде суммы векторов σ, может быть представлено в виде нормального – σ_z и касательного – τ_zx.

3. В любой точке этой сферы (А, М, N) нормальное напряжение σ_z, параллельное оси OZ, будет иметь значение:

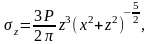(2.9)

где x, z - координаты точки, лежащей на окружности.

Касательное напряжение в этой точке соответственно определяется выражением

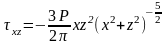. (2.10)

Полное напряжение σ, направленное из точки к месту приложения силы Р, будет иметь значение:

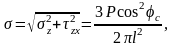(2.11)

где φ_с - угол между направлением действия силы Р и вектором полного напряжения;

l = ОА - расстояние от точки А до точки приложения силы Р.

И з треугольника ОАВ, вписанного в окружность, определим:

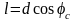. (2.12)

После этого получим выражение для расчета полного напряжения:

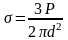. (2.13)

Выводы:

1. Из выражения (2.13) следует, что полное напряжение в любой точке сферы σ прямо пропорционально силе Р и обратно пропорционально расстоянию l и зависит от угла φ_с.

2. На любой горизонтальной площадке, расположенной в пределах поверхности сферы, имеющей диаметр d, полные напряжения σ одинаковы и имеют значения, вычисляемые по формуле (2.13).

Из формулы (2.13) также следует, что чем меньше диаметр сферы d, тем больше полное напряжение на ее поверхности. При бесконечно малом диаметре полное напряжение становится максимальным. Такие сферические напряжения называются сферами равных напряжений.

3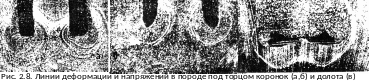 . Максимальным будет напряжение непосредственно в точке приложения вектора усилия Р.

4. Анализ полученных зависимостей показывает, что по оси симметрии Z действуют сжимающие напряжения, а на поверхности полупространства имеет место чистый сдвиг.

При d →0 , напряжение σ_z→∞. Следовательно, сжимающие напряжения на поверхности из вышеприведенных формул определить нельзя.

Согласно принципу Б. Сен-Венана, сосредоточенную силу Р можно заменить эквивалентной ей распределенной нагрузкой Р_р по кругу радиуса а. В этом случае нормальные напряжения определяются на любом расстоянии от поверхности следующей формулой:

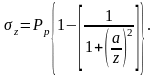(2.14)

Действительно, при z=0 σ_z=P_p; при z→∞ σ_z→0.

И ллюстрацией линий равных напряжений могут служить круги на воде, расходящиеся от брошенного в воду камня, сферы равных напряжений, зафиксированные при внедрении резца в твердое тело (рис. 2.7) или линии деформации в породе, полученные Е.И. Быченковым (рис. 2.8)

В том случае, если сила Р будет приложена к поверхности породы под углом, то напряжения в массиве распространяются в виде деформированных сфер, форма которых близка к овалу или эллипсу. Разрушение же породы (выкалывание лунки) произойдет в направлении ближайшей свободной поверхности (по направлению действующей силы), что приведет к формированию асимметричной лунки разрушения (рис. 2.9).