СОДЕРЖАНИЕ

Введение 8

1 Раздел 1. Расчет сложной электрической цепи постоянного тока 8

1.1 Расчет токов по законам Кирхгофа 8

1.2 Замена треугольника сопротивлений эквивалентной звездой 8

1.3 Расчет методом «Контурных токов» 8

1.4 Баланс мощностей электрической цепи 8

1.5 Расчет потенциалов точек электрической цепи 8

2 Раздел 2. Расчет и анализ электрической цепи переменного тока 8

2.1 Расчет токов комплексным методом 8

2.2 Определение активной мощности ваттметра 8

2.3 Баланс активной и реактивной мощностей 8

2.4 Векторная диаграмма токов 8

3 Раздел 3. Расчет трехфазной электрической цепи 8

3.1 Расчет фазных и линейных токов 8

3.2 Мощности трехфазной электрической цепи 8

3.3 Векторная диаграмма токов и напряжений 8

4 Раздел 4. Расчет трехфазного асинхронного двигателя 8

Заключение 8

Список использованной литературы 8

Введение

Высокие темпы промышленного производства и социального прогресса требуют резкого увеличения выработки тепловой энергии на базе мощного развития топливно-энергетического комплекса страны. Централизованные системы теплоснабжения от тепловых электрических станций (ТЭС) наиболее эффективны. В настоящее время, централизованное теплоснабжение крупных городов осуществляется на базе мощных атомных станций теплоснабжения.

Раздел 1. Расчет сложной электрической цепи постоянного тока

Параметры схемы приведены в таблице 1.

Таблица 1 – Параметры схемы электрической цепи.

ЭДС источника питания 1 (E1)	8 В
ЭДС источника питания 2 (E2)	6 В
ЭДС источника питания 3 (E3)	36 В
Внутреннее сопротивление источника питания (R01)	0,2 Ом
Внутреннее сопротивление источника питания (R02)	0,2 Ом
Внутреннее сопротивление источника питания (R03)	0,2 Ом
Сопротивление резистора 1 (R1)	8 Ом
Сопротивление резистора 2 (R2)	9 Ом
Сопротивление резистора 3 (R3)	2 Ом
Сопротивление резистора 4 (R4)	6 Ом
Сопротивление резистора 5 (R5)	3 Ом
Сопротивление резистора 6 (R6)	5 Ом

1. Расчет токов по законам Кирхгофа

Показываем на схеме направление токов в ветвях (рис. 1).

Согласно первому закону Кирхгофа для цепей постоянного тока алгебраическая сумма токов в любом узле электрической цепи равна нулю, т.е. сумма токов, направленных от узла, равна сумме токов, направленных к узлу.

Составляем уравнения по первому закону Кирхгофа для узлов, количество которых равно (n–1), где n – количество узлов в схеме:

А) –I₁ – I₂ – I₃ = 0; (1.1)

B) I₁ – I₄ + I₅ = 0; (1.2)

C) I₂ + I₄ + I₆ = 0. (1.3)

Согласно второму закону Кирхгофа для цепей постоянного тока в любом замкнутом контуре алгебраическая сумма напряжений на резистивных элементах равна алгебраической сумме ЭДС.

Составляем уравнения по второму закону Кирхгофа для каждого контура:

1. –I₁ ∙ (R₁ + R₀₁) + I₂ ∙ (R₂ + R₀₂) – I₄ ∙ R₄ = –E₁ + E₂; (1.4)

2. I₁ ∙ (R₁ + R₀₁) – I₃ ∙ (R₃ + R₀₃) – I₅ ∙ R₅ = E₁ – E₃; (1.5)

3. I₄ ∙ R₄ + I₅ ∙ R₅ – I₅ ∙ R₅ = 0. (1.6)

Решаем все полученные уравнения совместно как систему, подставив все известные значения:

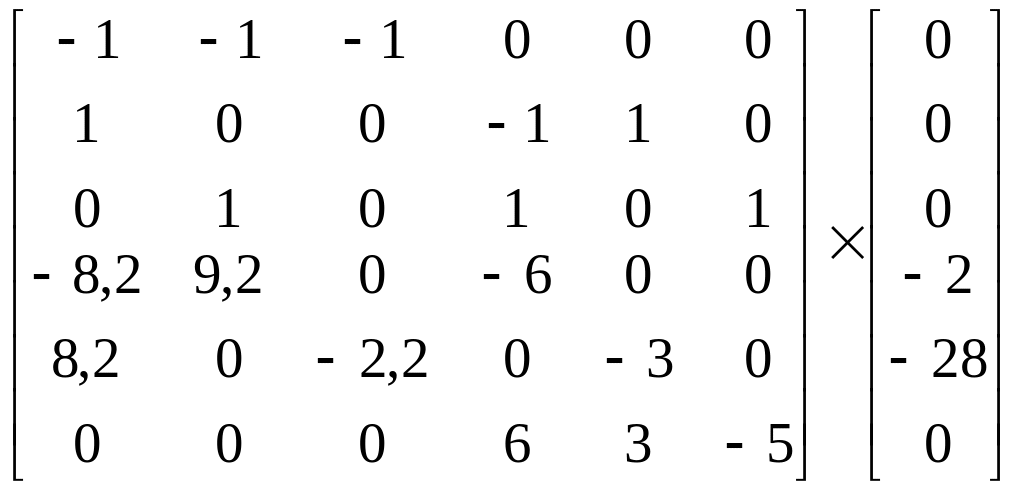=> (1.7)

Решив матрицу, получим неизвестные значения токов в ветвях:

I₁ = 1,77 А;

I₂ = 1,65 А;

I₃ = 3,42 А;

I₄ = 0,21 А;

I₅ = 1,98 А;

I₆ = 1,44 А.

Если ток в ветви оказался отрицательным, значит, его направление противоположно выбранному на схеме.

2. Замена треугольника сопротивлений эквивалентной звездой

Проведем преобразование «треугольника» bcd, соответствующего схеме электрической цепи, в эквивалентную «звезду» (рис. 2). Исходный треугольник образован сопротивлениями R₄, R₅, R₆. При преобразовании обязательно сохраняется условие эквивалентности схем, т.е. токи в проводах, проходящих к преобразуемой схеме, и напряжения между узлами не меняют своих величин.

При преобразовании «треугольника» в «звезду» используем расчетные формулы:

Ом; (1.8)

Ом; (1.9)

Ом. (1.10)

В результате преобразования исходная схема упрощается (рис. 3).

В преобразованной схеме только три ветви и соответственно три тока I₁, I₂, I₃. Для расчета этих токов достаточно иметь систему трех уравнений, составленных по законам Кирхгофа:

(1.11)

При составлении уравнений направление тока и обхода контуров выбирается так же, как и в трехконтурной схеме.

Составляем и решаем матрицу:

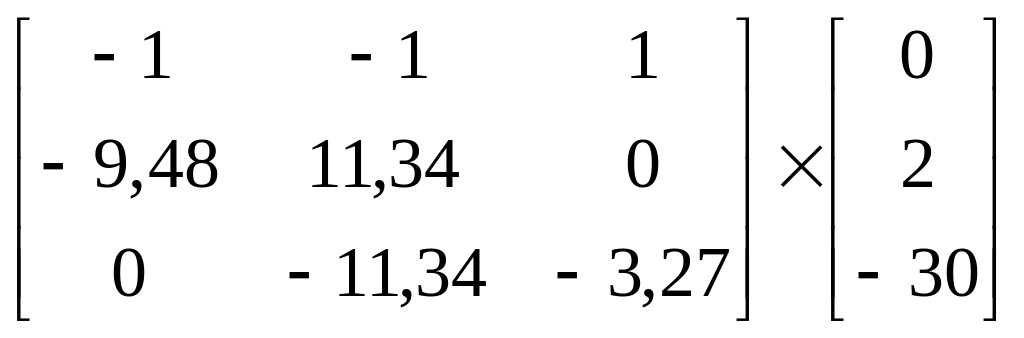(1.12)

Решив матрицу, получим неизвестные значения токов I₁, I₂, I₃:

I₁ = 1,77 А;

I₂ = 1,65 А;

I₃ = 3,42 А.

Подстановкой полученных значений токов в уравнения, составленные для трехконтурной схемы, определим остальные токи I₄, I₅, I₆:

I₄ = 0,21 А;

I₅ = 1,98 А;

I₆ = 1,44 А.