49.Изобр-е в pv и ts-диаграммах тд-ких процессов, протекающих в многоступенчатых компрессорах.

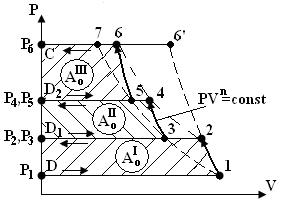
Рис. 6.2. Теоретическая индикаторная диаграмма3-х ступенчатого компрессора

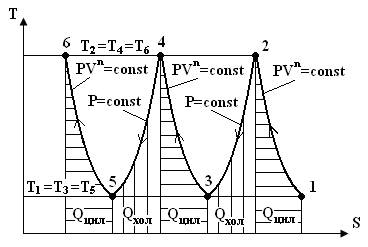
Рис. 6.3. Процесс сжатия в T-S диаграмме3-х ступенчатого компрессора

50.Опр-е отношения давления (относительного повышения давления) в ступенях многост-ого Компрессора

Из условия :Для I ступени ;Для IIрой: ;Для IIIтей:

Но так как n=const(n-политропы сжатия) и Т₁=Т₃=Т₅, а Т₂=Т₄=Т₆, то правые части одинаковы => равны и левые: (*)

z – Отношение давлений в каждой ступени

Если записать как: (*)

то Р₂, Р₃, Р₄, Р₅ сократятся, т.к. Р₂ =Р₃, Р₄=Р_5.Откуда

В общем случае для m – ступенчатого компрессора:

Найдем увеличение давления по ступеням в отношении к :Из Ур-я (*):

;

,где: i - № ступени.

Т.о давл-е сжатого газа по ступеням увел-ся по отношению к Рнач=Р₁ по закону геометр-ой прогрессии со знаменателем Z.

51.Объемы цилиндров многост-ого поршневого компрессора.

Т.к. точки 1, 3, 5 находятся на одной изотерме (Т₁=Т₃=Т₅) , то

Откуда : ; ,Здесь: Р₃=Р₂ и Р₅=Р₄.

Т.о. V₁, V₅, V₃ образуют уменьш-ся геометр-ю прогрессию со знаменателем :

V₂, V₄, V₆ , т.е. объемы в конце сжатия соответ-щей ступени, опр-ся из ур-ний политропы:

P₁V₁ⁿ= P₂V₂ⁿ  ,

Лоренца в PV- диаграмме

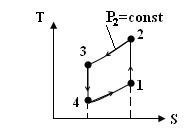
Рис.2.1. Цикл Рис.2.2. Цикл Лоренца в TS – диаграмме

т.к. P₂V₂= P₄V₄= P₆V₆ из условия Т₂=Т₄=Т₆, то

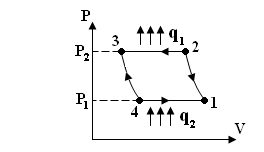
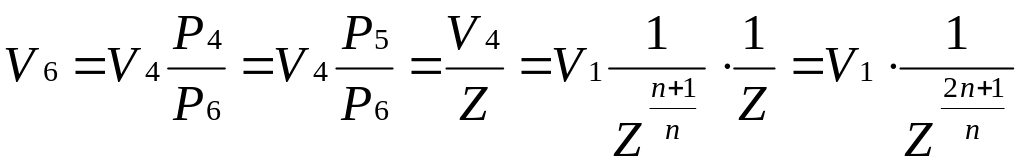
55.Обратный цикл Карно.Холодильный коэф-т идеальной холодильной установки.

Идеальным циклом ХУ яв-ся обратный обратимый цикл Карно(рис.1).

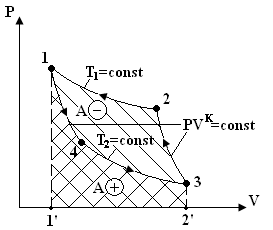
Рис. 1.1. Обратный обратимый цикл Карно в PV – диаграмме

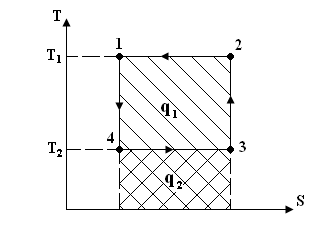
Рис. 1.2. Обратимый цикл Карно в TS– диаграмме

(1 – 4)адиаб-е расширение

(4 – 3) изотер-ое расш-е с отбором теплоты q₂ от холодного источника Т₂

(3 – 2) адиаб-ое сжатие

(2 – 1) изотер-ое сжатие с отдачей теплоты q₁ горяч.источнику Т₁

Работа отрицательна (см. рис. 1), т.к. площадь под кривой 1-4-3 (А⁺) меньше, чем площадь под кривой 3-2-1 (А^–). Т. к. в круговом процессе ∆U=0, то в соотв-вии с I началом ТД затрач-ая работа равна:

Холодильный коэффициент – отношение отведенной от охлаждаемого тела теплоты q2 (произведенного холода) к затраченной работе (l_ц=q₁–q₂).

-для 1 кг холодильного агента

Для обратного цикла Карно ε имеет max значение:

не зависит от вида рабочего тела

Отношение характеризует степень совершенства принимаемого цикла.

1)Холодильный агент – рабочее тело холодильной машины.

2)Холодопроизводительность (Q_т) – это кол-во теплоты, которое отводится от охлаж-ого тела в ед. времени Q [Дж/сек].

Работа холод-й устан-ки в ед.времени:

[кВт]

56. Цикл воздушной холодильной установки (ВХУ). Холодильный коэффициент ВХУ.

Цикл Лоренца – это цикл, состоящий из двух изобар и адиабат.

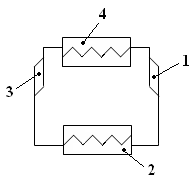
Рис.2.3. Принципиальная схема ВХУ:

1 – компрессор; 2–рефрижератор (охлаждаемое помещение);3–детандер (расширительный цилиндр);4–охладитель (холодильник)

Процессы в компрессоре и детандере считаются адиаб-ми, в конденсаторе и рефрижераторе – изобарными

Теплота отдаваемая окр.среде в конденсаторе при Р₂=const (процесс 2-3).

– на 1 кг воздуха

Теплота отбираемая в рефрижераторе

– на 1 кг воздуха

Работа, необходимая на осущес-ие цикла:

- на 1кг воздуха

Холодильный коэффициент: Для адиабатных процессов (1-2) и (3-4) можно записать:

Т.о, холодильный коэф-т ВХУ зависит только от отношения давлений.

Обратный обратимый цикл Карно и цикл Лоренца в TS– диаграмме

Из рис.видно,что в обратном цикле Карно удельная холодопроиз-ность q₂ больше, чем в цикле Лоренца,а работа, затрачивается на цикл Карно меньше. Таким образом, ε_{лоренца}< ε_карно.