Бесконечно малая величина
Последовательность 
называется бесконечно
малой,
если 
.
Например, последовательность чисел 
—
бесконечно малая.
Функция
называется бесконечно
малой в окрестности точки 
,
если 
.
Функция
называется бесконечно
малой на бесконечности,
если 
либо 
.
Также
бесконечно малой является функция,
представляющая собой разность функции
и её предела, то есть если 
,
то 
, 
.
Свойства бесконечно малых
Сумма конечного числа бесконечно малых — бесконечно малая.
Произведение бесконечно малых — бесконечно малая.
Произведение бесконечно малой последовательности на ограниченную — бесконечно малая. Как следствие, произведение бесконечно малой на константу — бесконечно малая.
Если — бесконечно малая последовательность, сохраняющая знак, то
— бесконечно
большая последовательность.
Определение. Предел функции f(x) при ха, где а- число, равен бесконечности, если для любого числа М>0 существует такое число >0, что неравенство
выполняется при всех х, удовлетворяющих условию
Записывается 
.
[an error occurred while processing this directive]
Собственно, если в приведенном выше определении заменить условие f(x)>M на f(x)>M, то получим:
а если заменить на f(x)<M, то:
Графически приведенные выше случаи можно проиллюстрировать следующим образом:
|
|
|
|
Определение. Функция
называется бесконечно
большой при
ха,
где а – чосли или одна из величин ,
+ или
-,
если 
,
где А – число или одна из величин ,
+ или
-.
Связь бесконечно больших и бесконечно малых функций осуществляется в соответствии со следующей теоремой.
Теорема. Если f(x)0 при ха (если х ) и не обращается в ноль, то
Французский математик Лагранж более 100 лет назад доказал, что всякое натуральное число может быть представлено в виде суммы не более 4 квадратов натуральных чисел. Возник вопрос: сколько надо k-тых степеней натуральных чисел, чтобы представить их суммой всякое натуральное число. Эту проблему поставил английский математик Варинг.
6)
(о
связи функции с ее пределом). Для того
чтобы 
необходимо
и достаточно выполнение равенства
где
—
б.м. при х
а
—
б.м.,
х
а)
Запишем цепочку равносильных утверждений, следующих из определения предела функции и определения б.м.:
Предел
суммы конечного числа функций, имеющих
пределы при х
а,
равен сумме их пределов
Пусть
тогда
по теореме 2 име-
ем
где
—
б.м. при
х
а,
следовательно,
Используя
лемму 1 о б.м., заключаем, что
—
б.м. при
и
по теореме 2 получаем равенство
b1
+ b2
Пусть функции u = u(x) и v = v(x) имеют в точке x0. Тогда в этой точке имеют производные их сумма, произведение и, при дополнительном условии v(x0) ≠ 0, их частное, причем:
7)
Не
всякая функция имеет предел, даже
будучи ограниченной.
Например, sin x при x предела
не имеет, хотя Укажем два признака существования предела функции. Теорема (о промежуточной функции).
Пусть
в некоторой окрестности О (а)
точки а функция f(x) заключена
между двумя функциями (x)
и (x),
имеющими одинаковый предел А при x a,
то есть (x) f(x)
Тогда
функция f(x) имеет
тот же предел: Функция f (x) называется возрастающей на данном множестве X, если f(x1)<f(x2) для x1< x2 (x1, x2 X).
Функция f(x) называется убывающей на
множестве X,
если f( Возрастающая или убывающая функция называется монотонной на данном множестве X.
Если f(
) f( Теорема.
Пусть функция f(x) монотонна
и ограничена при x a (или
при x a).
Тогда существует соответственно |
|
1.
(x)
и 
)
> f(x2) для x1< x2 (x1, x2 X).
) для x1< x2,
то f(x) называют
неубывающей, а если f(x1) f(x2) для x1< x2 –
не возрастающей. И в этом случае
функцию называют монотонной.
(или 
).1 замечательный предел.
Возьмем круг радиуса 1, обозначим
радианную меру угла MOB через Х.
Пусть 0 < X < π/2. На рисунке |АМ| = sin x, дуга МВ численно равна центральному углу Х, |BC| = tg x. Тогда
Разделим
все на
и
получим:
Т.к.
,
то по признаку существования пределов
следует
.
2 замечательный предел.
Пусть х→∞. Каждое значение х заключено между двумя положительными целыми числами:
Если x→∞, то n→∞, тогда
По признаку о существовании пределов:
8)
Пусть 
--
некоторая функция, 
--
её область определения и 
--
некоторый (открытый) интервал (может
быть, с 
и/или 
)7.
Назовём функцию
непрерывной
на интервале 
,
если
непрерывна
в любой точке 
,
то
есть для любого
существует 
(в
сокращённой записи:
Пусть
теперь 
--
(замкнутый) отрезок в
.
Назовём функцию 
непрерывной
на отрезке
,
если
непрерывна
на интервале
,
непрерывна справа в точке 
и
непрерывна слева в точке 
,
то есть
9) Точка разрыва - значение аргумента, при котором нарушается непрерывность функции (см. Непрерывная функция). В простейших случаях нарушение непрерывности в некоторой точке а происходит так, что существуют пределы
при стремлении x к а справа и слева, но хотя бы один из этих пределов отличен от f (a). В этом случае а называют Точкой разрыва 1-го рода. Если при этом f (a + 0) = f (a —0), то разрыв называется устранимым, так как функция f (x) становится непрерывной в точке а, если положить f (a)= f(a+0)=f(a-0).
Разрывные функции, функции, имеющие разрыв в некоторых точках (см. Разрыва точка). Обычно у функций, встречающихся в математике, точки разрыва изолированы, но существуют функции, для которых все точки являются точками разрыва, например функция Дирихле: f (x) = 0, если х рационально, и f (x) = 1, если х иррационально. Предел всюду сходящейся последовательности непрерывных функций может быть Р. ф. Такие Р. ф. называются функциями первого класса по Бэру.
10) Свойства функций, непрерывных на отрезке
Теорема 1 (об ограниченности непрерывной функции). Если функция f(x) непрерывна на отрезке [a, b], то она ограничена на этом отрезке, т.е. существует такое числоC> 0, что x [a, b] выполняется неравенство |f(x)| ≤ C.
Теорема 2 (Вейерштрасс). Если функция f(x) непрерывна на отрезке [a, b], то она достигает на этом отрезке своего наибольшего значения M и наименьшего значения m, т.е. существуют точки α, β [a, b] такие, что m = f(α) ≤ f(x) ≤ f(β) = M для всех x [a, b] (рис.2).
Наибольшее значение M обозначается символом maxx [a, b] f(x), а наименьшее значение m — символом minx [a, b] f(x).
Теорема 3 (о существовании нуля). Если функция f(x) непрерывна на отрезке [a, b] и на концах отрезка принимает ненулевые значения разных знаков, то на интервале(a, b) найдется по крайней мере одна точка ξ в которой f(ξ) = 0.
Геометрический смысл теоремы состоит в том, что график функции, удовлетворяющей условиям теоремы, обязательно пересечет ось OX (рис.3).
Замечание. На этой теореме основан метод приближенного решения уравнения f(x) = 0,
называемый методом бисекции (дихотомии), или методом половинного деления.
Теорема Вейерштрасса
Пусть
f — непрерывная функция, определённая
на отрезке [a,b]. Тогда для любого
существует такой многочлен p с
вещественными коэффициентами, что для
любого x из
выполнено условие
Теорема Больцано — Коши
Пусть
дана непрерывная функция на отрезке
Пусть также
и без ограничения общности предположим,
что
Тогда для любого
существует
такое, что f(c) = C.
11) Как известно, сумма, разность и произведение двух б.м.ф. есть функция бесконечно малая. Отношение же двух б.м.ф. может вести себя различным образом: быть конечным числом, быть бесконечно большой функцией, бесконечно малой или вообще не стремиться ни к какому пределу.
Две б.м.ф. сравниваются между собой с помощью их отношения.
Пусть α=α(х) и ß=ß(х) есть б.м.ф. при х→хо, т. е.
и 
1.
Если 
=А 0
(АєR), то α и ß называются бесконечно
малыми одного порядка.
2. Если, =0, то α називатся бесконечно малой более высокого порядка , чем ß.
3. Если =∞, то α называется бесконечно малой более низкого порядка, чем ß.
4. Если не существует, то α и ß называются несравнимыми бесконечно малыми.
Среди бесконечно малых функций одного порядка особую роль играют так называемые эквивалентные бесконечно малые.
Если 
то
α и ß называются эквивалентными
бесконечно малыми (при
х→x0);
это обозначается так: α~ß.
Например,
sinx~х при х→0, т.к 
при
x→0, т. к. 
Теорема 18.1 . Предел отношения двух бесконечно малых функций не изменится, если каждую или одну из них заменить эквивалентной ей бесконечно малой.
Теорема 18.2 . Разность двух эквивалентных бесконечно малых функций есть бесконечно малая более высокого порядка, чем каждая из них.
Справедливо и обратное утверждение: если разность б.м.ф. α и ß есть бесконечно малая высшего порядка, чем α или ß, то α и ß — эквивалентные бесконечно малые.
Действительно, так как
т.
е. 
Отсюда 
т. е. α~ß. Аналогично, если
то
α~ß.
Теорема 18.3 . Сумма конечного числа бесконечно малых функций разных порядков эквивалентна слагаемому низшего порядка.
Докажем
теорему для двух функций. Пусть α→0,
ß→0 при х→хо,
причем α — б.м.ф. высшего порядка, чем
ß, т. е. 
.
Тогда
Следовательно, α+ß~ß при х→х0.
Слагаемое, эквивалентное сумме бесконечно малых, называется главной частью этой суммы.
Замена суммы б.м.ф. ее главной частью называется отбрасыванием бесконечно малых высшего порядка.
Эквивалентные величины
Если 
,
то бесконечно малые
величины 
и 
называются эквивалентными (
).
Очевидно, что эквивалентные величины являются частным случаем бесконечно малых величин одного порядка малости.
При 
справедливы
следующие соотношения эквивалентности
(как следствия из так называемых замечательных
пределов):
,
где 
;
,
где
;
,
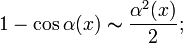
поэтому используют выражение:
,
где
.
ТеоремаПредел частного (отношения) двух бесконечно малых величин не изменится, если одну из них (или обе) заменить эквивалентной величиной.Данная теорема имеет прикладное значение при нахождении пределов (см. пример).
12) Производной функции y=f(x) в точке х0 называется предел отношения приращения функции к приращению аргумента, когда аргумент стремится к нулю.
Геометрический смысл производной. Производная в точке x0 равна угловому коэффициенту касательной к графику функции y=f(x) в этой точке.
уравнение
касательной к графику функции y=f(x) в
точке x0 :
Физический смысл производной.
Если
точка движется вдоль оси х и ее координата
изменяется по закону x(t), то мгновенная
скорость точки:
13) Производная функции f(x) есть некоторая функция
f ’(x), произведенная из данной функции.
Функция y=f(x), имеющая производную в каждой точке интервала (a;b) называется дифференцируемой в этом интервале.
Операция нахождения производной называется дифференцированием.
Дифференциал функции y=f(x) в точке х называется главная часть ее приращения, равная произведению производной функции на приращение аргумента, и обозначается dy (или df(x) ).
Иначе. Дифференциал функции равен произведению производной этой функции на дифференциал независимой переменной.
Ответ на первый вопрос: из непрерывности функции не следует ее дифференцируемость.
Ответ на второй вопрос: из дифференцируемости функции следует ее непрерывность.
Рассмотрим более конкретно каждый вопрос. Чтобы ответить на данные вопросы необходимо доказать озвученый факт или привести пример, который опровергает этот факт.
Найдем
производную следующей функции 
.
Хорошо известно, данная функция является
непрерывной и, что ее производная будет
следующей:
Покажем, что в точке нуль производная не существут. Для этого найдем производную в нуле по определению производной:
данный
предел равен 1, если 
и
равен (-1), если 
,
получаем, что предел не существует,
следовательно в нуле производной нет
и функция в нуле не дифференцируема.
14)
Правила
дифференцирования суммы, произведения,
частного функции. Производные сложных
функций.
Для нахождения производной сложной
функции надо производную данной функции
по промежуточному аргументу умножить
на производную промежуточного аргумента
по независимому аргументу.
15)
Логарифмическое дифференцирование -
в некоторых
случаях целесообразнее функцию сначала
прологарифмировать, а результат
продифференцировать.
Однако производные степенных функций находят только логарифмическим дифференцированием.
Производная
степенно-показательной функции равна
сумме производно показательной функции,
при условии U=const,
и производной степенной функции, при
условии V=const.
16)
призводная
элементарных функций
17) Производная обратной функции равна обратной величине производной данной функции.
Теорема.
Пусть функция 
определена
на промежутке Х,
непрерывна, монотонна (возрастает или
убывает) и дифференцируема на Х.
Если ее производная 
в
точке 
не
равна нулю, то обратная
функция 
имеет
производную 
в
точке 
,
причем
. (4.1)
Доказательство.
Функция
определена,
непрерывна и монотонна на промежутке Х,
тогда она имеет обратную функцию 
,
определенную, непрерывную и монотонную
на промежутке Y.
Если
значение аргумента 
получает
приращение 
,
отличное от нуля, то в силу монотонности
функции
функция 
получает
приращение 
и 
.
В силу непрерывности функции 
: 
.
Следовательно, 
Итак, 
Теорема доказана.
Свойства
взаимно обратных функций 
и 
.
1
и 
2Из первого свойства видно, что область определения функции совпадает с областью значений функции и наоборот.
3Графики взаимно обратных функций симметричны относительно прямой y=x .
4Если возрастает, то и возрастает, если убывает, то и убывает.
18)
Дифференцирование обратных тригонометрических функций |
|
|
|
Функция
Учитывая, что
получим
Таким образом,
Учитывая, что
получим
|
является обратной для функции 
.
Следовательно,
является обратной для функции 
.
Тогда
Аналогично,
Тогда
Поскольку
то
Подобным
образом выводится формула
дифференцирования функции 
: