12. Закон Лапласа: общая форма, частные случаи, капиллярное поднятие жидкости, уравнение Жюрена.

Вследствие избыточной пов-й энергии подвешенная жидкость в условии невесомости приобретает сферическую форму. С уменьшением кол-ва жидкости роль силы тяжести снижается, т.к. она уменьшается пропорц-но кубу, а пов-ть квадрату радиуса тела, т.е. увеличивается удельная пов-ть . С появлением кривизны пов-ти тела радиусом r возникает дополнительное внутреннее давление дельта Р .Его можно представить как равнодейств. силу пов-го натяжения ,сходящихся в одной точке. Равнодейсв. направлена перпендикулярно пов-ти в центр кривизны.

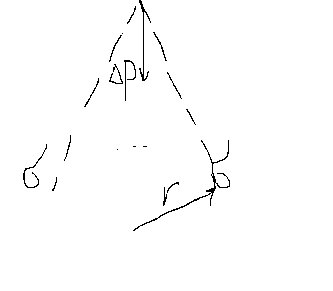
Эта сила рассчитана на ед площади и представляет собой доп-е давление:

Где Δ Р - разность давлений внутри тела с изогнутой и плоской пов-ти. - кривизна поверхности. Чем больше σ, тем влияние кривизны значительное для сферической формы.

Для цилиндрической пов-ти длиной L и радиусом r имеем: Тогда:

для пов-ти неправильной формы используется представление средней кривизны, опред. по уравнению: Где 1/r₁ и 1/r₂ -кривизна главных нормальных сечений 1 и 2.

Тогда: - это и есть уравнение Лапласа.

Капиллярное явление наблюдается в сосудах, содержащих жидкость у которых расстояние между стенками соизмеримо с радиусом кривизны пов-ти жидкости. Поведение ж-ти в капиллярных сосудах зависит от того, смачивает или нет жидкость стенки сосуда. При смачивании наблюдается поднятие уровня в капилляре за счет растяжения ж-ти, а при не смачивании наоборот- опускание в рез-те сжатия. При равновесии Лапласовское давление = гидростатическому

Где ρ - плотность жидкости, ρ₀ - плотность газовой фазы, g- ускорение свободного падения, r-радиус мениска, h - высота столба

- Уравнение Жюрена.

Где .

Следует помнить, что капиллярное явление имеет место только на границе трех фаз: твердое тело – газ – жидкость.

13. Томсона (Кельвина), зависимость давления насыщенного пара от кривизны поверхности жидкости, капиллярная конденсация.

получаем условие равновесия жидкости при наличии между ними искривлённой поверхности раздела, описываемое уравнением Томсона (Кельвина):

или приближённо , т.е. .

Из уравнения Томсона (Кельвина) видно, что равновесное давление пара для капель жидкости тем выше, чем меньше радиус капель. Уравнение Томсона (Кельвина) в приближённом виде применимо практически во всех случаях, за исключением капель размерами, приближающимися к молекулярным.

Явление капиллярной конденсации состоит в том, что конденсация пара в тонких капиллярных порах твёрдых адсорбентов происходят при давлении меньших, чем давление насыщенного пара над плоской поверхностью жидкости (при условии смачивания конденсатом поверхности адсорбента). В соответствии с законом Томсона (Кельвина) чем меньше поры адсорбента, тем при меньшем давлении происходит конденсация. Это используется в частности при рекуперации (возвращение в производство) летучих растворителей в технологических процессах, а так же для анализа геометрии порогового пространства сорбента и др.

14. Закон Гиббса-Оствальда-Фрейндлиха, влияние дисперсности на растворимость твердых частиц, процессы изотермической перегонки в дисперсных системах.

Соотношение для зависимости растворимости с(r) вещества капель и кристаллов от их размера (уравнение Гиббса – Оствальда – Фрейндлиха):

,где с0 – растворимость макроскопической фазы.

Для снижения удельной поверхности, т.е. уменьшается энергия Гиббса, процесс самопроизвольный. Перенос вещества от мелких к крупным, т.к. хим. потенциал крупных меньше (эффект Кельвина).

Обычно рассматривают три стадии процесса изотермической перегонки: растворение или испарение мелких частиц, вещества от мелких частиц к крупным и рост крупных частиц. В зависимости от условий каждая из этих стадий может быть, лимитирующей, т. е. иметь меньшую скорость и, таким образом, определять скорость всего процесса изотермической перегонки. Первую и третью стадии можно отнести к химическим, которые, как правило, имеют большие энергии активации. Очевидно, что энергии активации этих стадий при прочих иных условиях больше у твердых частиц, чем у жидких. Кинетика процессов, протекающих на поверхности частиц (растворение и рост частиц), обсуждалась при рассмотрении образования новой фазы. Вторая перенос— является диффузионной. Как известно, коэффициент диффузии сильно зависит от агрегатного состояния дисперсионной среды, в тысячи и десятки тысяч раз уменьшаясь при переходе отобранной к жидкой и от жидкой к твердой средам. Скорость изотермической перегонки часто лимитируется скоростью диффузионного массопереноса в дисперсионной среде, которая следует закону Фика и зависит в данной среде янный коэффициент диффузии только от градиентаций или давлений (разности химических потенциалов). Вочередь градиент концентраций (давлений) определяется отличием размеров частиц, между которыми происходит перенос.