5. Первый и второй законы Фика, диффузия, движущая сила диффузии, связь коэффициента диффузии с размерами частиц

Диффузией называют самопроизвольно протекающий в системе процесс выравнивания концентрации молекул, ионов или коллоидных частиц под влиянием их теплового хаотического движения; макроскопическое проявление теплового движения молекул, всегда идет тем быстрее, чем выше температура. Явление диффузии необратимо. Колличественный процесс диффузии описывается законом Фика: скорость процесса диффузии в ДС прямо пропорциональна площади, через которую осуществляется диффузия и градиенту концентрации диффундиующего вещества первый закон Фика :

m – количество продиффундировавшего вещества D – коэффициент диффузии, зависящий от свойств диффундирующих частиц и среды dc/dx – градиент концентрации –движущая сила диффузии S – площадь, через которую идет диффузия dT – продолжительность диффузии Второй закон Фика связывает пространственное и временное изменения концентрации:

Коэффициент диффузии(D) – масса вещества диффундирующего через ед. площади(1м²) за ед. времени (1с) при ед. градиенте концентрации. Энштейн установил связь КД с параметрами Д системы: D = (RT)/(6П r _ДФ η _ДСNA)

ПРИМЕРЫ:Распространение запахов, смешивание разнородных жидкостей, растворение твердых тел в жидкостях, сварка металлов при их расплавлении или под давлением.

5. закона Фика в форме принимают в качестве кинематической характеристики скорость фильтрации.

6.Проникновение растворённого вещества в клетку может быть выражено законом Фика, в котором значение коэффициента Диффузии заменено коэффициентом проницаемости мембраны, а градиент концентрации — разностью концентраций вещества по обе стороны мембраны.

7, Диффузионное проникновение в клетку газов и воды (Осмос) также описывается законом Фика; при этом значения разности концентраций заменяются значениями разности давлений газов и осмотических давлений внутри и вне клетки.

Примеры:Д. кислорода из лёгких в кровь и из крови в ткани, всасывание продуктов пищеварения из кишечника, поглощение элементов минерального питания клетками корневых волосков, Д. ионов при генерировании биоэлектрических импульсов нервными и мышечными клетками).

8, Различная скорость Д. ионов через клеточные мембраны — один из физических факторов, влияющих на избирательное накопление элементов в клетках организма.

6. Гипсометрический закон Лапласа, диффузионно-седиментационное равновесие. Кривая седиментации для монодисперсных и полидисперсных систем.

Суспензия (ж,т) была получена равномерным перемешиванием вещества в ТВ.ф. в Vд.с.(жидкой) в результате чего вещества д.ф.равномерно распределились с начальной концентрацией Седиментационная скорость направлена вниз.

После прекращения перемешивания в системе начинается процесс седиментации, который нарушает начальное распределение частиц д.ф. по Vд.с. В результате возникает градиент концентраций частиц д.ф. в верхней и нижней областях цилиндра. По мере развития процесса седиментации градиент будет расти.

Из-за возникшего градиента концентрации начинает развиваться процесс диффузии причём диффузионный поток направлен от большей частичной концентрации(низ) к меньшей частичной концентрации(верх)скорость диффузии направлена вверх.

При выравнивании скоростей седиментации и диффузии в д.сист. устанавливается седиментационно-диффузионное равновесие, при котором частицы д.ф.не равномерно распределены по высоте сосуда. Если на д.сист. находящуюся в состоянии этого равновесия не оказывать воздействия, частицы д.ф. останутся на своём месте без оседания сколь угодно долго!

Количественной оценкой с-д равновесия ф-ла Лапласа, которая имеет вид

Которая показывает на какой высоте в данной д.сист. устанавливается равновесие для частиц радиусом r.

- концентрация частиц в единице объёма на высоте h от дна сосуда.

Анализ формулы позволяет сделать вывод:

1. Между высотой и частичной концентрацией на данной высоте, существует обратно пропорциональная зависимость.

Эмульсии (жидкая – д.ф. и жидкая д.ср.)

В эмульсиях соотношение между h и обратное по отношению к суспензиям из-за отрицательного знака в скобке .

2. Связь между высотой и размером частиц обратно пропорциональна.

Гипсометрическая формула Лапласа широко используется для экспериментального установления распределения частичной концентрации как функции от высоты.

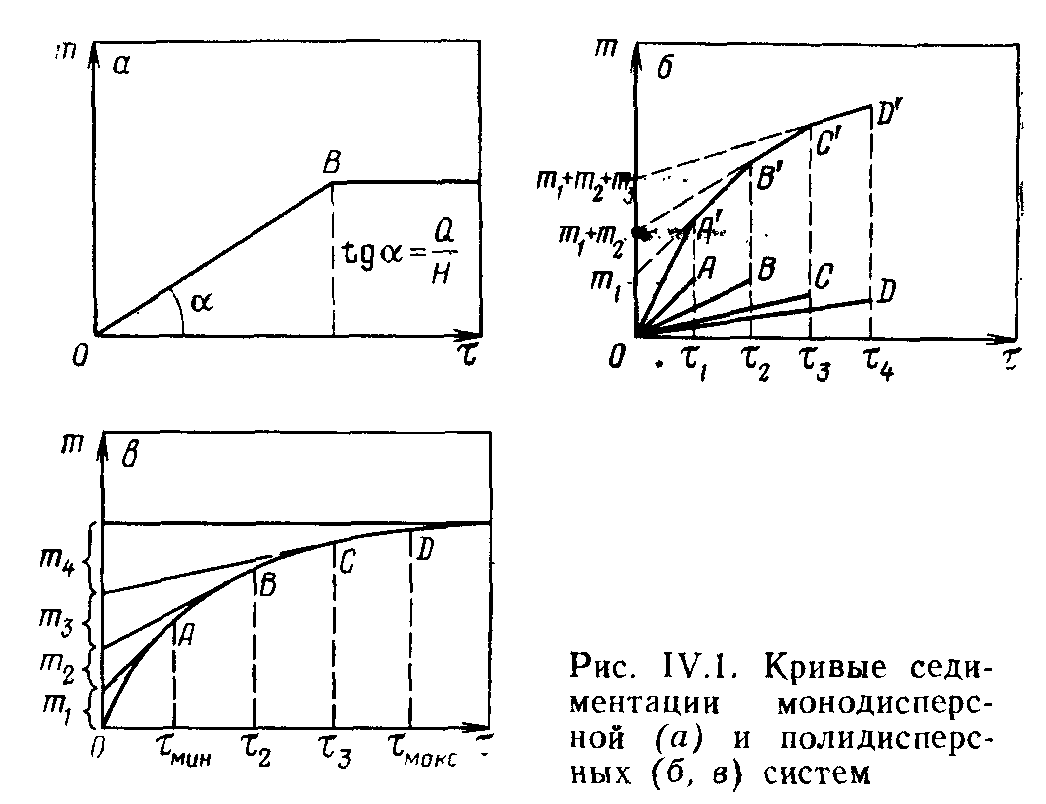
Процесс седиментации монодисперсной системы графически выражается прямой (см. рис. IV.1). Для полидисперсной системы осаждение каждой фракции описывается отдельными прямыми, представленными на рисунке IV.1б: ОА, ОВ, ОС и OD. Чем меньше размер частицы, тем меньше наклон прямой