МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ

ДОНЕЦКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Горно-геологический факультет

Кафедра технологии и техники

геологоразведочных работ

КУРСОВАЯ РАБОТА

по дисциплине

«Математическое программирование в геологоразведочной отрасли»

на тему

«Решение задачи линейного программирования применительно к геологоразведочной отрасли»

КР00.02.011.78.00

Исполнитель

студент группы ТТР-10 Сафронова А.Р.

Руководитель Филимоненко Н.Т.

Консультант Филимоненко Н.Т.

Донецк 2012

СОДЕРЖАНИЕ

Введение…………………………………………………………………..5

1. Составление математической модели………………………………..6

1.1. Выбор элементов решения……………………………………...…..6

1.2. Запись ограничений………………………………………………...6

1.3. Запись целевой функции…………………………………………...6

1.4. Приведение системы ограничений к каноническому виду………7

2. Решение задачи линейного программирования симплекс-методом………………………………………………….…………..…….9

Заключение………………………………………………………….…...19

Перечень рекомендуемой литературы…………………………………20

ЗАДАНИЕ №11

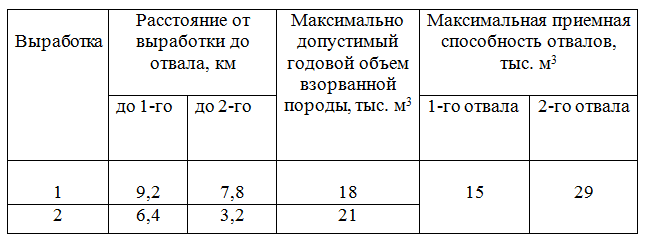
При проведении подземных горно-разведочных работ взорвана порода, которая вывозится на отвалы транспортом геологоразведочной организации. Количество отвалов, их максимальная способность, число выработок и среднее расстояние транспортировки породы от выработок на отвалы, а также допустимый годовой объем взорванной породы по каждой из выработок приведены в таблице. Составить план грузоперевозок, которые обеспечивают вывоз взорванной породы с минимальными транспортными затратами, с учетом максимальной приемной способностью отвалов.

РЕФЕРАТ

Пояснительная записка содержит: 20 с.,15 табл.,4 источника.

Объектом курсовой работы является математическая модель, которая позволяет оптимизировать в рамках заданных ограничений вывоз взорванной породы, с учетом максимальной приемной возможностью отвалов.

Цель работы - вывоз взорванной породы с минимальными транспортными затратами при соблюдении заданных ограничений с учетом максимальной приемной возможностью отвалов.

Выбрано управление. Формализовано четыре варианта ограничений и целевая функция, которая содержит четыре модели оптимизационной задачи линейного программирования. На основании расчетов с помощью компьютерной программы, которая реализует симплекс-метод, а также экспертной оценки вариантов решений определены оптимальные работы вывоза взорванной породы с минимальными транспортными затратами, с учетом максимальной приемной возможностью отвалов.

МАТЕМАТИЧЕСКОЕ ПРОГРАММИРОВАНИЕ, РЕШЕНИЕ, ОГРАНИЧЕНИЯ, ЦЕЛЕВАЯ ФУНКЦИЯ, ВЫРАБОТКА, ПОРОДА, ОТВАЛ, МИНИМАЛЬНЫЕ ЗАТРАТЫ.

ВВЕДЕНИЕ

Современная горно-разведочная организация, которая выполняет работы разного целевого предназначения, - это сложное, комплексное предприятие, и требует от руководства любого ранга умение быстро и правильно принять решения. При этом его функции все больше усложняются при необходимости работ в сложных геолого-технических условиях, а также дальнейшего развития техники и повышения требований сохранения окружающей среды.

В этих условиях решение, принятые без предыдущих расчетов, которые базируются только на инженерной интуиции и личном опыте, чаще становятся малоэффективными.

При принятии решений использовался метод математического программирования, реализация которого без ЭВМ практически невозможна.

Задание курсовой работы есть конкретная производственная задача оптимизационного характера, которая предусматривает минимальные транспортные затраты при соблюдении заданных ограничений с учетом максимальной приемной возможностью отвалов. Актуальность данной заданной задачи обусловлена тем, что основным предметом денежного расчета за выполненные работы является выполненный объем работ в тоннах на километры. Поэтому он и минимизируется.

При решении задачи использовался один из методов математического программирования - линейное программирование.

1. Составление математической модели

1.1 Выбор элементов решения

Основные понятия. Решение – всякий определенный выбор зависящих от нас параметров. Элементы решения – параметры совокупность, которых образуют решение. [3]

Элементами решения применительно к поставленной задачи будут:

х₁, х₂- оптимальные объемы породы, которые вывозятся с первой выработки, соответственно на первый и второй отвал, тыс. м³ км.

х₃, х₄- оптимальные объемы породы, которые вывозятся со второй выработки, соответственно на первый и второй отвал, тыс. м³ км.

Совокупность вышеприведенных элементов решения составляют решение задачи.

1.2 Запись ограничений

Ограничение – заданное дисциплинирующее условие операции. Ограничения бывают двух видов: физические и критериальные. Физические ограничения – это те ограничения, которые не должны быть нарушены. Критериальные – это те ограничения, которые мы можем нарушить не в ущерб достоверности математической модели. [3]

Ограничения в данном количестве объема породы.

Ограничения по максимально допустимому годовому объему взорванной породы (1.1):

(1.1)

Ограничения по максимальной приемной способности отвалов (1.2):

(1.2)

Поскольку в данной задаче способность отвалов имеет ограниченный прием породы, то эти ограничения нарушать нельзя. Поэтому это физические ограничения.

1.3 Запись целевой функции

Целевая функция – это показатель эффективности решения. [3]

В данной задаче целевая функция минимизирует транспортную работу при организации вывоза породы с горных выработок (1.3):

(1.3)

1.4 Приведение системы ограничений к каноническому виду

Система ограничений, которая представляет математическую модель, имеет вид (1.4):

(1.4)

Данную математическую модель, а именно систему ограничений неравенств необходимо привести к каноническому виду, позволяющему записать ее в симплекс-таблицу. Для этого систему ограничений неравенств приводят к эквивалентной системе уравнений (1.5) путем введения в каждое неравенство вспомогательной, неотрицательной переменной у со знаком «+» или «-» в зависимости от знака отношения. [1]

(1.5)

Канонический вид системы уравнений будет выглядеть следующим образом (1.6):

(1.6)

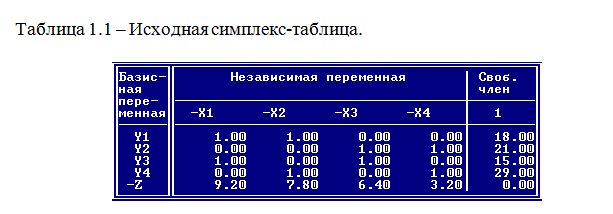
После приведения системы уравнений к каноническому виду, данные системы ограничений заносим в симплекс-таблицу (табл. 1.1). При занесении системы ограничений в симплекс-таблицу, необходимо изменить знак на противоположный у элементов независимых переменных. Так как в базисном решении все независимые переменные равны нулю (х = 0). [1]

Таким образом, математическая модель, записанная в симплекс-таблице, будет иметь вид: