4. Виды моделирования. Различные модели исследования операций

Моделирование широко распространено, поэтому достаточно полная классификация возможных видов моделирования крайне затруднительна хотя бы в силу многозначности понятия «модель».

Виды моделирования:

• концептуальное моделирование, при котором с помощью некоторых специальных знаков, символов, операций над ними или с помощью естественного или искусственного языков истолковывается основная мысль относительно исследуемого объекта;

• интуитивное моделирование, которое сводится к мысленному эксперименту на основе практического опыта работников;

• физическое моделирование, при котором модель и моделируемый объект представляют собой реальные объекты или процессы единой или различной физической природы;

• структурно-функциональное моделирование, при котором моделями являются схемы, графики, чертежи, диаграммы, таблицы, рисунки, дополненные специальными правилами их объединения и преобразования:

• математическое моделирование, при котором моделирование, включая построение модели, осуществляется средствами математики и логики;

• имитационное моделирование – это метод, позволяющий строить модели, описывающие процессы так, как они проходили бы в действительности. Такую модель можно испытать во времени как для одного случая, так и для множества. Результаты будут определяться случайным характером процессов, т.е. ИМ – это метод исследования, при котором изучаемая система заменяется моделью, хорошо описывающей реальность. С этой моделью проводятся эксперименты (имитации) с целью получения информации по системе.

К ИМ прибегают, когда:

-дорого или невозможно экспериментировать на реальном объекте,

-невозможно построить аналитическую модель,

-необходимо сымитировать поведение системы во времени.

Перечисленные выше виды моделирования не являются взаимоисключающими и могут применяться при исследовании сложных объектов либо одновременно, либо в некоторой комбинации.

Компьютерное моделирование является развитием имитационного моделирования, а также математического моделирования.

Компьютерное моделирование – это метод решения задачи анализа или синтеза объекта на основе использования его компьютерной модели.

Мат. Моделирование-процесс построения и изучения мат. модели.

Сущность методологии мат моделирования состоит в замене объекта математической моделью и дальнейшее изучение этой модели с помощью реализуемых на компе вычислительных алгоритмов.

Модель

Объект

Алгоритмы

Программа

5. Основная задача линейного программирования.

Математическое программирование – это один из разделов исследования операций – прикладного направления кибернетики.

Цель-разработка аналитических методов определения решения.

Задачи МП имеют большое число переменных и ограничений. Объем вычислительных работ очень велик, процесс нахождения решения невозможен без применения компьютера и компьютерных технологий.

Целевая функция в экстремальных задачах (задач на экстремум) – функция, минимум или максимум которой необходимо найти. Найдя экстремум целевой функции, и определив значения управляемых переменных, которые к нему приводят, мы тем самым находим оптимальное решение задачи.

Целевая ф-я выступает как критерий оптимальности решения задачи.

Среди задач МП самыми простыми являются задачи так называемого линейного программирования (ЛП). Для этих задач характерно:

• Целевая функция (показатель эффективности) линейно зависит от элементов х1,х2,…хn.

• Ограничения, налагаемые на элементы решения, имеют вид линейных равенств или неравенств относительно х1,х2,…хn.

Любую задачу ЛП можно свести к стандартной форме так называемой основной задаче линейного программирования (ОЗЛП), которая формулируется следующим образом: найти такие значения переменных х1,…,хn, которые удовлетворяли бы условиям-равенствам и условию не отрицательности, а также обращали бы в макс линейную ф-ю этих переменных.

6.Задача о пищевом рационе.

Ферма производит откорм скота с коммерческой целью.

Допустим, что имеется всего четыре вида продуктов: П1, П2, П3 и П4. Стоимость единицы каждого продукта с1, с2, с3 и с4. Из этих продуктов требуется составить пищевой рацион, который должен содержать: белков – не менее в1 единиц, углеводов – не менее в2 единиц, жиров – не менее в3 единиц. Для продуктов П1, П2, П3 и П4 содержание белков, углеводов и жиров (в единицах на единицу продукта) известно и задано в таблице, а i j – определенные числа, первый индекс указывает на номер продукта, а второй – на номер элемента (белки, углеводы, жиры).

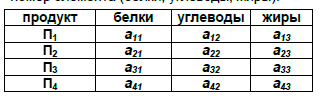
Требуется: составить такой пищевой рацион (то есть указать количества продуктов П1, П2, П3и П4, входящих в него), чтобы условия по белкам, углеводам и жирам были выполнены и при этом стоимость рациона была минимальна.

Составим математическую модель.

Обозначим через x1 , x2 , x3 , x4 - количества продуктов П1, П2, П3 и П4, входящих в рацион.

Показатель эффективности, который требуется минимизировать, – стоимость рациона L;

стоимость линейно зависит от элементов решения х1,х2,х3,х4, то есть L=c1x1+c2x2+c3x3+c4x4

Запишем в виде формул ограничительные условия по белкам, углеводам и жирам. Учитывая, что в одной единице продукта П1 содержится а11 единиц белка, а в х1 единицах - а11 х1 единиц белка, в х2 единицах продукта П2 содержится а21 х2 единиц белка и так

далее, получим три неравенства:

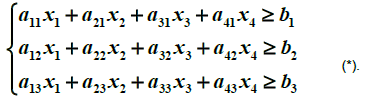
Эти линейные неравенства представляют собой ограничения, накладываемые на элементы решения х1,х2,х3,х4.

Таким образом, поставленная задача сводится к следующей: найти такие

неотрицательные значения переменных х1,х2,х3,х4 , чтобы они удовлетворяли ограничениям-неравенствам (*) и одновременно обращали в минимум линейную функцию этих переменных