40. Сэр с запоминанием экстремума.
Входная величина изменяется с постоянной скоростью U. Значение U поступает на устройство запоминания экстремума, которое работает след. образом:
Пока У увеличивается У* следит за ним, т.е. У=У* .
Как только У начинает уменьшаться У* перестает изменяться и У*=const и происходит запоминание экстремального значения.
Специальный блок определяет разность текущего У и У*. Как только разность достигает критического значения происходит реверс входа и стирается запомненное оптимальное значение и У*=У
Простейшее устройство запоминания – это с использованием диода и конденсатора:
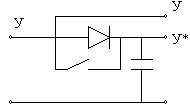
Достоинства:
Можно применять на объектах, имеющих узкую полосу частот
Не надо диф-ть сигнал
Недостаток:
Трудность выбора У
41. Сэр шагового типа.
В этой системе управление изменяется шагами. После каждого шага анализируется результат предыдущего шага и если новое значение У лучше предыдущего, то делается шаг в этом же направлении, если хуже, то в противоположном.
Величина шага м.б. переменной или постоянной. Данная система удобна для объектов с транспортным запаздыванием.
К1 и К2 работают синхронно через промежуток t.
УЗ – устройство задержки на 1 такт
Sign – знаковое реле. Срабатывает только в случае, когда разница (Уn-Уn-1) меняет знак.
1. Постановка задачи оптимального управления. Критерии оптимальности.
2. Экономическая оценка эффективности процессов.
3. Постановка задачи оптимального управления в статике.
4. Постановка задачи оптимального управления в динамике.
5.Исследование одномерной целевой функции на экстремум методом классического анализа.
6. Одномерный поиск экстремума целевой функции методом сканирования.
7.Одномерный поиск экстремума целевой функции методом золотого сечения.
8.Одномерный поиск экстремума целевой функции методом с использованием чисел Фибоначчи.
9. Исследование многомерной целевой функции на экстремум методом
классического анализа.
10.Решение многомерной задачи оптимизации на условный экстремум.
Метод неопределенных множителей Лагранжа.
11.Поиск экстремума функции многих переменных методом сканирования
12.Метод многомерного поиска экстремума. Метод релаксаций и метод Гаусса-Зайделя.
13.Метод градиента. Метод наискорейшего спуска.
14.Поиск экстремума целевой функции при наличии оврагов.
15.Решение задач нелинейного программирования при ограничениях типа равенства.
16.Решение задач нелинейного программирования при ограничениях типа неравенства.
17.Методы случайного поиска.
18.Линейное программирование. Примеры постановок задач линейного программирования.
19.Свойства оптимальных решений в задачах линейного программирования.
20.Симплекс-метод.
21.Динамическое программирование. Принц оптимальности и принцип вложения.
22.Решение задач оптимизации методом динамического программирования. Уравнения Беллмана.
23. Последовательность принятия решений в динамическом
программировании. Функциональные уравнения.
24.Вариационное исчисление. Классы допустимых функций.
25.Уравнение Эйлера для простейшего функционала. Условие Лежандра. Пример решения уравнения Эйлера.
26.Уравнение Эйлера и условие Лежандра для функционала, зависящего от N-функций и их первых производных.
27. Уравнение Эйлера и условие Лежандра для функционала, зависящего от
функции и от N её производных. Пример.
28.Уравнение Эйлера для функционала, зависящего от N-функций и от N-производных. Пример.
29.Решение экстремальной задачи с подвижными границами. Условие трансверсальности. Пример.
30.Решение вариационных задач на условный экстремум при наличии интегральной связи. Пример.
31. Решение вариационных задач на условный экстремум с голономными
связями.
32.Решение вариационных задач на условный экстремум с неголономными
связями.
33. Особенности решений вариационных задач оптимального управления.
34. Принцип максимума Понтрягина. Роль советских ученых в разработке ПМ.
35. Последовательность решения задач с помощью ПМ.
36. Задача синтеза системы оптимального управления. Её решение с помощью принципа максимума. Пример.
37.Понятие о СЭР. Необходимые условия применения экстремальных регуляторов.
38.Система экстремального регулирования (СЭР) с измерением производной.
39. СЭР со вспомогательной модуляцией.
40. СЭР с запоминанием экстремума.
41.Система экстремального регулирования шагового типа.