Основные свойства системы Навье — Стокса

-При превышении числа Рейнольдса выше некоторого критического числа, аналитическое точное решение для пространственного или плоского потока имеют хаотический вид (так называемая турбулентность). В частном случае, оно связано с теорией Фейгенбаума или другими сценариями перехода к хаосу. При уменьшении числа Рейнольдса ниже критического, решение опять принимает не хаотический вид.

-Исключительная чувствительность к изменению коэффициентов уравнения при турбулентном режиме: при изменении числа Re на 0,05 % решения совершенно отличаются друг от друга.

-Существует мнение, что данное уравнение является приближенным. Это обосновывается использованием при выводе уравнения Навье-Стокса линейного уравнения для нахождения давления p, как функции его нелинейных компонентов. Такая позиция объясняет существование различных значений числа Рейнольдса (для различных частных задач), в пределах которого линейный закон осреднения корректен.

Применение

Будучи дополненным уравнениями переноса тепла и переноса массы, а также соответствующих массовых сил, система уравнений Навье — Стокса может описывать конвекцию, термодиффузию в жидкостях, поведение многокомпонентных смесей различных жидкостей и т. п.

Если же в уравнение в качестве массовой силы ввести силу Лоренца, и дополнить систему уравнениями Максвелла для поля в сплошной среде, то модель позволяет описывать явления электро- и магнитогидродинамики. В частности, такие модели успешно применяются при моделировании поведения плазмы, межзвёздного газа.

Одним из применений системы уравнений Навье — Стокса является описание течений в мантии Земли («проблема динамо»).

Также вариации уравнения Навье — Стокса используются для описания движения воздушных масс атмосферы, в частности, при формировании прогноза погоды. Для описания реальных течений в различных технических устройствах приемлемую точность численного решения можно получить только при такой расчётной сетке, ячейки которой меньше самого мелкого вихря. Это требует очень больших затрат расчётного времени на современных компьютерах. Поэтому были созданы различные модели турбулентности, упрощающие расчёт реальных потоков.

Уравнение Эйлера — одно из основных уравнений гидродинамики идеальной жидкости. Названо в честь Л.Эйлера, получившего это уравнение в 1755 году. По своей сути является уравнением движения жидкости.

Классическое уравнение Эйлера

Рассмотрим движение идеальной жидкости. Выделим внутри неё некоторый объём V. Согласно второму закону Ньютона, ускорение центра масс этого объёма пропорционально полной силе, действующей на него. В случае идеальной жидкости эта сила сводится к давлению окружающей объём жидкости и, возможно, воздействию внешних силовых полей. Предположим, что это поле представляет собой силы инерции или гравитации, так что эта сила пропорциональна напряжённости поля и массе элемента объёма. Тогда

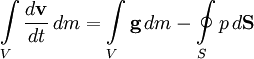
где S — поверхность выделенного объёма, g — напряжённость поля. Переходя, согласно формуле Гаусса — Остроградского, от поверхностного интеграла к объёмному и учитывая, что , где ρ — плотность жидкости в данной точке, получим:

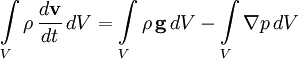
В силу произвольности объёма V подынтегральные функции должны быть равны в любой точке:

Выражая конвективную производную через частные производные:

получаем уравнение Эйлера для движения идеальной жидкости в поле тяжести:

где — плотность жидкости,

— давление в жидкости,

— вектор скорости жидкости,

— вектор напряжённости силового поля,

• — оператор набла для трёхмерного пространства.

Частные случаи

Стационарный одномерный поток

Для случая стационарного, одномерного потока жидкости или газа уравнение Эйлера принимает вид:

В этой форме уравнение часто используется для решения различных прикладных задач гидродинамики и газодинамики. В частности, интегрированием этого уравнения по x при постоянной плотности жидкости ρ получается известное уравнение Бернулли для несжимаемой жидкости:

Несжимаемая жидкость

Пусть ρ = const. Используя известную формулу,

перепишем соотношение в форме

Беря ротор и учитывая, что,

а частные производные коммутируют, получаем что

Адиабатическое течение

В случае, если происходит адиабатическое движение жидкости, то уравнение Эйлера можно переписать с использованием тепловой функции следующим образом:

в силу того, что при адиабатическом процессе энтропия s постоянна.

Следовательно:

7. Гидравлический удар (гидроудар) — скачок давления в какой-либо системе, заполненной жидкостью, вызванный крайне быстрым изменением скорости потока этой жидкости за очень малый промежуток времени. Гидравлический удар способен вызывать образование продольных трещин в трубах, что может привести к их расколу, или повреждать другие элементы трубопровода.

Общие сведения

Явление гидравлического удара открыл в 1869 г. Н. Е. Жуковский. Увеличение давления при гидравлическом ударе определяется в соответствии с его теорией по формуле:

,

где Dp — увеличение давления в Н/м²,

ρ — плотность жидкости в кг/м³,

v0 и v1 — средние скорости в трубопроводе до и после закрытия задвижки (срабатывания клапана) в м/с,

с — скорость распространения ударной волны вдоль трубопровода.

Жуковский доказал, что скорость распространения ударной волны c находится в прямо пропорциональной зависимости от сжимаемости жидкости, величины деформации стенок трубопровода, определяемой модулем упругости материала E, из которого он выполнен, а также от диаметра трубопровода.

Следовательно, гидравлический удар не может возникнуть в трубопроводе, содержащем газ, так как газ легко сжимаем.

Зависимость между скоростью ударной волны c, её длиной и временем распространения (L и τ соответственно) выражается следующей формулой: