34. Дифференциальные уравнения поступательного движения твердого тела.

При поступательном движении все точки тела движутся так же, как и центр масс, значит:

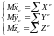
Задачи:

1. по закону движения определить главный вектор внешних сил, действующих на точки данного тела. При этом главный вектор момент всех внешних сил относительно центра масс равен нулю.

2. по внешним силам и начальным условиям найти закон движения тела.

Дифференциальные уравнения вращательного движения твердого тела.

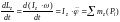. Аналогично для двух других осей:

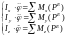
Задачи:

1. по закону движения и моменту инерции определить главный вектор момент всех внешних сил, действующих на точки данного тела.

2. по внешним силам, моментам инерции и начальным условиям найти закон движения тела.

3. по внешним силам и угловому ускорению определить момент инерции.

Дифференциальные уравнения плоскопараллельного движения твердого тела.

Плоскопараллельное движение состоит из поступательного вместе с центром масс и вращательного вокруг него:

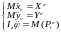
36. Явление удара.

Явление, при котором, за ничтожно малые промежутки времени скорости точек тела изменяются на конечную величину, называется ударом.

Силы, которые изменяют скорости точек в течении малого промежутка времени называются мгновенными или ударными.

Фаза изменения скоростей – фаза деформации

τ₁ – время фазы деформации Sд=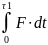

τ₂ – время фазы восстановления Sв=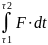

Коэффициент восстановления при ударе K=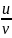

u – скорость после удара v – скорость до удара

Если К=0, то u=0 – абсолютно неупругий удар

Если К=1, то u=v – абсолютно упругий удар

Если 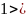К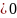 – упругий удар

37. Теоремы теории удара

-Теорема об изменении количества движения при ударе (Изменение количества движения системы за время удара, равно сумме всех внешних ударных импульсов действующих на систему: Q-Q_i=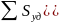

-Теорема об изменении кинетического момента при ударе (Изменение за время удара кинетического момента системы относительно центра, ровно сумме моментов всех действующих на систему ударных импульсов: L-L₀=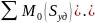

-Теорема об изменении кинетической энергии при ударе (Т. Карно) (Кинетическая энергия потерянная системой, при абсолютно неупругом ударе, равна той кинетической энергии, которую имела бы система, если бы ее тела двигались с потерянными скоростями:

T-T₀=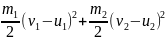 ).