29. Принцип Даламбера для материальной точки.

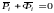
Геометрическая сумма всех приложенных к движущейся материальной точке сил и сил инерции этой точки равна нулю

Принцип Даламбера для несвободной механической системы.

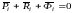
В движущейся несвободной механической системе для каждой материальной точки в любой момент времени геометрическая сумма приложенных к ней задаваемых сил, реакций связи и сил инерции равна нулю. Умножив обе части выражения на r_i получим: ; .

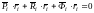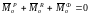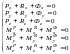, сумма моментов задаваемых сил, реакций связи и сил инерции относительно осей координат равна нулю.

30. Приведение сил инерции точек твердого тела к простейшему виду.

К системе сил инерции точек твердого тела, можно применить метод Пуансона, рассмотренный в статике. Тогда любую систему сил инерции можно привести к главному вектору сил инерции и главному моменту сил инерции.

-при поступательном движении: Ф=-ma (при поступательном движении твердого тела, силы инерции его точек приводятся к главному вектору сил инерции равному по модулю произведению массы тела, на ускорение центра масс приложенному в этом центре и направленному в сторону противоположному ускорению центра масс).

-при вращательном движении: М=-Iε (при вращательном движении твердого тела силы инерции его точек приводятся к главному моменту сил инерции равному произведению момента инерции тела относительно сил вращения на угловое ускорение. Направлен этот момент в сторону противоположному угловому ускорению).

-при плоском движении: Ф=-ma М=-Iε (при плоском движении твердого тела силы инерции его точек приводятся к главному вектору и главному моменту сил инерции).

31. Общее уравнение динамики. Принцип Даламбера-Лагранжа.

Принцип Даламбера: (P_i + R_i + Ф_i) = 0; (P_i + R_i + Ф_i)r_i = 0, полагаем. что связи, наложенные на механическую систему двусторонние, стационарные, голономные и идеальные, тогда: (R_i  r_i) = 0;

(P_i + Ф_i)r_i = 0 - общее уравнение динамики - для движения механической системы с двусторонними, стационарными, голономными и идеальными связями сумма работ задаваемых сил и сил инерции точек системы на любом возможном перемещении равна нулю.

32. Обобщенные координаты, обобщенные силы и их вычисление.

Обобщенная координата q_i - независимая величина, заданием которой однозначно определяется положение всех точек механической системы.

Обобщенная сила - Q_i - соответствующая обобщенной координате q_i - скалярная величина, равная отношению элементарной работы сил, действующих на систему на перемещении, вызванном элементарным приращением обобщенной координаты к величине этого приращения: .

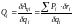33. Уравнение Лагранжа второго рода.

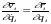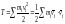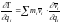Пускай q - обобщенная координата, зависящая от времени. Производная по времени от обобщенной координаты - обобщенная скорость, тогда: . Кинетическая энергия механической системы: . Частная производная кинетической энергии по обобщенной координате: , частная производная кинетической энергии по обобщенной скорости: 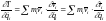. Продифференцируем последнее выражение по времени: 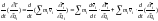; учитывая, что: 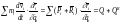и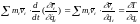 получим: 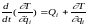или .
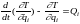