14. Главные оси и главные моменты инерции.

Главная ось инерции - ось, относительно которой центробежный момент равен нулю. Если для тела существует материальная ось симметрии, то главная ось инерции совпадает с ней. Если все центробежные моменты инерции равны нулю, то каждая из осей является главной осью инерции.

Главная центральная ось инерции - центральная ось инерции, проходящая через центр масс.

Главные моменты инерции - моменты инерции относительно главных осей

15. Теорема о моменте инерции относительно параллельных осей.

Теорема: Момент инерции относительно оси равен сумме момента инерции относительно параллельной ей центральной оси и произведение массы тела на квадрат расстояния меду осями: I_z = I_zc + mh².

16. Моменты инерции простейших тел.

Для однородного стержня: I_zc = ml²/12;

для однородного кольца (тонкостенный цилиндр): I_zc = mR²;

для однородного диска (однородный цилиндр): I_zc = mR²/2;

для полого однородного цилиндра: I_zc = m(R₁²-R₂²)/2;

для однородного шара: I_zc = 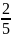mR²;

для однородного кругового конуса: I_zc = 0,3mR²;

17. Радиус инерции.

Радиус инерции - расстояние от оси до воображаемой точки, в которой необходимо сосредоточить массу тела, чтоб момент инерции этой точки относительно заданной оси был равен моменту инерции данного тела относительно этой же оси: 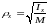Центробежный момент инерции: .

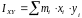18. Теорема об изменении количества движения материальной точки.

Количество движения материальной точки - вектор, численно равный произведению массы точки на скорость ее движения и совпадающий с ней по направлению.

Векторная производная по времени от количества движения материальной точки геометрически равна вектору силы, действующей на точку.

Основное уравнение динамики: 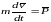; 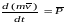. Интегрируя получим: ; .

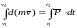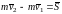Теорема: Изменение количества движения материальной точки за некоторый промежуток времени равно импульсу силы, действующей на точку за этот промежуток времени.

Теорема об изменении количества движения механической системы.

Количество движения механической системы - вектор, равный геометрической сумме всех количеств движения материальных точек этой системы, численно равный произведению массы системы на скорость центра масс и совпадающий с ней по направлению.

Векторная производная по времени от количества движения механической системы геометрически равна главному вектору внешних сил, действующих на механическую систему.

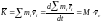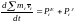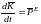. Так как: , то: ; интегрируя получим: ; .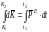

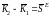Теорема: Изменение количества движения механической системы за некоторый промежуток времени равно геометрической сумме импульсов внешних сил, действующих на систему за этот промежуток времени.

Следствия:

1. внутренние силы не влияют на изменение количества движения;

2. Закон сохранения количества движения механической системы: если главные векторы всех внешних сил, действующих на точки системы, равны нулю, то вектор количества движения механической системы остается постоянным.

3. Закон сохранения проекции вектора количества движения механической системы: если проекции векторов всех внешних сил, действующих на точки системы, на ось равны нулю, то проекция вектора количества движения механической системы на эту ось остается постоянной.