Постоянный ток 1. ток. Напряжение. Мощность. Ток- упорядоченное движение заряженных частиц под действием заряженного поля. Подразделяется: постоянный, переменный, импульсный. Размерность А-амперы. Количество определяется зарядом прошедшим ед. времени. , где Q-заряд, размерность кулон, Кл. t-время, размерность в сек. Напряжение- энергия затрачиваемая по перемещению ед.заряда. U=W/Q , где W- энергия, Дж. Мощность – имеем W=UQ. Исп. Q=It, получаем W=UIt. Мощность – энергия затрачиваемая в единицу времени. Обозначается P=W/t=UI, размерность ват Вт.

Элементы электрической цепи. Электрической цепью наз.совокупность различных электрических устройств соединенных определенным способом с помощью проводников. В любую электрическую цепь могут входить пассивные и активные элементы к пассивным относят сопротивление, индуктивность, конденсатор. К активным: полупроводниковые приборы, двигатели и т.д.

Сопротивление-элемент электрической цепи облодающий свойством преобразовывать электрическую энергию в тепло. Обозначение R. Различают линейное сопротивление, в котором связь между током и напряжением определяется законом Ома U=IR. Размерность в Ом. Индуктивность- элемент электрической цепи облодающий свойством накапливать энергию магнитного поля. Обозначается L. Связь между током и напряжением определяется только на переменном токе Размерность, Гн. Конденсатор- элемент электрической цепи способный накапливать энергию электрического поля. Обозначается С. Q=CU. Размерность в фарадах Ф.

Состав электрической цепи. Любая электрическая цепь содержит ветви, узел, контур. Узел-место соединения двух и более проводников (ветвей). Ветвь- участок электрической цепи между узлами содержащие один и более элементов электрической цепи. Контур- замкнутое соединение нескольких ветвей.

Источники напряжения и тока относятся к независимым активным элементам. Источники напряжения. Идеальный источник напряжения имеет вольт- амперную характеристику у которого напряжение на зажимах не зависит от отбираемого тока. Идеальные источник напряжения имеет внутреннее сопротивление R=0. Обозначается на схемах E. Вольт-амперная характеристика реального источника напряжения, который обладает определенным внутренним сопротивлением. Снижение напряжения U на зажимах обусловленнопадение напряжения на внутреннем сопротивлении. Источник тока. Идеальный источник тока характеризуется вольт- амперной характеристикой у которого ток отдаваемый в электрическую цепь не зависит от создаваемого напряжения на нагрузке. На схемах обозначается I. Так же обладает бесконечным внутренним сопротивлением. Реальные источники тока имеют конечное внутреннее сопротивление. Поэтому при некотором сопр. Нагрузки, нагрузка будет влиять на отдаваемый ток в нагрузку.

Закон Кирхгофа. При расчете электрической цепи используют принцип моделирования- реальная цепь заменяется моделью в которой элементы цепи в отл.от физических задаются точно. Для расчета электрической цепи используют закон Кирхгофа, принцип наложения, метод контурных токов, метод узловых потенциалов и др. при расчете по законам Кирхгофа исп. 2-а закона. 1-й закон Кирхгофа- алгебрагическая сумма токов ветвей сходится в узле и равна нулю. 2-й закон Кирхгофа алгебрагическая сумма напряжений на ветвях замкнутого контура равняется алгебрагической сумме источников питания и напряжений действующих в данном контуре.

Правило составления уравнений по законам Кирхгофа: 1) в заданной цепи определяем количество ветвей в которых неизвестны токи (ток в ветви содержащий источник тока равен току данного источника). 2) произвольно с помощью стрелок около ветвей задаются предпологаемые направления тока в данной ветви. 3) по первому закону Кирхгофа сост. (n-1) уравнений где n- число узлов в схеме. 4) остальные уравнения для расчета схемы составляются с использованием 2-го закона Кирхгофа. Общее кол-во сост.уравнений по законам должно соответствовать числу токов данной схемы. 5) если в результате расчета схемы получено отрицательное значение тока, это означает, что действительное обратно предложенному.

Метод контурных токов. Согласно методу для расчета схемы уравнение сост.только с использование 2-го закона К. Отличие вводится понятие контурый ток- ток который протекает по всем ветвям выбранного контура. В результате расчета получается значение для контурных токов. Токи в ветвях определяются по следующей схеме: а) ток в ветви по которой протекает только 1 контурный ток, равен контурнуму току. б) ветви принадлежащей нескильким смежным контурам, ток опр.суммой (разностью) соответствующих контурных токов. Пример: провести анализ схемы с использованием законов Кирхгофа и методов контурных токов. а) сост. Уравненийс исп.законов Кирхгофа-5 схема имеет 5 ветвей которые не имеют токи. Схема имеет 3 узла (n-1)=(3-1)=2 уравнения I1-I2-I3 (1); I2-I4-I5=0 (2). Для нахождения неизвестных токов необходимо иметь 5 уравнений. Для оставшихся 3-х уравнений исп.правило 2-го закона Кирхгофа. Для составления уравнения выбираем контуры. Каждый выбранный контур от других отличается хотябы одной выбранной ветвью. Для составления уравнения задаемся направлениями обхода контуров (выбираем по часовой стрелке). для контура 1 I1R1+I2R2=E. Для контура 2 I3R3+I4R4-I2R2=0. Для контура 3 I5(R5+R6)-I4R4=0 б) расчет схемы с использованием контурного тока. Контурный ток это ток который протекает по всем ветвям контурного тока. Пунктиром показаны контурные токи в каждом контуре. Направлены по часовой. Обозначение их I11, I22, I33.

Для контура 1 I11R1+I11R2-I22R2=E, третья составляющая уравнения учитывает, что по ветви с сопротивлением R2 протекает так же контурный ток I22. Знак – обусловлен противоположным направлением токов I11 и I22. Аналогично сост уравнения для контуров 2 и 3. Для 2 I22(R3+R2+R4)-I22R2-I33R4=0. Для 3 I33(R4+R5+R6)-I22R4. Определение токов в ветвях I1=I11; I2=I11-I22; I3=I22; I4=I22-I33; I5=I33.

Принцип наложения. Согласно принципу, ток в ветви можно определить через частичные токи, которые задаются каждым источником напряжения включенных в заданную цепь или схему. согласно методу схкма разбивается на 2-е частичные схемы содержащие источник напряжения. Из частичной схемы 1 для частичного тока . Из частичной схемы 2 для частичного тока . Отсюда .

Метод эквивалентного гениратора. Используется для расчета тока в отдельной взятой ветви

напряжение Uxx=(E₁/R₁+R₃)*R₃. Создается пассивный двухполюсник путем исключения источника E₁. Эквивалентное сопротивление данного пассивного двухполюсника является его входным сопротивлением относительно U_аб: R_э=R₁R₃/R₁+R₃. Составленная схема двухполюсника с U_хх и R_э к которым подключили ранее отброшеннуб ветвь. Согласно схеме имеем I₂=U_xx-E₂/R_э+R₂

Переменный ток. Под переменным током понимается ток, который можно представить с помощью простейших функций Sin и Cos (обозначается i) i=I_mSinα, где I_m- амплитуда максимального значения переменного тока. Переменный ток можно изобразить на плоскости с помощью радиус вектора длинной равной амплитуде I_m, которая вращается около начала координат с угловой скоростью ω. Проекция радиуса вектора в любой момент времени на ось ординат представляет собой мгновенное значение тока α=ωt- текущее значение угла. Если α=2π, то t=T- имеем 2π=ωT, т.к. T=1/f, где f- циклическая частота переодического процесса, то ω=2πf отсюда i=I_mSinωt. Промышленная частота f=50Гц.

Если радиус вектор I_m в начальный момент времени образует некоторый угол фи с осью абцисс, то выражение переменного тока имеет вид: i=I_mSin(ωt±фи).

Действующее значение переменного тока. Понимается такой постоянный ток, который на одном и том же сопротивлении за периуд выделяет столько же тепла, что и постоянный ток. Связь: I=I_m/

Пассивные элементы оси переменного тока. а) сопротивление. Имеем i=I_mSinωt, фи начальная фаза равна 0. Используем закон Ома U=iR, U=I_mRSinωt=U_mSinωt, где U_m- амплитуда напряжения. Из уравнений видно, что аргумент функции Sin не меняется. Поэтому вектора представляющие амплитуды тока и напряжения параллельны друг другу и их можно совместить с осью абцисс. б)связь между током и напряжением на индуктивности определяется выражением U_i=L*(di/dt). (1)Возьмем i=I_mSinωt (2). Используя (2) из (1) U₂=LωI_mCosωt=LI_mωSin(ωt+90). Выражение Lω=Х_L индуктивное сопротивление, выражается в Ом. (реактивное). в) конденсатор цепи переменного тока. Связь U_c и i определяется выражением i_с=c*dU_c/dt (1). Возьмем U_с=U_mcSinωt (2). Используя (2)из (1): получаем i_c=U_mcC*ωt=U_mcωC*Sin(ωt+90). Возьмем ωС=1/Х_с-реактивное емкостное сопротивление, Ом. Окончательно i_c=(U_mc/x_c)*Sin(ωt+90) (4) из (2) и (4) следует, что ток через конденсатор опережает напряжение на нем на 90 градусов.

Последовательная R-L-C цепь последовательного тока. Схема: согласно 2-у закону кирхгофа в любой момент времени сумма входного напряжения будет равна сумме напряжений на каждом элементе цепи. В векторной форме выражение имеет вид (1) сложим согласно уравнению (1) вектора на момент времени t=0. Сложение будем проводить для действующих значений. Вектор тока совмещем с осью абцисс. Под углом 90 строим U_L т.к. действующее значение тока и напряжения совподают по фазе, то вектор U_R совмещаем с током, напряжение U_L опережает ток на 90. Поэтому из конца U_L в сторону опережения под углом 90 вверх проводим вектор U_L. Вектор напряжения U_C отстает от тока на 90, поэтому из конца вектора U_L в сторону отставания проводим вектор U_C. U- представляет собой напряжение на цепи.

Треугольник АВС называется треугольником напряжения из , угол между U и I обозначим через фи, тогда фи=arctg(U_L-U_c/U_R). если U_Lбольше U_c, то фи больше 0, характер цепи будет активно индуктивный, т.к. U опережает ток. Если U_L-U_c ≤0, то фи меньше нуля ток опережает напряжение характер цепи, активно емкостной.

Треугольник с сопротивлением. имеем треугольник U делим стороны треугольника на ток I Вводим z=U/I- полное сопротивление цепи в Ом. U_x/I=x-полное реактивное сопротивление цепи, Ом. Получаем треугольник сопротивление R из треугольника R: z= , фи=arctg(x/R), U_X/I=U_L/I-U_c/I|:I, U_x=U_L-U_c, отсюда х=х_L-х_C поэтому фи=arctg (X_L-X_C/R)

Резонансное напряжение. Рассмотрим зависимость реактивных сопротивлений X_L и X_C от угловой скорости ω. Имеем X_L=ωL и X_c=(ωC)^-1 из зависимости следует что существует т.А в которой сопротивление X_L и X_C равны : ωL=1/ωC, откуда ω=1/(LC)^1/2- резонансная частота. Явление наблюдается в последовательной цепи и называется резонансом напряжения. Умножим X_L и X_C на I и получим , что U_L=U_C т.е. все приложенные напряжения к цепи выделяется на сопротивлении. При резонансе напряжений угол между током и напряжением=0. Для R-L-C цепи z=R^2. Т.к. X_L=X_c, то z= . Z=R: цепь имеет чисто активный характер. Напряжение на индуктивности и на конденсаторе каждое в отдельности может значительно превышает входное напряжение используемое в технике для повышения напряжения при нагрузке при подключении её параллельно одному из элементов L или C. Ток в последовательном контуре опр.выражением: I=U/Z. Т.к. при резонансном напряжение X_L=X_C, то I=U/R. Т.к.при резонансе напряжение уменьшается ток достигает максимального значения. Резонансная кривая тока имеет вид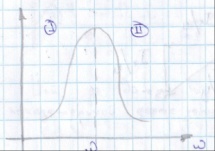 в области 1 характеристика цепи активно емкостной во 2 активно индуктивный.

Комплекс проводимости.

G= См; Y= ; z= Запишем комплексное сопротивление в тригонометрической форме =R+jx; = Определим

( ); ( При переходе от комплексного сопротивления к комплексной проводимости знак у мнимой единицы меняется на противоположный.

Комплексная мощность.

S= Вс Ток и напряжение на комплексной плоскости представляются радиус-векторами с заданной длиной равными их амплитуде с нечётными фазами. ; ; ;

Комплексная мощность определяется произведением действующих значений напряжений на комплексно сопряжённый ток.

Комплексное напряжение. Переход от комплексного напряжения к мгновенным. Комплекс действующего напряжения имеет вид : =U где – угол между током и напряжением. После умножения получаем комплекс амплитуды напряжения = Мгновенное значение напряжения зависит от времени u= Переход от комплексных к переходным значениям U= = = = Удобство использования комплексного метода расчёта цепи, обусловлен тем что в выражениях отсутствует время.

Комплексное сопротивление.

= =-1 сопротивление на комплексной плоскости можно представить точкой координаты которой представлены координатами радиуса вектора и углом между действительной осью и радиус вектора. 1) =z<φ полярная форма записи 2) =R+jx алгебраическая форма записи 3) x=zsinφ, R=zcosφ =zcosp+jzsinφ тригонометрическая форма записи Формула Эйлера =cosφ+jsinφ Используя формулу Эйлера можно из тригонометрической формы перейти к показательной.

Коэффициент мощности.

В основном существующие электрические цепи имеют активно-индуктивный характер, поэтому ток отстаёт от напряжения. (1) Величнина - значение мощности. Из (1) (2) Из (2) следует что ток в подводящих проводах зависит от . При ток и напряжение ( Ток в проводящих проводах min. Потеря мощности в проводах если I увеличивается в 2 раза, а потеря в проводах увеличивается в 4 раза.

Для уменьшения угла параллельно нагрузке включаются конденсаторы.

Ветвь с конденсатором является чисто ёмкостной, поэтому ток в данной ветви опережает напряжение на 90 градусов. Меньшее напряжение отстаёт на , это уменьшает потерю мощности в проводах.

В реальных цепях находится в пределах от 0,6 до 1. - создаёт контур в котором конденсаторы являются накопителем энергии, когда ток уменьшается с увеличением энергии, накопленная энергия в конденсаторе отдаётся в нагрузку, контура от этого остаются последовательными.

Мощность 3-х фазовой цепи.

Активная мощность определяется одной из фаз (1) (1)= для фазовой S= S= «звезда», аналогичное выражение может быть получено и в схеме треугольник.

Мощность. а) На сопротивлении R возьмём i= , φ=0 запишем через действующее значение i= (1) для напряжения: U=i*R= (2) p=iu= = (3) построим временные диаграммы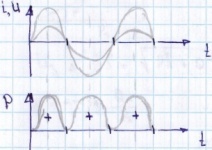 Из графика для мощности и формулы (3) следует, что мощность на R пульсирует с 2-ой частотой всегда положительно.

Определим возьмём t= . 𝝎t= . . P=2 Энергия которая выделяется наR определяется площадью находящейся под кривой. Средняя мощность за период называется активной мощностью обозначается =2 равна произведению действующих значений тока и напряжений. б) На индуктивности L, согласно векторным диаграммам сопротивление на L опережает ток на 90 градусов. Имеем i= (1) φ=0 (2) P=i

(3) Построим временные диаграммы.

Из временной диаграммы для мощности и формулы (3) следует, что Р пульсирует и с 2-ой за частотой за период 4 раза меняет знак. Среднее значение мощности за период =0. Для количественной оценки мощности на индуктивности вводят понятие размерность вар (вольт-амперно-реактивная)

в) В конденсаторе С аналогична мощности на индуктивности изменяется мощность на С то есть пульсирует с 2-ой частотой. Количественная характеристика вар.

Нелинейные элементы.

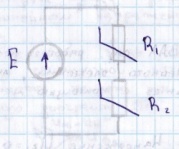
Характеризуются ВАХ. Расчёт электрических цепей проводится в основном графическим способом. Нелинейные элементы представлены своими ВАХ характеристиками. 1,2 – ВАХ нелинейн. сопр. Необходимо определить ток в цепи и падения напряжения на нелинейных элементах. Для определения строится суммарная ВАХ цепи, при выбранных значениях тока. Выбираем токи 1,2,3 и складываем соответственно абсциссы напряжений из каждой ВАХ. Режим работы цепи при заданном Е получается путём нанесения на ось напряжения источника питания

Вторым способом определения рабочего режима цепи является следующее: из точки на оси напряжений на оси Е строится вторая ВАХ. Пересечение характеристик в точке А позволяет определить

Рассмотрим расчёт цепи содержащей линейные и нелинейные сопротивления. 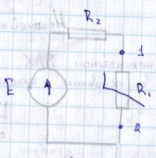Нелинейные сопротивления заданы своей ВАХ определения рабочего режима определяется наложением на ВАХ нелинейного элемента, линейной характеристики сопротивления R. Характеристика строится с помощью методов замыкания и холостого хода (ХХ). 1 Опыт короткого замыкания. Напряжение (закоротили) 2 Опыт (ХХ). Цепь разрывается на клеммах 1 и 2 U=E характеристика между точками 3 и 4 представляет собой характеристику линейного элемента. Пересечение данной характеристики с характеристикой определяет рабочее движение системы.

Параллельное соединение пассивных элементов.

Примем что - имеет активно индуктивный характер; - активно емкостной. Так как напряжение прикладываемое к цепи, одно и тоже совмещают вектор напряжения с осью абсцисс. Складывая вектора и находим ток . Используя проекции тока на оси координат и получаем ∆ тока. Φ=arctg так как ток отстаёт от напряжения, напряжение опережает ток, то характер цепи активно индуктивный.

Переходные процессы в электро цепях.

Законы коммутации. При переключении в электрических цепях возникают переходные процессы. Обусловлено тем, что реактивные элементы конденсатор и индуктивность обладают способностью накапливать энергию электрического поля. Данная энергия не может мгновенно рассеяться перейти в другие виды, требуется конечное время. Для определения установившихся режимов составляются и решаются дифференциальные уравнения. Уравнения составляются с использованием законов Кирхгофа, методом контурных токов, узловых потенциалов. Для определения постоянных интегрирования используют законы коммутации:

1-ый закон: ввиду непрерывности потока сцепления ток в индуктивности до коммутации равен току индуктивности после коммутации. .

2-ой закон: ввиду непрерывности заряда напряжение на конденсаторе до коммутации равно напряжению после коммутации