6. Классы точности приборов.

Класс точности средства измерения определяет пределы допускаемых основной и дополнительной погрешностей. Эти пределы выражаются в форме приведенной относительной, относительной или абсолютной погрешностей. Если аддитивная погрешность средства измерений преобладает над мультипликативной, то класс точности выражается в виде приведенной относительной погрешности

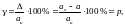
где р – отвлеченное положительное число, выбираемое из ряда (n = 1, 0, -1, -2, -3…). Для аналоговых приборов обычно р принимает значения 0,05; 0,1; 0,2; 0,5; 1; 1,5; 2,5; 4.

Если мультипликативная погрешность средства измерения преобладает над аддитивной, то класс точности выражается через относительную погрешность

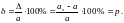
Для средств измерений с аддитивной и мультипликативной погрешностями класс точности выражается двучленной формулой

где и 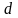- числа из приведенного выше ряда, причем , 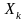- конечное значение диапазона измерений прибора, - измеренное значение. Обычно такой способ выражения класса точности используется для цифровых приборов, многозначных мер и приборов сравнения.

У аналоговых приборов обозначение класса точности выносится на лицевую панель. Если класс точности равен относительной приведенной погрешности, то класс точности обозначается в виде числа из приведенного выше ряда, например, 0,5. Если шкала прибора существенно неравномерная, то класс точности обозначается в виде числа с галочкой, например 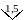, а если класс точности выражается через относительную погрешность, то число из ряда заключается в скобки, например (2,5) или окружность.

Для средств измерений с аддитивной и мультипликативной погрешностями класс точности выражается в виде дроби 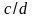, например 0,02/0,01.

7. Погрешности измерений.

Погрешности измерения можно разделить на три класса:

а) систематические; б) случайные; в) промахи.

К систематическим погрешностям относятся:

• инструментальные погрешности, которые, в свою очередь, складываются из приборной погрешности (класс точности) и погрешности от взаимодействия средства измерения с источником сигнала (зависит от входного сопротивления прибора);

• дополнительные погрешности из-за влияния внешних факторов (температура, магнитное поле и т. п.);

• личные погрешности, вызываемые индивидуальными особенностями наблюдателя;

• погрешности метода измерений.

Например, погрешность от взаимодействия средства измерения с источником сигнала при измерении тока в цепи с сопротивлением 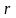и сопротивлении амперметра 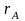равна:

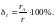
Погрешность от взаимодействия средства измерения с источником сигнала при измерении напряжения на участке цепи сопротивлением и сопротивлении вольтметра равна:

Эти формулы применимы и для измерения мощности и энергии электрического тока.

Приборная погрешность зависит от класса точности. Если класс точности прибора выражается через приведенную погрешность , то относительная погрешность показания прибора будет равна для амперметра

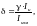
где - показание амперметра, - его номинальное значение.

Аналогично и для вольтметра

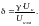
Если класс точности выражается через относительную погрешность 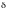, то погрешность показания равна классу точности прибора.

Дополнительные погрешности, так же относящиеся к систематическим инструментальным погрешностям, обусловлены отклонением условий измерений от нормальных.

Так, например, в схемах амперметров с шунтами, так как шунты делают из манганина (сопротивление манганина практически не зависит от температуры), приходится применять схемы температурной компенсации. В простейшем случае последовательно с рамкой включают сопротивление r₁ из манганина, рис. 1.

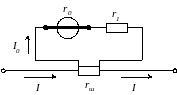
Рис. 1.

Тогда температурный коэффициент сопротивления цепи рамки уменьшится и температурная погрешность будет определяться формулой

где β₀ —температурный коэффициент сопротивления цепи рамки;

r₀ — сопротивление рамки, пружинок и соединительных проводов;

r_ш — сопротивление шунта;

r₁ — добавочное сопротивление из манганина;

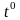; - температура во время измерения.

В приборах высокого класса точности применяют последовательно-параллельную схему температурной компенсации.

При отсутствии температурной компенсации

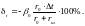
Температурная погрешность магнитоэлектрических вольтметров определяется формулой

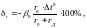
где r_Д - добавочное сопротивление из манганина.

Из формулы видно, что температурную погрешность вольтметра можно уменьшить, увеличивая добавочное сопротивление из манганина.

Для электромагнитных и электродинамических вольтметров температурная погрешность зависит от температурного коэффициента момента пружин и температурного коэффициента сопротивления катушек и определяется формулой

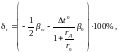
где - температурный коэффициент момента пружинок (он отрицателен и составляет 0,20,3% на 10°С).

Второй член этого выражения зависит от предела измерения прибора. Наибольшей погрешностью обладает вольтметр на самом низком пределе измерения, т.к. 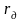в этом случае минимально.

В электродинамических амперметрах с последовательной схемой соединения катушек и в электромагнитных амперметрах температура влияет только на упругие свойства пружин. Поэтому температурная погрешность их не превышает ±0,2% на 10°С и не требует специальных способов компенсации.

На электродинамические и электромагнитные вольтметры существенное влияние оказывает частота. Главной причиной расхождения их показаний на постоянном и переменном токе является наличие индуктивного сопротивления .

Частотная погрешность при переходе от постоянного тока к переменному рассчитывается как:

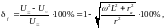
где r – сопротивление вольтметра на постоянном токе;

r_а – активное сопротивление цепи вольтметра на переменном токе.

При частотах до 2000 Гц, на которых работают эти приборы, можно считать отличие 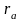и , обусловленное вихревыми токами, в толще меди обмотки и окружающих металлических частях пренебрежимо малым. Тогда, принимая r_а r, получим:

или

Отклонение подвижной части выпрямительного прибора пропорционально средневыпрямленному значению протекающего через него тока. Поэтому измерить действующее значение переменного тока можно только в том случае, если известен коэффициент формы кривой переменного тока. Обычно шкалы выпрямительных приборов градуируются в действующих значениях при синусоидальной форме кривой, умножая для этого показания прибора на коэффициент формы =1,11 (так как для синусоиды ).

Если формы кривой отличаются от синусоидальной, в показаниях возникает погрешность, присущая методу измерения

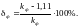
Методические погрешности обусловлены несовершенством метода измерения и, в частности, несовершенством схемы измерения. Так при косвенных измерениях сопротивления и мощности, потребляемой нагрузкой, методом амперметра и вольтметра обычно используют две схемы, рис. 2.

Рис. 2.

Погрешности измерения сопротивления ∆ и самого по схеме а) равны

где и показания приборов.

Погрешности измерения по схеме б):

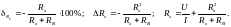
Субъективные или личные погрешности у опытных экспериментаторов обычно малы и ими пренебрегают по сравнению с другими составляющими суммарной систематической погрешности. Принято считать, что эта погрешность Δ_отс,п (погрешность отсчитывания) не превышает 20% от постоянной прибора, т.е.