22) Дифференцирование параметрических функций

Если функция задана параметрически    ее производную можно найти по формуле    Эта формула применима и для случая x = t, тогда она превращается в тождество.

Алгоритм:

1. Найти отдельно x_t'.

2. Найти отдельно y_t'.

3. Подставить полученные выражения в формулу для y_x'. 

4. Если это возможно, в полученнм выражении y_x' избавиться от t. Но это получается не всегда.

Для случая, если выражения x(t) и y(t) простые, удобнее сразу подставить их в одну из формул  y_x' = dy(t) / dx(t) или, если разделить числитель и знаменатель в правой части на dt,  y_x' = y_t' / x_t'

23) Гиперболи́ческие фу́нкции — семейство элементарных функций, выражающихся через экспоненту и тесно связанных с тригонометрическими функциями.

Гиперболические функции задаются следующими формулами:

гиперболический синус:

гиперболический косинус:

гиперболический тангенс:

гиперболический котангенс:

гиперболические секанс и косеканс:

Производные этих функций имеют вид

Ниже приводятся производные других (прямых и обратных) гиперболических функций.

24) Теорема(Ролля) Пусть функция y = f(x) непрерывна на отрезке , дифференцируема на интервале (a, b) и f(a) = f(b). Тогда существует число такое, что f ' (c) = 0.

Доказательство. Так как функция y = f(x) непрерывна на отрезке , то она на этом отрезке достигает своего наибольшего и своего наименьшего значения.

Обозначим

Если M = m, то f(x) = const . Следовательно, f '(x) = 0 для любого , и теорема для данного случая верна. Пусть теперь M≠m. Пусть M>f(a)=f(b). Тогда найдется число такое, что f(c)=M. При этом имеют место неравенства

Переходя к пределу, получаем

Если при M ≠ m выполнены равенства M = f(a) = f(b), тогда m < f(a) = f(b).

Рассмотрим функцию y = g(x) = - f(x).

Для этой функции и - m > g(a) = g(b).

Из доказанного выше следует, что существует число такое, что g ' (c) = 0. Так как g ' (c) = - f(c), то f(c) = 0 . Теорема доказана.

Теорема Коши(об отношении приращения двух функций)

Пусть функции y = f(x), y = g(x) непрерывны на отрезке и дифференцируемы на интервале (a, b), причем g ' (x) ≠ 0 на (a, b).

Тогда существует число такое, что

Доказательство. Заметим, что g(b) ≠ g(a). (Если g(b) = g(a), то, по теореме Ролля, существует число такое, что g ' (c) = 0.)

Введем обозначение: .

Рассмотрим функцию , которая непрерывна на , дифференцируема на (a, b) и F(a) = F(b) = 0, т.е. функция F удовлетворяет условиям теоремы Ролля.

Следовательно, существует число такое, что F ' (c) = 0.

Так как . Теорема доказана.

Теорема Лагранжа (о конечных приращениях)

Пусть функция y = f(x) непрерывна на отрезке и дифференцируема на интервале (a, b).

Тогда существует число , такое, что .

Доказательство. Рассмотрим вспомогательную функцию

Эта функция непрерывна и дифференцируема в промежутке   , а на его концах принимает одинаковые значения:

Тогда     удовлетворяет всем условиям теоремы Ролля и, следовательно, существует точка   , в которой производная функции     равна нулю:

      Следствие 1. В частном случае, когда   , из теоремы Лагранжа вытекает, что существует точка   , в которой производная функции    равна нулю:   . Это означает, что теорема Лагранжа является обобщением теоремы Ролля.        Следствие 2. Если     во всех точках некоторого промежутка   , то    в этом промежутке

25) Теорема (правило Лопиталя). Пусть функции f(x) и g(x) дифференцируемы в некоторой окрестности точки a, за исключением, быть может, самой точки a, и пусть или . Тогда, если существует предел отношения производных этих функций , то существует и предел отношения самих функций f(x)/g(x) при x→а, причем

Таким образом, коротко правило Лопиталя можно сформулировать следующим образом: предел отношения двух бесконечно малых или двух бесконечно больших величин равен пределу отношения их производных.

Замечание. Отметим, что формула справедлива только в том случае, если предел, стоящий справа, существует. Может случиться, что предел, стоящий слева существует, в то время как предел, стоящий в правой части равенства, не существует.

Неопределенности типа 

Пусть заданы две функции f (x) и g (x), такие, что

В этом случае говорят, что функция   имеет неопределенность типа   в точке x = a. Чтобы найти предел при x = a когда функция   содержит неопределенность  , нужно разложить на множители числитель и/или знаменатель и затем сократить члены, стремящиеся к нулю.  Примечание: В данном разделе при вычислении пределов не используется правило Лопиталя. 

Неопределенности типа 

Пусть две функции f (x) и g (x) обладают свойством

где a является действительным числом, либо стремится к + ∞ или − ∞. Говорят, что в этом случае функция   имеет в точке a неопределенность типа  . Для вычисления предела в этой точке необходимо разделить числитель и знаменатель на x в наивысшей степени. 

Неопределенности типа 

Неопределенности этих типов сводятся к рассмотренным выше неопределенностям типа   и  . 

26) Определение возрастающей функции.

Функция y = f(x) возрастает на интервале X, если для любых   и   выполняется неравенство  . Другими словами – большему значению аргумента соответствует большее значение функции. Определение убывающей функции. Функция y = f(x) убывает на интервале X, если для любых   и   выполняется неравенство  . Другими словами – большему значению аргумента соответствует меньшее значение функции.

Теорема: Достаточный признак возрастания функции. Если f’(x)>0, (a,b), то f(x) возрастает на [a,b].

Док-во:

возьмем x1, x2 [a,b]: x1<x2 => f(x2)>f(x1)

применим т. Лангранжа f(x) на [x1,x2]

по этой теореме f(x2)-f(x1)=f’(c)(x2-x1)>0 => f(x2)>f(x1).Замечание: данные условия не являются необходимыми.

Теорема: достаточный признак убывания функции. Если f’(x)<0 на (a,b), то f(x) убывает на [a,b].

Док-во 1: подобно предыдущему.

Док-во 2: g(x)=-f(x),тогда g’(x)=-f’(x)>0

=> g(x) - возрастает => f(x) – убывает.

Несложно показать, что если функция возрастает (убывает) на [a,b], то ее произв. не отрицат.(положит.) на (a,b).

f(x) возрастает: [a,b]=>f’(x)0 (a,b).

27) экстремума функций.Определение: точка x0 называется точкой max (min) если существует такая окрестность данной точки, что в x0 функция принимает наибольшее (наименьшее) значение.

Точка х0 наз. точкой экстремума, если эта точка max или min данной функции.

Теорема: Необходимый признак экстремума функции.

Если х0 точка экстремума f(x), то :

1). Либо не существует f’(x0)

2). Либо f’(x0)=0

Доказательство:

1). Не существует f’(x0)

2). Существует f’(x0) - по т. Ферма f’(x0)=0

Замечание: данные условия не являются достаточными.

Теорема 1. (Необходимое условие существования экстремума.) Если дифференцируемая функция y=f(x) имеет в точке x= x0 экстремум, то ее производная в этой точке обращается в нуль.

Доказательство. Пусть для определенности в точке x0 функция имеет максимум. Тогда при достаточно малых приращениях Δx имеем f(x0+ Δx)<f(x0), т.е. Но тогда

Переходя в этих неравенствах к пределу при Δx→ 0 и учитывая, что производная f '(x0) существует, а следовательно предел, стоящий слева, не зависит от того как Δx → 0, получаем: при Δx → 0 – 0 f'(x0) ≥ 0 а при Δx → 0 + 0 f'(x0) ≤ 0. Так как f '(x0) определяет число, то эти два неравенства совместны только в том случае, когда f '(x0) = 0.

Теорема: Первый достаточный признак экстремума функции.

Если f’(x)>0 на интервале (x0-б,х0) и f’(x)<0 на интервале (х0,x0+б) т.е. меняет знак с плюса на минус при переходе на точку х0, т.е. х0 – точка максимума f(x), а если же меняет знак с минуса на плюс, то х0 – точка минимума.

Доказательство:

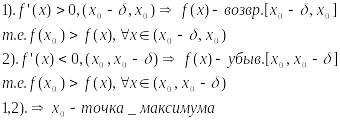
Теорема: Второй достаточный признак максимума функции.

Если f(x) имеет непрерывную вторую производную в окрестности точки х0, и:

1). f’(x0)=0 2). f’’(x0)<0

то х0 точка максимума (аналогично, если f’’(x0)<0, то х0 – точка минимума)

Док-во: Возьмем окрестность, где вторая производная сохраняет знак и запишем формулу Тейлора 1-го порядка для х из данной окрестности.

28) График функции y=f(x) называется выпуклым на интервале (a; b), если он расположен ниже любой своей касательной на этом интервале.

График функции y=f(x) называется вогнутым на интервале (a; b), если он расположен выше любой своей касательной на этом интервале.

Достаточное условие вогнутости ( выпуклости ) функции.

Пусть функция f ( x ) дважды дифференцируема ( имеет вторую производную ) на интервале ( a, b ), тогда: если f '' ( x ) > 0 для любого x ( a, b ), то функция f ( x ) является вогнутой на интервале ( a, b );

если f '' ( x ) < 0 для любого x ( a, b ), то функция f ( x ) является выпуклой на интервале ( a, b ) .

Точка, при переходе через которую функция меняет выпуклость на вогнутость или наоборот, называется точкой перегиба. Отсюда следует, что если в точке перегиба x0 существует вторая производная f '' ( x0 ), то f '' ( x0 ) = 0.

Точка перегиба функции внутренняя точка x0 области определения f такая что f непрерывна в этой точке, и x0 является одновременно концом интервала строгой выпуклости вверх и концом интервала строгой выпуклости вниз.

В этом случае точка (x0;f(x0)) является точкой перегиба графика функции, т. е. график функции f в точке (x0;f(x0)) «перегибается» через касательную к нему в этой точке: при x < x0 касательная лежит под графиком f, а при x > x0 — над графиком f (или наоборот)

Необходимое условие существования точки перегиба: если функция f(x), дважды дифференцируемая в некоторой окрестности точки x0, имеет в x0 точку перегиба, то f''(x0) = 0.

Достаточное условие существования точки перегиба: если функция f(x) в некоторой окрестности точки x k раз непрерывно дифференцируема, причем k нечётно и , и f(n) = 0 при n = 2,3,...,k − 1, а , то функция f(x) имеет в x0 точку перегиба.

29) Асимптоты.

Часть графика называется бесконечной ветвью если при движении точки по этой части, расстояние между ей и началом координат стремится к бесконечности.

Прямая называется асимптотой бесконечной ветви графика функции, если при удалении точки от начала координат по этой ветви, расстояние до данной прямой стремится к нулю.

Теорема 1: x=a (вертикальная прямая) – является асимптотой для бесконечно вертикальной ветви графика функции y=f(x), тогда когда f(x), при xa.

Теорема 2: Критерий существования наклонной асимптоты прямая y=kx+b является асимптотой для правой (левой) ветви графика функции тогда, когда существует предел при :

Док-во: Точка M0(x0,y0) и прямая

L: Ax+By+Cz=0, то расстояние

Пусть y=kx+b

асимптота =>

d(M,l)0=>kx-f(x)+b0

тогда f(x)-kxb

при x+

существует предел:

Теорема: Необходимый признак существования наклонной асимптоты. Если прямая l: y=kx+b –

наклонная асимп. для правой наклонной ветви, то:

30) Чтобы найти наибольшее или наименьшее значение функции на отрезке, нужно исследовать поведение функции на данном отрезке с помощью производной.

Для этого мы следуем известному алгоритму:

1. Находим ОДЗ функции.

2. Находим  производную функции

3. Приравниваем производную  к нулю

4. Находим промежутки, на которых производная сохраняет знак,  и по ним определяем промежутки возрастания и убывания функции:

Если на промежутке I производная функции  , то функция   возрастает на этом  промежутке.

Если на промежутке I производная функции  , то функция   убывает на этом промежутке.

5. Находим точки максимума и минимума функции.

В точке максимума функции производная меняет знак с «+» на «-».

В точке минимума функции производная меняет знак с «-» на «+».

6. Находим значение функции в концах отрезка,

• затем сравниваем значение функции в концах отрезка и в точках максимума, и выбираем из них наибольшее, если нужно найти наибольшее значение функции

• или   сравниваем значение функции в концах отрезка и в точках минимума, и выбираем из них наименьшее, если нужно найти наименьшее значение функции

31) Примерная схема исследования графика функции.

1).Область определения.

2).Четность (нечетность), переодичность, точки пересечения и др.

3). Непрерывность, точки разрыва, вертикальные асимптоты.

4). Исследование на убывание (возвр.) в точках экстремума.

5). Исследование на выпуклость.

6). Построение графика функции.