2. Табличный способ: функция задается с помощью таблицы.

3. Описательный способ: функция задается словесным описанием

4. Графический способ: функция задается с помощью графика

5. Пределы на бесконечности

6. Пределы функции на бесконечности

7. Элементарные функции:

8. 1) степенная функция y=xⁿ

9. 2) показательная функция y=a^x

10. 3) логарифмическая функция y=log_ax

11. 4) тригонометрические функции y=sin x, y=cos x, y=tg x, y=ctg x

12. 5) обратные тригонометрические функции y=arcsin x, y=arccos x, y=arctg x, y=arcctg x.

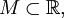13. Пусть и 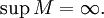Тогда система множеств

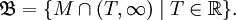
14. является фильтром и обозначается 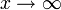или Предел 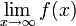называется пределом функции f при x стремящемся к бесконечности.

2) Число А называется пределом функции y=f(x) в точке х₀, если для любой последовательности допустимых значений аргумента x_n, n€N (x_n≠x₀), сходящейся к х₀

(т.е. ), последовательность соответствующих значений функции f(x_n), n€N, сходится к числу А, т.е. . Геометрический смысл предела этой функции, что для всех точек х, достаточно близких к точке х₀, соответствующие значения функции как угодно мало отличается от числа А.

Односторонние пределы.Считается, что х стремится к х₀ любым способом: оставаясь меньшим, чем х₀ (слева от х₀), большим, чем х₀ (справа от х₀), или колеблясь около точки х₀.Число А₁ называется пределом функции y=f(x) слева в точке х₀, если для любого ε<0 существует число σ=σ(ε)>0 такое, что при х€(x₀-σ;x₀), выполняется неравенство |f(x)-A₁|<ε

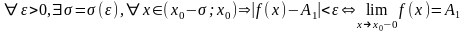
Пределом функции справа называется

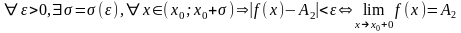
Свойства пределов.

1) если предел функция равна этому числу плюс б.м.

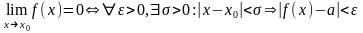
ε – сколь угодно малое число

|f(x)-a|=α; f(x)=a+ α2) сумма конечного числа б.м. чисел есть б.м. число 3) предел произведения равен произведению пределов

4) константы можно выносить за знак предела5)

Число b называется пределом функции в точке а, если для любой   – окрестности точки b существует   – окрестность точки а.

      

 – предел функции при  , равный b.

Число b называется пределом функции при неограниченном возрастании аргумента  . Для любого  существует такое N, и если  , то  .

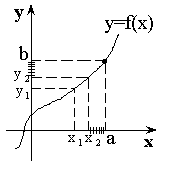3) Рассмотрим ряд натуральных чисел: 1, 2, 3, … , n –1, n, … .

Если заменить каждое натуральное число n в этом ряду некоторым числом u_n , следуя некоторому закону, то мы получим новый ряд чисел:

u₁ , u₂ , u₃ , …, u_n - 1 , u_n , …, кратко обозначаемый { u_n }

и называемый числовой последовательностью. Величина u_n называется общим членом последовательности. Обычно числовая последовательность задаётся некоторой формулой u_n = f(n), позволяющей найти любой член последовательности по его номеру n; эта формула называется формулой общего члена. Заметим, что задать числовую последовательность формулой общего члена не всегда возможно; иногда последовательность задаётся путём описания её членов

Удобным инструментом при изучении предельных переходов является понятие бесконечно малой последовательности. Последовательность { n } называется бесконечно малой, если _n 0 при n . Основные свойства бесконечно малых последовательностей:

1. Сумма и разность бесконечно малых последовательностей { n } и { 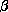n } есть бесконечно малая последовательность.

2. Б\м последовательность – ограниченна.

3. Произведение бесконечно малой последовательности на ограниченную последовательность есть бесконечно малая последовательность.

4. Для того, чтобы последовательность { xn } сходилась к некоторому числу а необходимо и достаточно, чтобы существовала бесконечно малая последовательность { an }, такая, что для всех n выполнялось xn = а + an

4)

 Функция одной переменной. Определение предела функции в точке по Коши.Число bназывается пределом функции у = f(x) при х, стремящемся к а (или в точке а), если для любого положительного числа  существует такое положительное число , что при всех х ≠ а, таких, что |x – a | < , выполняется неравенство | f(x) – a | <  .

Определение предела функции в точке по Гейне. Число b называется пределом функции у = f(x) при х, стремящемся к а (или в точке а), если для любой последовательности {x_n}, сходящейся ка (стремящейся к а, имеющей пределом число а), причем ни при каком значении n х_n ≠ а, последовательность {y_n = f(x_n)} сходится к b.

Данные определения предполагают, что функция у = f(x) определена в некоторой окрестноститочки а, кроме, быть может, самой точки а.

Определения предела функции в точке по Коши и по Гейне эквивалентны: если число b служит пределом по одному из них, то это верно и по второму.

Указанный предел обозначается так:

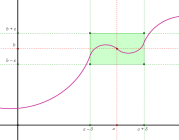
Геометрически существование предела функции в точке по Коши означает, что для любого числа  > 0 можно указать на координатной плоскости такой прямоугольник с основанием 2 > 0, высотой 2 и центром в точке (а; b), что все точки графика данной функции на интервале (а–; а + ), за исключением, быть может, точки М(а; f(а)), лежат в этом прямоугольнике – см. рис.:

5) Исчисление бесконечно малых — вычисления, производимые с бесконечно малыми величинами, при которых производный результат рассматривается как бесконечная суммабесконечно малых. Исчисление бесконечно малых величин является общим понятием для дифференциальных и интегральных исчислений, составляющих основу современной высшей математики. Понятие бесконечно малой величины тесно связано с понятием предела.