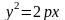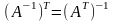1)Определители 3-го порядка.Св-ва. 9 элементов a_ij, где i-номер строка, а j-номер столбца, располагаются в квадратную таблицу, называемую квадратной матрицей третьего порядка. Ей можно поставить в соответствие число, которое называется определителем 3-го порядка. Свойство1. Важным свойством определителей является следующее соотношение: det A = det A^T; Свойство 2.det ( A  B) = det A  det B.Свойство 3. det (AB) = detAdetB

Свойство 4. Если в квадратной матрице поменять местами какие-либо две строки (или столбца), то определитель матрицы изменит знак, не изменившись по абсолютной величине.Свойство 5. При умножении столбца (или строки) матрицы на число ее определитель умножается на это число.Определение: Столбцы (строки) матрицы называются линейно зависимыми, если существует их линейная комбинация, равная нулю, имеющая нетривиальные (не равные нулю) решения.Свойство 6. Если в матрице А строки или столбцы линейно зависимы, то ее определитель равен нулю.Свойство 7. Если матрица содержит нулевой столбец или нулевую строку, то ее определитель равен нулю. (Данное утверждение очевидно, т.к. считать определитель можно именно по нулевой строке или столбцу.)Свойство 8. Определитель матрицы не изменится, если к элементам одной из его строк(столбца) прибавить(вычесть) элементы другой строки(столбца), умноженные на какое-либо число, не равное нулю.Свойство 9. Если для элементов какой- либо строки или столбца матрицы верно соотношение: d = d₁  d₂ , e = e₁  e₂ , f = f₁  f₂ , то верно:

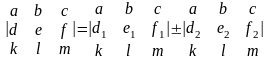
2) Матрица – таблица, содержащая m строк и n столбцов.

Матрица размера n x n называется квадратной матрицей n-го порядка.

Квадратную матрицу размера n x n называют матрицей n-го порядка.

Квадратная матрица, у которой все элементы, кроме элементов главной диагонали, равны нулю, называется диагональной.

Диагональная матрица, у которой каждый элемент главной диагонали равен единице, называется единичной (обозначается буквой E).

Квадратная матрица называется треугольной, если все элементы, расположенные по одну сторону от главной диагонали, равны нулю.

Матрица, все элементы которой равны нулю, называется нулевой (обозначается буквой О).

Матрица ступенчатого вида – матрица, у которой все члены ниже главной диагонали равны нулю.

Элементарные преобразования матриц:

1. Перестановка местами двух параллельных рядов матрицы

2. Умножение всех элементов ряда на число, отличное от нуля

3. Прибавление к элементам одного ряда соответствующих элементов параллельного ряда, умноженных на число.

4. Вычеркивание строки из нулей.

Свойства матриц:

1. A+B=B+A (коммутативный закон сложения)

2. A+(B+C)=(A+B)+C (ассоциативный закон)

3. A+0=A ( закон поглощения нуля)

4. α∙A=A∙α (коммутативный закон умножения)

5. 1∙A=A(закон поглощения единицы)

6. α∙(A+B) =α∙A+ α∙B(дистрибутивный закон)

7. (α+β)∙A= α∙A+ β∙A

8. α∙( βA)= (α β)∙A

3) Рангом(обозначается r,r(A),rang(A)) матрицы называется наибольший из порядков миноров данной матрицы, отличных от нуля.

<=>

Рангом матрицы называется число линейно независимых строк.

Способы нахождения ранга матрицы:

1. Нахождение наибольшего(базисного) минора матрицы.

2. Приведение к каноническому виду(с помощью элементарных преобразований).

4) Опр.1.Строки a1; a2; a3;...;an называются линейно независимыми если равенство 1a1+2a2+...+nan=0 возможно только при всех =0.

Опр.2.Строки a1; a2; a3;...;an называются линейно зависимыми если это равенство возможно хотя бы при одном ≠0.

Опр.3.Строки линейно зависимы если одна из строк является линейной комбинацией остальных.

Опр1<=>Опр3

5) Базисным минором матрицы называется любой её ненулевой минор максимального порядка.Теорема. В произвольной матрице А каждый столбец (строка) является линейной комбинацией столбцов (строк), в которых расположен базисный минор.Таким образом, ранг произвольной матрицы А равен максимальному числу линейно независимых строк (столбцов) в матрице. Если А- квадратная матрица и detA = 0, то по крайней мере один из столбцов – линейная комбинация остальных столбцов. То же самое справедливо и для строк. Данное утверждение следует из свойства линейной зависимости при определителе равном нулю.

6) Системой линейных алгебраических уравнений, содержащей m уравнений и n неизвестных, называется система вида

Где числа aij называются коэффициентами системы, числа bij – свободными членами.

Система называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет ни одного решения.

Совместная называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.

Если свободные члены всех уравнений равны нулю, то система называется однородной.

7)Теорема совместности системы(Кронкера-капелли):Сист.лин.урав. совместна только когда ранг основной матрицы системы равен рангу расшириной матрицы. RangA- Rang A(вектр)=R. 1)если ранг матрицы равен числу неизвестных R=n то слу имеет единств. Решение.2)если R<n то ∞ решений.

8)если система определенна то находим единственное решение, а если не определенна то в ответ записываем все множество решений.

3 распространненых метода нахождения решений СЛУ:Гауса, Крамера,Матричный.

9) метод Гаусса может быть применен к системам линейных уравнений с произвольным числом уравнений и неизвестных. Суть метода заключается в последовательном исключении неизвестных.

Сначала следует привести систему к треугольному (ступенчатому) виду, а затем ступенчато решить.

10) Метод Крамера

11) Матричный метод

12)Обратная матрица

1. 

2. 

3. 

Для того чтобы матрица имела обратную достаточно того, чтобы она была невырождена.

Нахожд.1)считаем опред.2)находим матрицу состоящиую из алгебр допл А*3)А*т 4)А(-1)1/А*А*т

13) Система однородных уравнений всегда имеет нулевое решение. Если ранг матрицы меньше числа неизвестных, то система имеет бесчисленное множество решений. Для того, чтобы система имела ненулевые решения, необходимо, чтобы ее определитель был равен нулю.

14) Векторы, действия над ними.Определение. Вектором называется направленный отрезок (упорядоченная пара точек). К векторам относится также и нулевой вектор, начало и конец которого совпадают.Определение. Длиной (модулем) вектора называется расстояние между началом и концом вектора. Определение. Векторы называются коллинеарными, если они расположены на одной или параллельных прямых. Нулевой вектор коллинеарен любому вектору.Определение. Векторы называются компланарными, если существует плоскость, которой они параллельны. Коллинеарные векторы всегда компланарны, но не все компланарные векторы коллинеарны. Определение. Векторы называются равными, если они коллинеарны, одинаково направлены и имеют одинаковые модули.Всякие векторы можно привести к общему началу, т.е. построить векторы, соответственно равные данным и имеющие общее начало. Из определения равенства векторов следует, что любой вектор имеет бесконечно много векторов, равных ему.Определение. Линейными операциями над векторами называется сложение и умножение на число.Суммой векторов является вектор - 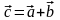Произведение - , при этом 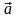коллинеарен .Вектор сонаправлен с вектором (  ), если  > 0.Вектор противоположно направлен с вектором (  ), если  < 0.Линейные операции над векторами в координатах.Пусть заданы векторы в прямоугольной системе координат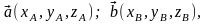 тогда

15) Произведением ненулевого вектора a на отличное от нуля число x называется такой вектор xa, для которого выполняются два условия:

его длина равна произведению длины вектора a на модуль числа x, т.е. выполняется равенство |x·a| = |x|·|a|;

он сонаправлен с вектором a, если x > 0, и он направлен противоположно вектору a, если x < 0.

Если же a = 0 или x = 0, то вектор xa - нулевой.

войства операции умножения вектора на число:

1. 1 · a = a для любого вектора a.

2. (-1) · a = -a для любого вектора a.

3. Если хa = 0, то либо х = 0 , либо a = 0.

4. Если хa = уa и a ≠ 0, то х = у.

5. Если хa = хb и х ≠ 0, то a = b.

6. х(уa)=(ху)a для любого вектора a и любых чисел х и у .

16) Линейная зависимость и независимость системы векторов. Пусть имеется n векторов.

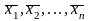
Составим линейную комбинацию:

, если система n векторов – линейно-зависима.

Если среди n векторов какие-то k линейно-зависимы, то вся система векторов является линейно-зависимой.

Если система n векторов линейно-независима, то любая часть из этих векторов будет тоже линейно-независимой.

17)Пусть система n векторов линейно-независима, а любая система n+1 векторов – линейно-зависима, тогда число n называют размерностью пространства. dimV=n

Система этих n линейно-независимых векторов называется базисом линейного пространства. Рассмотрим систему n+1 векторов.

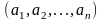Такое представление называется разложение по базису, а числа называют координатами вектора.

Разложение любого вектора в выбранном базисе - единственно.

18) Проекцией вектора на ось называется разность проекций конца вектора и его начала.

Координатами вектора b относительно базиса В называется упорядоченная тройка чисел {x, y, z}, т.ч. b=x·a1+ y·а2+z· а3.

Обозначение: b={x, y, z}_B

Замечание: Под координатами закреплённого вектора понимают координаты соответствующего ему свободного вектора.

Прямоугольная система координат (любой размерности) также описывается набором ортов, сонаправленных с осями координат. Количество ортов равно размерности системы координат и все они перпендикулярны друг другу.

В трёхмерном случае такие орты обычно обозначаются i j k. При этом в случае правой системы координат действительны следующие формулы с векторным произведением векторов:

[i j]=k ; [j k]=i ; [k i]=j .

Проекцией на ось называется длина отрезка А`B`, заключенная между ортогональными проекциями начала А и конца В вектора , взятая со знаком (+), если и с (-), если

Теорема (о проекции вектора на ось): проекция вектора на ось равна длине этого вектора, умноженной на косинус угла между векторами и осью.

Следствие: Равные вектора имеют равные проекции на одну ось.

Направленный отрезок называется ортогональной проекцией на ось

Теорема (о проекции суммы векторов): проекция суммы двух векторов на ось равна сумме проекций двух векторов на ту же ось.

Теорема (о проекции произведения скаляра на вектор): при умножении вектора на скаляр , его проекция на ось умножается на этот же скаляр

19) Декартова СК.

x - абсцисс, y – ординат, z – аппликат.

Для любого вектора   , который лежит в плоскости   , имеет место следующее разложение: .Если вектор   расположен в пространстве, то разложение по ортам координатных осей имеет вид: 

Ра́диус-ве́ктор (обычно обозначается r со стрелкой наверху или просто r) — вектор, задающий положения точки в пространстве относительно некоторой заранее фиксированной точки, называемой началом координат.  Для произвольной точки в пространстве, радиус-вектор — это вектор, идущий из начала координат в эту точку.  Длина радиус-вектора, или его модуль, определяет расстояние, на котором точка находится от начала координат, а стрелка указывает направление на эту точку пространства.  На плоскости углом радиус-вектора называется угол, на который радиус-вектор повёрнут относительно оси абсцисс в направлении против часовой стрелки.

20)Направление вектора в пространстве определяется углами  , которые вектор образует с осями координат (рис. 12). Косинусы этих углов называются направляющими косинусами вектора:  ,  ,  .

Из свойств проекций: ,  ,  . Следовательно,

Легко показать, что

1)      ;

2)     координаты любого единичного вектора совпадают с его направляющими косинусами:  .

21) )Скалярное произведение векторов, его св-ва и вычисления. Определение. Скалярным произведением векторов и называется число, равное произведению длин этих сторон на косинус угла между ними.  =   cos Свойства скалярного произведения:  =  ²;  = 0, если  или = 0 или = 0.  =  ; ( + ) =  +  ;(m ) = (m ) = m(  );Если рассматривать векторы 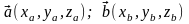в декартовой прямоугольной системе координат, то  = x_a x_b + y_a y_b + z_a z_b;Используя полученные равенства, получаем формулу для вычисления угла между векторами:

22) Векторным произведением векторов и называется вектор , удовлетворяющий следующим условиям:1) 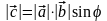, где  - угол между векторами и , 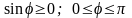2) вектор ортогонален векторам и

3) , и образуют правую тройку векторов.Обозначается: 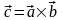или .



Свойства векторного произведения векторов:1) 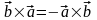;2) , если  или = 0 или = 0;3) (m ) = (m ) = m(  );4) ( + ) =  +  ;5) Если заданы векторы (x_a, y_a, z_a) и (x_b, y_b, z_b) в декартовой прямоугольной системе координат с единичными векторами 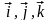, то  = 6) Геометрическим смыслом векторного произведения векторов является площадь параллелограмма, построенного на векторах и 7)физ смысл- Момент импульса мат. точки.

23) Смешанное произведение записывают в виде: .

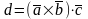Смысл смешенного произведения: сначала два вектора векторно перемножают, а затем полученный скалярно перемножают с третьим вектором. Смешанное произведение представляет собой число – число. Результат смешанного произведения – объем параллелепипеда, образованного векторами.

Свойства.

1. Смешанное произведение не меняется при циклической перестановке сомножителей:

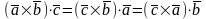
2. Смешанное произведение не изменится при перемене местами векторного и скалярного произведения.

3. Смешанное произведение меняет знак при перемене мест любых двух векторов-сомножителей.

4. Смешанное произведение трех ненулевых векторов равно нулю тогда и только тогда, когда они компланарны.

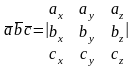
Три вектора называются компланарными, если результат смешанного произведения равен нулю.

24) Полярная система координат — двумерная система координат, в которой каждая точка на плоскости определяется двумя числами — полярным углом и полярным радиусом. Полярная система координат особенно полезна в случаях, когда отношения между точками проще изобразить в виде радиусов и углов; в более распространённой, декартовой или прямоугольной системе координат, такие отношения можно установить только путём применения тригонометрических уравнений.

Полярная система координат задаётся лучом, который называют нулевым или полярной осью. Точка, из которой выходит этот луч, называется началом координат или полюсом. Любая точка на плоскости определяется двумя полярными координатами: радиальной и угловой. 

Пару полярных координат   и   можно перевести в Декартовы координаты   и   путём применения тригонометрических функций синуса и косинуса: в то время как две декартовы координаты   и   могут быть переведены в полярную координату  :

 (по теореме Пифагора).

Для определения угловой координаты   следует принять во внимание два следующие соображения:

• Для 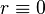 ,   может быть произвольным действительным числом.

• Для 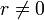 , чтобы получить уникальное значение  , следует ограничиться интервалом в 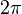 . Обычно выбирают интервал 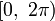  или  .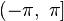

25) Переход от одной системы координат в какую-либо другую называется преобразованием системы координат.Рассмотрим два случая преобразования одной прямоугольной системы координат в другую. Полученные формулы устанавливают зависимость между координатами произвольной точки плоскости в разных системах координат.Параллельный перенос осей координатПусть на плоскости задана прямоугольная система координат Оху. Под параллельным переносом осей координат понимают переход от систе­мы координат Оху к новой системе O₁x₁y ₁, при котором меняется поло­жение начала координат, а направление осей и масштаб остаются неиз­менными.

26) Ax+By+C=0 – общее уравнение прямой

В декартовой системе координат на плоскости каждая прямая определяется уравнением 1–й степени и, обратно, каждое уравнение 1–й степени определяет прямую.

Уравнение вида Ax + By + Cz = 0 ( A² + B² ≠ 0 ) называетсяобщим уравнением прямой.

Любой вектор, перпендикулярный прямой, называетсянормальным вектором и обозначается n(вектор) 

. Например, n(вектор)  = {A, B}.

Угловым коэффициентом k прямой называется число k = tgα , где α — угол наклона прямой к оси OX (0 ≤ α < π).

Уравнение y = kx + b называется уравнением прямой с угловым коэффициентом (b — ордината точки пересечения прямой с осью OY).

   Доказательство. 1) Пусть L произвольная прямая на координатнойплоскости Оху и пусть точка   ее произвольная фиксированная точка, М(х, у) – ее текущая точка,   – ее произвольный нормальный вектор. Тогда уравнение (1) является векторным уравнением этой прямой, где   ,  .

   Расписывая скалярное произведение в координатной форме, получаем  . Раскрывая скобки и группируя, получаем

                      .

Обозначая через  , получаем отсюда равенство (2), которое и будет уравнением данной прямой.

27) Векторное уравнение прямой: [r-r₀,a]=0; a – направляющий вектор прямой, r₀ – радиус-вектор начальной точки прямой.

Ax+By+C=0 – общее уравнение прямой

Полярное уравнение: r cos(φ – λ)=p

Нормальное уравнение: x∙cos λ + y ∙sin λ – p=0

Каноническое

Вывод:

Уравнение прямой, проходящей через две данные точки:

Уравнение прямой в отрезках:

Векторное параметрическое уравнение прямой в пространстве:

Параметрические уравнения прямой в пространстве:

Каноническое уравнение прямой в пространстве:

28) Уравнение прямой, проходящей через данную точку в данном направлении: y-y0=k(x-x0­)

Будем искать уравнение прямой в виде уравнения с угловым коэффициентом: y = k · x + b. Угловой коэффициент прямой можно найти, зная угол наклона k = tg . Возьмем произвольную точку M (x, y), лежащую на этой прямой, и найдем уравнение, связывающее переменные x и y. Так как точки М и M₁ лежат на прямой, то их координаты удовлетворяют уравнению прямой:

y = k · x + b,

y₁ = k · x₁ + b.

Вычитая эти равенства, получим:

y - y₁ = k · (x - x₁) - уравнение прямой, проходящей через данную точку в данном направлении.

Уравнение прямой линии, пересекающей ось   в точке   и образующей угол   с положительным направлением оси  : Коэффициент   называется угловым коэффициентом прямой. В этом виде невозможно представить прямую, параллельную оси 

29) Взаимное расположение нескольких прямых на плоскости Две прямые, заданные уравнениями или пересекаются в точке Угол   между пересекающимися прямыми определяется формулой При этом под   понимается угол, на который надо повернуть первую прямую (заданную параметрами  ,  ,  ,   и  ) вокруг точки пересечения против часовой стрелки до первого совмещения со второй прямой.Эти прямые параллельны, если   или  , и перпендикулярны, если   или  .Любую прямую, параллельную прямой с уравнением   можно выразить уравнением   При этом расстояние между этими прямыми будет равно

Взаимное расположение двух прямых и пространстве характеризуется следующими тремя возможностями.

1. Прямые лежат в одной плоскости и не имеют общих точек — параллельные прямые.

2. Прямые лежат и одной плоскости и имеют одну общую точку — прямые пересекаются.

3. В пространстве две прямые могут быть расположены еще так, что не лежат ни в одной плоскости. Такие прямые называются скрещивающимися (не пересекаются и не параллельны).

Теорема. Если одна из двух прямых лежит в некоторой плоскости, а другая пересекает эту плоскость и точке, которая не лежит на первой прямой, то эти прямые скрещиваются.

Теорема. Через каждую из двух скрещивающихся прямых проходит только одна плоскость, параллельная другой прямой.

30) Эллипс. Определение. Вывод канонического уравнения.

Эллипсом называется

геометрическое место всех

точек плоскости, сумма

расстояний от которых до

до фокусов есть величина

постоянная, большая, чем расстояние между фокусами.

Пусть М (х;у) – произвольная точка эллипса.

Т.к. MF₁ + MF₂ = 2a

Т.к.

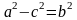
То получаем

Или

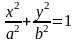
Гипербола. Определение. Вывод канонического уравнения.

Гиперболой называется множество всех точек плоскости, модуль разности расстояний от каждой из которых до фокусов есть величина постоянная.

Пусть M(x;y) – произвольная точка гиперболы. Тогда согласно определению гиперболы |MF₁ – MF₂|=2a или MF₁ – MF₂=±2a,

Парабола. Определение. Вывод канонического уравнения.

Парабола – множество всех точек плоскости, каждая из которых одинаково удалена от фокуса, и директрисы. Расстояние между фокусом и директрисой называется параметром параболы и обозначается через р>0.

Пусть M(x;y) – произвольная

точка M с F. Проведем отрезок

MN перпендикулярно

директрисе. Согласно

определению MF=MN.