Реальные газы
1. В уравнение Клайперона-Менделеева необходимо ввести поправки, учитывающие размеры молекул и взаимодействие между ними.
- уравнение
Ван-дер-Ваальса
a, b - постоянные В-q-В (учет сил взаимодействия – притяжения и размеров молекул – сил отталкивания)
Зависимость от V при постоянном на практике графически выглядит так:
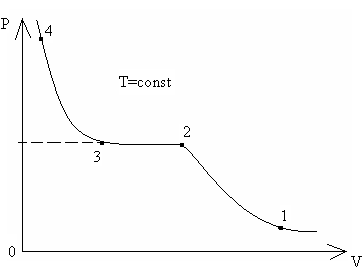
Кривая 12 описывает газообразное состояние, 23 – двухфазное (газ + жидкость), 34 – жидкое состояние вещества
2. С увеличением ширина горизонтального участка 23 уменьшается, а при некоторой температуре кр превращается в точку перегиба. В таком состоянии исчезает различие между жидкостью и газом. Такое состояние называется критическим. Соответствующее давление и объем также называются критическими.
3. Внутренняя энергия реального газа помимо кинетической энергии движения молекул должна учитывать потенциальную энергию из взаимодействия.
Для реального газа
- № 42, 452
Жидкости
1. Вследствие разницы в плотностях жидкости и пара молекулы, находящиеся на поверхности жидкости, испытывают результирующую силу, направленную вглубь жидкости. Поэтому эти молекулы обладают избыточной энергией по сравнению с молекулами, находящимися в объеме жидкости.
По этой причине жидкость принимает такую форму, при которой площадь поверхности минимальна (этим объясняется сферическая форма капель жидкости).
Коэффициентом
поверхностного натяжения называется
работа, необходимая для увеличения
площади поверхности жидкости на единицу
.
По-другому
можно определить как силу поверхностного
натяжения, действующую на единицу длины
границы раздела жидкости с другой средой
,
F
– сила,
– длина границы.
Коэффициент зависит от природы жидкости и ее температуры. С увеличением температуры уменьшается, а в критическом состоянии =0.
2. Силы поверхностного
натяжения стягивают поверхность
жидкости, поэтому давление под искривленной
поверхностью жидкости больше, чем под
плоской поверхностью. Избыточное
давление равно
– формула Лапласа.
В случае сферической
поверхности r1=r2
и
,
а для цилиндрической поверхности один
из радиусов r=
и поэтому
,
т.е. вдвое меньше, чем при сферической.
3. Из-за избыточного
лапласовского давления в тонких трубках
(капилляры) жидкость поднимается вверх
(смачивающая жидкость) или опускается
вниз (несмачивающая жидкость) по сравнению
с уровнем жидкости в широкой части
сосуда на величину
,
где ρ – плотность жидкости,
,
r
– радиус капилляра.
Твердые тела
1. Твердые тела делятся на аморфные и кристаллические. В кристаллах расположение частиц упорядоченное и этот порядок распространяется по всему объему, а в аморфных имеет место ближний порядок, т.е. он нарушается. Аморфные тела изотропны, т.е. их свойства одинаковы во всех направлениях. Кристаллы анизотропны, т.е. их свойства зависят от направления, в котором они рассматриваются.
2. Элементарная ячейка, повторением которой можно построить кристалл, называется кристаллической решеткой.
Кристаллические решетки образуют 32 класса симметрии, которые делятся на 7 систем (самая простая кубическая).
3. В зависимости от природы частиц, находящихся в узлах и на гранях кристаллической решетки, различают 4 физических типа кристаллов: атомные (например, алмаз, в узлах атомы углерода), молекулярные (лёд), ионные (поваренная соль NaCL) и металлические (металлы и сплавы).
4. В классической
физике твердое тело рассматривают как
совокупность частиц, совершающих
гармонические колебания около положения
равновесия с одинаковой полной энергий.
По такой модели молярная теплоемкость
всех твердых тел при постоянном объеме
=3R
- Закон Дюлонга и Пти, т.е. Cv=Const.
R
- универсальная газовая постоянная.
5. При низких температурах Закон Дюлонга и Пти не выполняется. Опыт показывает, что при 0 теплоемкость Cv 0. Эйнштейн положил, что осцилляторы имеют различные энергии nhv, где n=0, 1, 2... Им было вычислено среднее значение энергии осциллятора, а на его основе значение теплоемкости
- № 53, 203