Зеркала
1. Системы, отражающие падающие на них свет, называется зеркалами. В зависимости от формы отражающей поверхности зеркала бывают плоские, сферические, параболические и т.д. Ниже будут рассмотрены сферические зеркала.
2. Линия, проходящая
через вершину зеркала и центр сферической
поверхности, называется оптической
осью. Фокусное расстояние зеркала F=
,
где R
- радиус сферической поверхности. Фокус
располагается посередине между центром
сферической поверхности и вершиной
зеркала.
3. Зеркала бывают выпуклые и вогнутые (по отношению к падающему лучу света).
а) для вогнутого зеркала:
- луч света, падающий параллельно оптической оси, после отражения,
проходит через фокус;
- луч света, при падении проходящий через фокус, после отражения
идет параллельно оптической оси.
б) для выпуклого зеркала:
- луч света, падающий параллельно оптической оси, отражается так,
что его продолжение в обратную сторону проходит через фокус;
- луч света, падающий на зеркало так, что его продолжение проходит
через фокус (за зеркалом), отражается параллельно оптической оси.
4. Формула зеркала:
+
=
,
где а
и b
– расстояния от зеркала до предмета и
от зеркала до изображения, F
– фокусное расстояние.
Для вогнутого зеркала все величины положительные, для выпуклого зеркала а отрицательно, а b и F положительны.
- № 144, 391
Интерференция света
1. Когерентные волны – волны, в которых колебания совершаются с одинаковой частотой в одном направлении и с постоянной разностью фаз.
2. Интерференция – результат наложения когерентных волн, приводящий либо к усилению, либо к ослаблению налагаемых волн.
3. Амплитуда
результирующей волны при интерференции
,
где
1,
2
– амплитуды складывающихся волн, (
-
)
– разность фаз волн.
Условие max (усиление волн): - =2n , n=0, 1, 2..., условие min (ослабление волн): - =(2n-1) , n=1, 2, 3...
4. Условия max
и min
можно выразить и через разность хода
волн:
S=2n
(max),
n=0,
1, …;
S=(2n-1)
,
n=1,
2, ..., где
-
длина волны.
5. Опыт Юнга
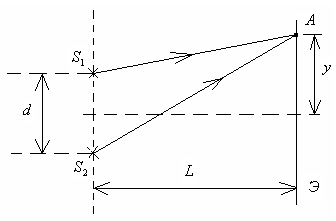
S1, S2 – когерентные источники света, Э – экран, - точка, где налагаются волны.
В точке
будет max,
если y=
,
где n=0,
1, 2… и min,
если y
=
,
где n=1,
2, …
6. При отражении света от плоской пластины (верхней и нижней граней) разность хода волн зависит от угла падения света i и толщины пластины d.
Примером интерференции света при одинаковом i, но при разных d являются кольца Ньютона.
Радиус светлого
кольца
=
,
n=1,
2, ..., а темного r
=
,
n=0,
1, ..., R
– радиус кривизны линзы.
7. В случае освещения белым светом, поверхность масляной пленки на поверхности воды окажется цветной – пример интерференции.
- № 45, 118, 172, 245, 269, 272, 450, 482
Дифракция света
1. Дифракция - отклонение от прямолинейного распространения света, выражающееся в огибании препятствий и отверстий (размеры препятствий и отверстий должны быть сравнимы с длиной волны).
2. Волновая поверхность – геометрическое место точек среды, колеблющихся в одинаковой фазе. По виду волновых поверхностей различают сферические и плоские волны.
3. Принцип Гюйгенса-Френеля: 1) каждую точку волновой поверхности, до которой дошла волна, можно рассматривать как источник вторичных волн; 2) вторичные волны когерентные, поэтому должны интерферировать.
4. Зоны Френеля – участки волновой поверхности, выбираемые таким образом, чтобы от соседних зон Френеля разность хода волн до данной точки составляла половину длины волны ( ).
5. Пусть свет падает
на экран с отверстием радиусом
.
Число зон
Френеля,
укладываемых на отверстии, в случае
сферических волн i=
,
где R
– радиус волновой поверхности (расстояние
от источника до экрана с отверстием),
r0
– расстояние от отверстия до экрана,
на который падает свет после прохождения
отверстия.
В случае плоской
волны (R=
)
число зон i=
6. Условие max, если число зон i нечетное, если число зон i четное, условие min.
Радиус i-й
зоны Френеля
=
7. В случае дифракции
на одной щели
шириной а
для плоских волн: аSin
=(2
)
,
=1,
2, …- условие max
аSin =2 , =1, 2, ... – условие min
При =0 выполняется условие max
8. Для дифракционной решетки с d=a+b
условие max:
dSin
=
,
=0,
1, 2, ...
условие min: aSin =m , m=1, 2, ...
- № 20, 94, 119, 169, 194, 218, 244, 254, 290, 328, 368, 378, 504