18.Веса функций измеренных величин.
Если известны веса аргументов функции то можно найти вес самой функции.
Можно
вывести формулу по которой определяется
веса. При k=1
откуда
– обратный вес.
19.Средняя квадратическая погрешность единицы веса.
При
оценке точности неравноточных измерений
в качестве дисперсии принимают дисперсию
измерений
вес которой равен 1, т.к.
неизвестно но ее заменяют с средней
погрешностью
.
Ради кратности ее называют средним квадратической погрешностью единицы веса.
;
;
20.Математическая обработка результатов неравноточных измерений.
Допустим
имеется n
групп равноточных измерении, при этом
число измерений в каждой группе равно
.
По каждой группе
Математическая обработка ряда результатов прямых неравноточных измерений одной величины выполняется в следующей последовательности.
1. Вычисление весового среднего (общей арифметической средины)
.
По
этой формуле определяется среднее
весовое в том случае когда
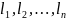получены из некоторой изм. весами
.
Для упрощения вычислении используются
приближенное значение
(выбирается
как при вычис. сред.)
– средне весовое
с приб. значением.
Вычисление средней квадратической погрешности одного измерения по уклонениям от арифметической средины, используя формулу Бесселя для неравноточных измерений:
.
Вычисление средней квадратической погрешности весового среднего
.