19) Закон Ома для участка цепи и в дифференциальной форме. Сопротивление проводника. Вычисление сопротивления. Последовательное и параллельное соединение сопротивления

- закон Ома.

Последовательное: I1=I2=I3; R=R1+R2+R3;

Параллельное: U1=U2=U3; I=I1+I2+I3; 1/R=1/R1+1/R2.

20)Электродвижущая сила (э.Д.С). Закон Ома для полной цепи. Закон Джоуля-Ленца.

Физическая величина, равная отношению работы Aст сторонних сил при перемещении заряда q от отрицательного полюса источника тока к положительному к величине этого заряда, называется электродвижущей силой источника (ЭДС):

- Эта формула выразит закон Ома для полной цепи: сила тока в полной цепи равна электродвижущей силе источника, деленной на сумму сопротивлений однородного и неоднородного участков цепи.

Закон Джоуля-Ленца - количество теплоты, которое выделяется в проводнике с током, пропорционально квадрату силы тока, времени его прохождения и сопротивлению проводника. .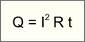

21) Расчёт цепей постоянного тока. Правила Кирхгофа. Пример.

Первое правило Кирхгофа: алгебраическая сумма сил токов для каждого узла в разветвленной цепи равна нулю: I1+I2+I3+…In=0

Второе правило Кирхгофа можно сформулировать так: алгебраическая сумма произведений сопротивления каждого из участков любого замкнутого контура разветвленной цепи постоянного тока на силу тока на этом участке равна алгебраической сумме ЭДС вдоль этого контура.

Первое и второе правила Кирхгофа, записанные для всех независимых узлов и контуров разветвленной цепи, дают в совокупности необходимое и достаточное число алгебраических уравнений для расчета значений напряжений и сил токов в электрической цепи. Для цепи, изображенной на рис. 1.10.2, система уравнений для определения трех неизвестных токов I1, I2 и I3 имеет вид:

I1R1 + I2R2 = – E1 –E 2,

– I2R2 + I3R3 =E 2 + E3,

– I1 + I2 + I3 = 0.

22) Взаимодействие линейных токов. Полевая трактовка взаимодействия токов. Единица силы тока – Ампер.

Закон взаимодействия линейных токов: "Два параллельных и одинаково направленных тока взаимно прибиваются, между тем как два параллельных и противоположно направленных тока взаимно отталкиваются".

Полевая трактовка взаимодействия токов:

1) Элемент тока I1dI1 создает в точке нахождения элемента тока I2dI2 магнитное поле с индукцией. dB12=(M0*/3.14*4)*((I1dI1*r12)/r12^3).

2) на элемент тока I2dI2, находящейся в точке с магнитной индукцией dB12,действует сила: dF12=I2dI2*dB12.

23)Сила Ампера. Сила, действующая на движущуюся заряженную частицу в магнитном поле (сила Лоренца).

Сила Ампера это та сила, с которой магнитное поле действует на проводник, с током помещённый в это поле. Величину этой силы можно определить с помощью закона Ампера. В этом законе определяется бесконечно малая сила для бесконечно малого участка проводника. Что дает возможность применять этот закон для проводников различной формы. .

Направление силы Ампера находится по правилу левой руки. Формулировка этого правела, звучит так. Когда левая рука расположена таким образом, что лини магнитной индукции внешнего поля входят в ладонь, а четыре вытянутых пальца указывают направление движения тока в проводнике, при этом отогнутый под прямым углом большой палец будет указывать направление силы, которая действует на элемент проводника.

Некоторые проблемы возникают, при использовании правела левой руки, в случае если угол между индукцией поля и током маленький. Трудно определить, где должна находиться открытая ладонь. Поэтому для простоты применения этого правела, можно ладонь располагать так, чтобы в нее входил не сам вектор магнитной индукции, а его модуль.

Из закона Ампера следует, что сила Ампера будет равна нулю, если угол между линией магнитной индукции поля и током будет равен нулю. То есть проводник будет располагаться вдоль такой линии. И сила Ампера будет иметь максимально возможное значение для этой системы, если угол будут составлять 90 градусов. То есть ток будет перпендикулярен линии магнитной индукции.

С помощью закона Ампера можно найти силу, действующую в системе из двух проводников. Представим себе два бесконечно длинных проводника, которые находятся на расстоянии друг от друга. По этим проводникам протекают токи. Силу, действующую со стороны поля создаваемого проводником с током номер один на проводник номер два можно представить в виде: .

FЛ = q υ B sin α – сила Лоренца. При движении заряженной частицы в магнитном поле сила Лоренца работы не совершает.