Интерпретация моделей авторегрессии.

Обратимся к модели авторегрессии. Пусть имеется следующая модель: yt=a+b0*x1+c1*yt-1+ εt. Как и в модели с распределенным лагом, b0 в этой модели характеризует краткосрочное изменение yt под воздействием изменения xt на 1 ед. Однако промежуточные и долгосрочный мультипликаторы в моделях авторегрессии несколько иные. К моменту времени (t+1) результат yt изменился под воздействием изменения изучаемого фактора в момент времени t на b0 ед., а yt+1 под воздействием своего изменения в непосредственно предшествующий момент времени – на c1 ед.. Таким образом, общее абсолютное изменение результата составит b0c1 ед.. Аналогично в момент времени (t+2) абсолютное изменение результата составит b0c12 ед. и т.д.. Следовательно, долгосрочный мультипликатор в модели авторегрессии можно рассчитать как сумму краткосрочного и промежуточных мультипликаторов: b=b0+b0c1+b0c12+b0c13+…

Учитывая, что практически во все модели авторегрессии вводится так называемое условие стабильности, состоящее в том, что коэффициент регрессии при переменной yt-1 по абсолютной величине меньше единицы (|c1|<1), соотношение можно преобразить следующим образом: b=b0*(1+c1+c12+c13+…)= b0/(1- c1), где |c1|<1.

Отметим, что такая интерпретация коэффициентов модели авторегрессии и расчет долгосрочного мультипликатора основаны на предпосылке о наличии бесконечного лага в воздействии текущего значения зависимой переменной на ее будущие значения.

Основные этапы моделирования связи методом регрессии и корреляции.

спецификация модели (выбор функции)

теснота связи. Линейный коэффициент корреляции

оценка критерия уравнения и параметра. Критерии Фишера и Стьюдента.

Прогнозирование

Спецификация моделей парной регрессии.

Парная регрессия представляет собой модель вида y=f(x). В каждом отдельном случае yi=y¯xi +Ei, где

yi – значение результативного признака; y¯xi – теоретическое значение результативного признака; Ei – СВ или возмущение.

Ei зависит:

от ошибок спецификации

неправильный выбор математической функции

недоучет в уравнении регрессии какого-либо существенного фактора

от ошибок выборки. Возникает в силу неоднородности данных и уравнение регрессии, построенное с учетом аномальных наблюдений, не имеет смысла.

от ошибок измерения. На ошибки измерения исследователь влиять не может

В эконометрическом исследовании используются следующие типы функций:

линейная

парабола 2 и 3 порядка

гипербола

степенная

показательная

Выбор вида математической функции осуществляется 3 методами:

графический

аналитический

экспериментальный

Линейная регрессия и корреляция

Линейная функция имеет вид yx=a +bx

A,b – параметры уравнения, которые находятся МНК, решением системы нормальных уравнений: b – является коэффициентом регрессии, показывающим

насколько в среднем изменяется результат с изменением фактора на 1.

A – значение y в точке x=0. если а >0, то относительное изменение результата происходит медленнее, чем изменение фактора.

Уравнение регрессии всегда дополняется показателем тесноты связи. Для линейной функции – линейный коэффициент корреляции.

r< 0 – обратная связь r> 0 – прямая связь r=0 – связь отсутствует r> +- 0,7 – связь тесная

r2 – линейный коэффициент детерминации, характеризует долю дисперсии результативного признака, объясняемую регрессией в общей дисперсии результативного признака.

Нелинейная регрессия

Различают 2 класса нелинейных регрессий:

регрессии нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам. К этому классу относятся параболы различных порядков и равносторонняя гипербола. Оценки параметров данной функции даются с помощью МНК.

Yx = a+bx+cx2

na+b∑x+c∑ x2 = ∑y

a∑x+b∑ x2 +c∑ x3 =∑yx

a∑ x2 +b∑ x3 +c∑ x4 =∑yx2

Yx = a+b*1/x

n*a+b∑1/x = ∑y

a∑1/x+b∑(1/x)2 = ∑(y*1/x)

регрессии нелинейные по оцениваемым параметрам:

нелинейные модели. Внутренне нелинейные. Логистическая, обратная. к ним МНК не применим, а данные функции невозможно привести к линейному виду путем логарифмирования.

нелинейные модели. Внутренне линейные относятся показательная, степенная и экспоненциальная функции. Для оценки параметров этих функций МНК не применим, а значения параметров находятся путем логарифмирования и приведения к линейному виду. Обратный переход от линейной функции к степенной осуществляется с помощью потенцирования….. уравнения нелинейной регрессии так же дополняются показателями тесноты связи – индекс корреляции. Чем ближе к 1, тем теснее связь между показателями. R2 – индекс детерминации и чаще используется для выбора той или иной нелинейной модели. Оценка надежности уравнения нелинейной регрессии осуществляется с помощью f-критерия Фишера. M – число параметров при переменных х.

Fтабл. Определяется с учетом α и числом степеней свободы V1=m v2=n-m-1. Fрасч>Fтабл – уравнение признается значимым. R2 используется для обоснования возможности применения линейной функции. Если величина….., то предположение о линейной форме связи считается оправданным. Если…., то проводится оценка существенности различий через t-критерий Стьюдента.

Tрасч сравнивается с Tтабл, α=0,05, V=n-m(m-число параметров уравнения).

Tрасч>tтабл – различия между рассматриваемыми показателями корреляции существенны и замена нелинейной регрессии уравнением линейной функции невозможна.

Коэффициент эластичности для математических функций

Чтобы иметь представление о качестве модели определяется ошибка аппроксимации. Критерием выбора является min ошибки, а средняя ошибка <=10%

Прогнозирование по линейному уравнению регрессии.

Прогноз может осуществляется точечной и интервальной оценкой. В Уравнение регрессии подставляется предсказываемое значение факторного признака.

Интервальная оценка, этапы:

определяется интегральная ошибка прогноза

предельная ошибка прогноза с учетом определенной вероятности

фактическая реализация прогноза находится в пределах

Относительная величина различий значений верхней и нижней границ прогноза находится по формуле, характеризует точность прогноза:

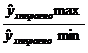
D = ; D≤2; D=1.2-1.3 – точный прогноз