7. Примеры решения задач

№1. Определить состояние водяного пара, если давление его p = 0,6 МПа, а удельный объем v = 0,3 м³/кг.

Решение

Давлению 0,6 МПа должен соответствовать удельный объем сухого насыщенного пара v″ = 0,3156 м³/кг. Так как для заданного состояния v″ > v, то пар является влажным. Степень сухости его из уравнения для V_x

,

или по приближенной формуле

.

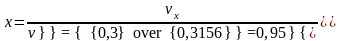Таким образом, расчет по приближенной формуле для данного случая весьма точен.

№2. Определить внутреннюю энергию сухого насыщенного пара при p=1,5МПа.

Решение

Для сухого насыщенного пара

.

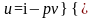По таблице насышенного водяного пара (вход по давлению):

;

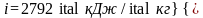Следовательно,

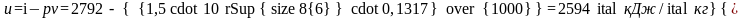
№3. Определить энтальпию и внутреннюю энергию влажного насыщенного пара при p=1,3МПа и степени сухости пара x=0,98.

Решение

Для влажного насыщенного пара

По таблицам насыщенного водяного пара (вход по давлению) находим

i′=814,5кДж/кг; r=1973кДж/кг;

v″=0,1512м³/кг,

отсюда

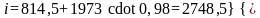кДж/кг

Удельный объем влажного пара определяется по приближенной формуле:

.

Из формулы для i_x влажного насыщенного пара имеем

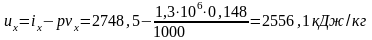
№4. Найти энтропию влажного насыщенного пара p = 2,4 МПа и x = 0,8.

Решение

Для влажного насыщенного пара

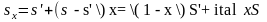
По таблице насыщенного водяного пара (вход по давлению) находим

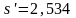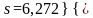кДж/( К×кг); кДж/(К×кг),

отсюда

.

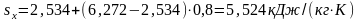№5. Найти массу, внутреннюю энергию, энтальпию и энтропию 6 м³ насыщенного водяного пара при давлении p = 1,2 МПа и сухости пара x =0,9.

Решение

Удельный объем влажного насыщенного пара по приближенной формуле

v_x=x v²_x = 0,1633×0,9 = 0,147 м³/кг.

Масса пара

.

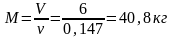Внутренняя энергия пара

.

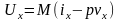Энтальпия пара

.

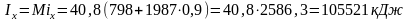Следовательно,

.

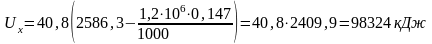Энтропия пара

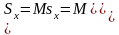
№6. Водяной пар имеет параметры

, .

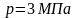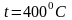Определить значения остальных параметров.

Решение

Так как температура пара больше критической, то пар приприведенных параметров перегретый. По таблице перегретого пара находим

; ;

.

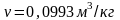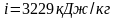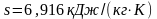Плотность пара

.

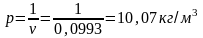Внутреннюю энергию пара определяем из общей зависимости

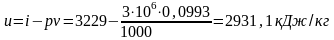
№7. Определить количество теплоты, затрачиваемой на перегрев 1кг сухого насыщенного пара при 9 МПа до 500°С.

Решение

Из таблицы насыщенного водяного пара (вход по давлению) находим

; .

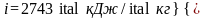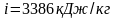Следовательно, теплота изобарного перегрева пара

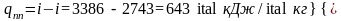
№8. В паровом котле объемом V=12м³ находится 1800 кг воды и пара при давлении 11 МПа и температуре насыщения.

Определить массы воды и сухого насыщенного пара, находящиеся в котле.

Решение

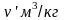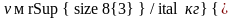Обозначим массы воды и пара соответственно через М_в и М_п (в кг). Удельный объем кипящей воды равен , а удельный объем сухого насыщенного пара - . Следовательно, объем, занимаемый водой,

,

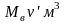а объем, занимаемый паром,

,

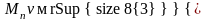суммарный объем

.

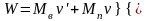Но так как

,

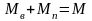То

.

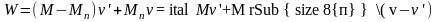Из этого выражения

.

Из таблице насыщенного водяного пара получаем

.

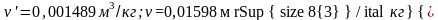Следовательно, масса пара

,

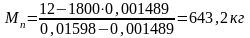а масса воды

.

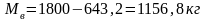Задача может быть решена и другим путем. Если в паровом котле при рассматриваемых условиях находилась бы только вода, то ее масса

.

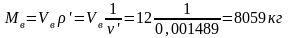В действительности масса воды меньше на

,

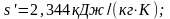так как плотность воды при давлении 11 МПа больше плотности пара при том же давлении на

.

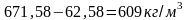
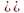Следовательно, объем пара в котле

,

а его масса

.

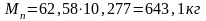Вода занимает объем

,

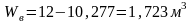следовательно, ее масса

.

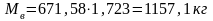№9. Задано состояние пара:

p=1,6МПа; x=0,96.

Определить остальные параметры, пользуясь диаграммой, и сравнить их со значениями этих же параметров, вычисленных с помощью таблиц водяного пара и соответствующих формул.

Решение

На диаграмме is находим точку С_x, характеризующую данное состояние. Проектируя ее соответственно на ось ординат и ось абсцисс, находим значения i_x =2716кДж/кг и s_x=6,26кДж/(кг×К). Величина удельного объема пара определяются по значению изохоры, проходящей через точк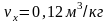 . Для определения температуры пара нужно от точки C_x подняться по изобаре 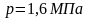до верхней пограничной кривой (точка C²). Через эту точку проходит изотерма 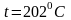; эта температура и является температурой насыщенного пара при давлении 1,6 МПа.

Сопоставим полученные значения со значениями этих же параметров, вычисленных при помощи таблиц водяного пара и соответствующих формул.

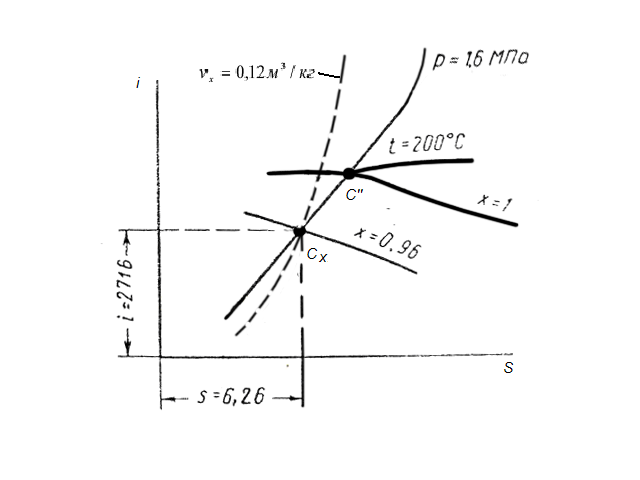
По таблице насыщенного водяного пара (вход по давлению) для пара при давлении 1,6МПа находим

; ;

; ;

.

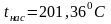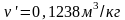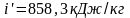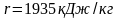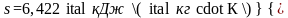Энтальпию пара определяем по формуле (187):

.

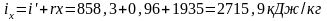Энтропию влажного насыщенного пара вычисляем по формуле:

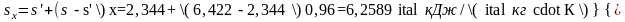
Значение удельного объема находим по приближенной формуле:

.

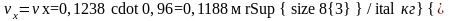Как видно, совпадение значений параметров вполне удовлетворительное.

№10 В закрытом сосуде содержится 1м³ сухого насыщенного пара при давлении 1 МПа. Определить давление, степень сухости пара и количество отданной им теплоты, если он охладился до 60 °С.

Решение

Пользуясь таблицами насыщенного водяного пара (по температуре) получаем при t₂=60 °С давление пара p=0,019917 МПа.

Так как процесс происходит при постоянном объеме, то с помощью таблиц насыщенного водяного пара (вход по давлению) при p=1,0МПа находим:

.

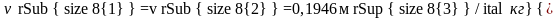По уравнению , откуда

.

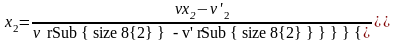Пользуясь таблицей насыщенного водяного пара (вход по температуре), находим при t₂=60°С

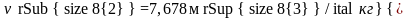и

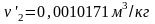
И таким образом

.

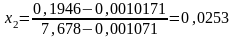Количество теплоты в изохорном процессе вычисляется по формуле .

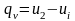Определяем значения внутренней энергии пара в начале и в конце процесса:

.

Значение i₂ находим по формуле (187):

,

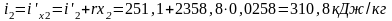Следовательно,

Таким образом,

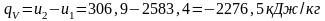
Так как в рассматриваемом процессе участвует 1м³ пара и плотность его по таблице насыщенного водяного пара (вход по давлению) при p=1 МПа r²=5,139 кг/м³ , то

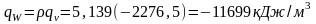
№11. В паровом котле находится 8250 кг пароводяной смеси с паросодержанием x=0,0015 при давлении 0,4 МПа.

Сколько времени необходимо для поднятия давления до 1 МПа при закрытых вентилях, если пароводяной смеси сообщается 18 МДж/мин?

Решение

Удельный объем пароводяной смеси в начальном состоянии:

.

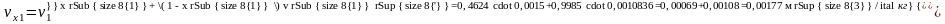Конечно содержание пара определяется из условия задачи:

v₂=v_x1

При давлении P₂=1,0МПа по таблицам насыщенного водяного пара

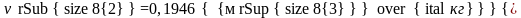
Т.к. v_2²>v₂ ,то в конечном состоянии пар является влажным насыщенным, т.е. v₂=v_x2 , и тогда:

.

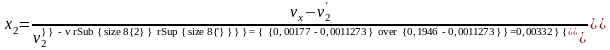Так как изменения состояния пароводяной смеси происходит при постоянно объеме, то количество теплоты, необходимой для поднятия давления до 1 МПа, по уравнению (201) составит

.

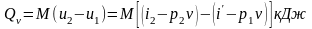Определяем энтальпию пара в начальном и конечном состояниях:

;

.

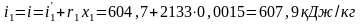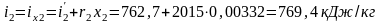Следовательно,

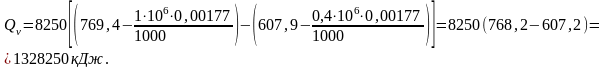
Время, необходимое для поднятия давления до 1 МПа при закрытых вентилях, составляет

№12. Влажный пар имеет при давлении p=1,5 МПа паросодержание x=0,80.

Какое количество теплоты нужно сообщить 1 кг данного пара, чтобы довести его степень сухости при постоянном давлении до x₂=0,95.

Решение

Количество теплоты в изобарном процессе

.

Для рассматриваемого случая

;

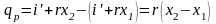Значения i¢ и r берутся из таблиц насыщенного водяного пара (вход по давлению).

.

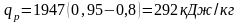№13. 1 кг водяного пара при p = 1 МПа и t₁ = 240°С нагревается при постоянном давлении до 320°С.

Определить затраченное количество теплоты, работу расширения и изменение внутренней энергии пара.

Решение

Количество теплоты изобарном процессе

.

По таблице насыщенного водяного пара (вход по давлению) определяем t_нас для p=1,0МПа.

Так как при p = 1 МПа температура насыщения t_н = 179,88°С, то пар в исходном и конечном состояниях перегретый. Пользуясь таблицами перегретого пара, получаем

.

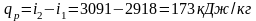Работа расширения определяется по формуле

,

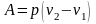или, пользуясь табл. XV,

.

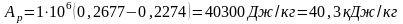Изменение внутренней энергии проще всего определяется из уравнения первого закона термодинамики:

.

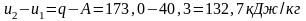№14. Энтальпия влажного насыщенного пара при давлении p_i = 1,4 МПа составляет i_x = 2705 кДж/кг.

Как изменится степень сухости пара, если к 1 кг его будет подведено 40 кДж теплоты при постоянном давлении?

Решение

Определяем начальную степень сухости пара из равенства:

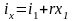
Из таблиц насыщенного водяного пара при p = 1,4 МПа:

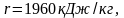
следовательно,

.

Конечную степень сухости пара определяем из равенства:

,

из этого получаем

.

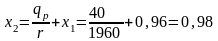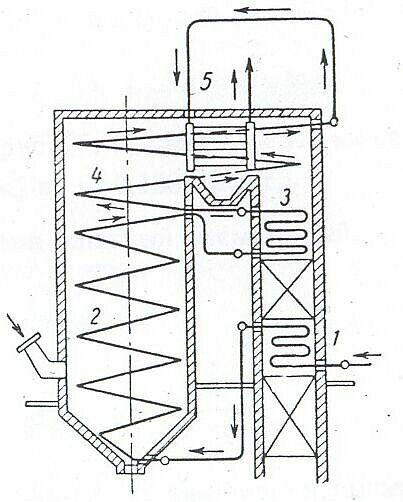
№15. Из парового котла поступает в пароперегреватель 2700 кг/ч пара при p=1,6 МПа и х=0,98. Температура пара после пароперегревателя равна

400°С.

Найти количество теплоты, которое пар получает в пароперегревателе при изобарном пароперегреве, и отношение диаметров паропроводов до и после пароперегревателя, считая скорости пара в них одинаковыми.

Решение

Количество теплоты, которое нужно затратить для превращения 1 кг пара заданных начальных параметров в перегретый пар,

.

В нашем случае q_р=i₂-i_x1, где i_x1=i¢₁+r₁x

Пользуясь таблицами насыщенного и перегретого пара, находим

.

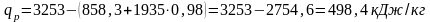Общее количество теплоты

.

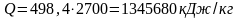Определяем значения удельного объема пара до (v₁ ) и после (v₂ ) пароперегревателя:

.

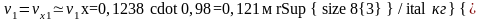Пользуясь таблицами перегретого пара, получаем

.

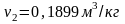Как известно, уравнение неразрывности для установившегося течения жидкости или газа имеет вид:

.

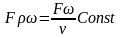Обозначая сечения трубопровода до и после пароперегревателя соответственно через F₁ и F₂ и скорость протекания пара в них через ω, получаем

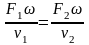
или

,

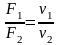а также

.

№16. От 1кг водяного пара с начальными параметрами p_i=1,6МПа и v₁=0,15м³/кг отводится теплота при p=const. При этом в одном случае конечный объем v₂=0,13 м³/кг, а в другом - v₂=0,10 м³/кг.

Определить конечные параметры, количество теплоты, участвующей в процессе, работу и изменение внутренней энергии.

Р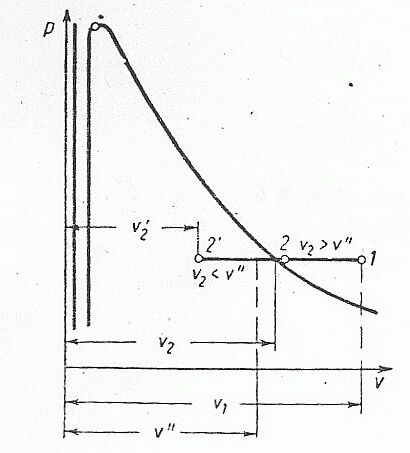 ешение

Первый случай.

Определяем состояние пара. По таблице насыщенного водяного пара для p=1,6 МПа находим v₁″=0,1238м³ /кг.

Так как v₁>v²₁, то пар в начальном состоянии перегретый.

Для конечного состояния имеем v₂=0,13м³/кг; v₂″=0,1238м³/кг, т.е. v₂>v²₂ , следовательно, пар остается перегретым.

Определяем начальную и конечную температуру пара. По табл. перегретого пара, интерполируя между v=0,1452м³/кг и v=0,1519м³/кг, p=1,6 МПа, t=280°С находим t₁=274°С.Конечная температура перегретого пара для v₂=0,13м³/кг и p=1,6МПа равна t₂=218°С.

Количество теплоты в процессе

.

По таблицам перегретого пара

; ,

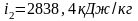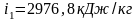Следовательно,

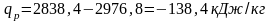
Работа пара в изобарном:

.

Изменение внутренней энергии находим из уравнения первого закона термодинамики:

.

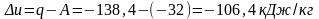Второй случай. Так как

,

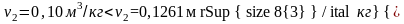то пар в конечном состоянии влажный насыщенный, т.с. v₂=v_x2

Определяем степень сухости пара

,

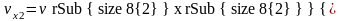Откуда

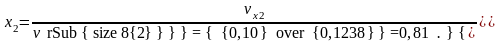
Температуру пара определяем по таблицам насыщенного пара для давления : t₂₌t_нас2

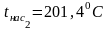
Количество теплоты в процессе

.

Пользуясь таблицами насыщенного водяного пара получаем

.

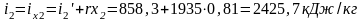Таким образом,

.

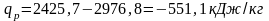Работа пара в изобарном процессе

.

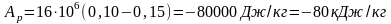Изменение внутренней энергии

.

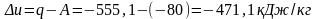№17. 2 кг пара, занимающие при p=0,8 МПа объем V=0,15 м³, изотермически расширяются до V₂=0,35 м³.

Определить работу расширения, количество подведенной теплоты и степень сухости пара.

Решение

Определяем удельный объем пара:

;

.

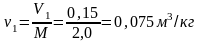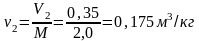По таблицам насыщенного водяного пара находим при p=0,8 МПа удельный объем .

Так как v₁ меньше v₁″, то пар в начальном состоянии влажный насыщенный. Рассматриваемый изотермический процесс, протекающий в области влажного насыщенного пара, одновременно является процессом изобарным, следовательно v₁′=v₂′, v₁″=v₂″, i₁′=i₂′, S₁′=S₂′ и S₁″=S₂″. Т.к. v₂<v₂″, то пар в конечном состоянии также является влажным насыщенным. Степень сухости в начальном и конечном состояниях:

;

.

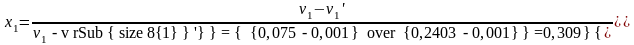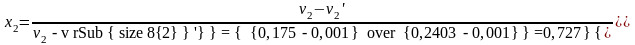Работа расширения и количество подведенной теплоты в нашем случае определяются по формулам изобарного процесса:

. .

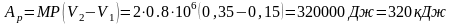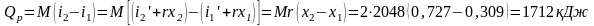Количество подведенной теплоты может быть также определено по формуле изотермического процесса:

,

где Т=Т_нас в К при данном давлении P=0,8 МПа;

s₁ и s₂ – энтропия влажного насыщения пара в начальном и конечном состояниях, определяемая по уравнениям.

;

;

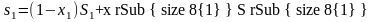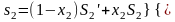Т.к. S₁′=S₂′=S′ и S₁″=S₂″=S″, то

,

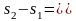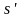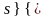где и - энтропии кипящей воды и сухого насыщенного пара при данном давлении Р=0,8 МПа.

Таким образом,

.

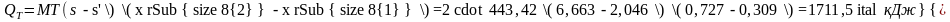I-S диаграмма водяного пара