Более строгое представление о нечётких множествах (нм)

Пусть Е - универсальное или несущее множество, х – элемент Е, R - некоторое свойство, тогда нечёткое подмножество А несущего множества Е, элементы которого удовлетворяют свойству R, определяется как множество упорядоченных пар.

А={μ_A(x)/x}, где μ_A(x) – характеристическая функция принимающая значение 1 в том случае, если х полностью удовлетворяет свойству R и значениям от 0 до 1, если х не полностью удовлетворяет свойству R и 0, если х вообще не удовлетворяет свойству R.

Множество М называется множеством принадлежности, если М=[0..1], то А нечёткое множество, если М={0,1}, то А чёткое множество. Функция принадлежности указывает степень (или уровень) принадлежности элемента множеству А.

Пример записи НМ.

Если Е состоит Е={x₁,x₂,x₃,x₄,x₅}М=[0,1], A – нечёткое множество для которого μ_A(x₁)=0,3 , μ_A(x₂)=0 , μ_A(x₃)=1 , μ_A(x₄)=0,6 , μ_A(x₁)=0,9. тогда множество А можно представить в виде:

А={0,3/x₁; 0/x₂; 1/x₃; 0,6/x₄; 0,9/x₅;}

Рассмотрим пример, когда универсальным множеством Е является множество машин.

Е={запорожец; жигули; мерседес; БМВ; феррари}

На основе универсального множества создаётся НМ А.

А=”машина для бедных” . Т.о. функция принадлежности для данного множества может выглядеть следующим образом:

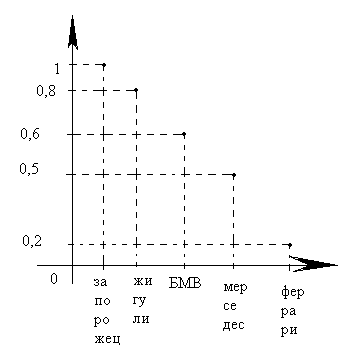
Точно также можно построить на основе этого множества НМ «престижные», «среднего класса», «скоростные» и т.д.

В рассмотренных примерах использованы прямые методы, когда эксперт либо просто задаёт для каждого х€Е значение μ_A(x), либо определяет функции совместимости. При прямых методах используются также групповые прямые методы:

Например: Группе экспертов предъявляют конкретное лицо и каждый должен дать один из двух ответов – «человек лысый» или «не лысый». Тогда количество утвердительных ответов делённое на общее число экспертов даёт значение μ_лысый данного лица.

С НМ можно выполнять те же действия, что и с числовыми множествами но они достаточно сложнее выполняются.

Например: построить характеристическую функцию для множества А- множество детей в 11а классе способных к математике. В- множество детей в 11а классе способных к музыке. Изобразить сначала отдельно две характеристические функции для множества А (5 детей), В (4), затем построить пересечение этих двух множеств.

μ(х)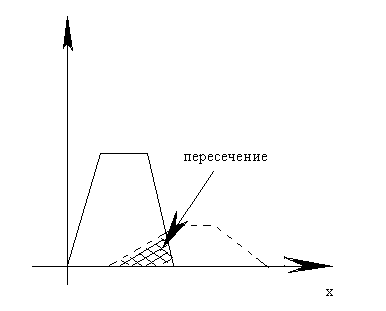

Пусть А и В НМ на универсальном множестве Е, говорят, что А содержится в В, если для любого х из Е μ_А(x)≤ μ_B(x) и обозначают А B.

Пример: А-множество чисел очень близких к 10, В-множество чисел близких к 10, тогда можно сказать, что А B.

Пересечением НМ А и В называется наибольшее нечёткое подмножество содержащееся одновременно в А и в В.

μ_{А B}(x)=min(μ_А(x), μ_B(x))

Объединением НМ А и В называется НМ обозначаемое А В, функция принадлежности которого определяется следующим образом:

μ_{A B}(x)=max(μ_А(x), μ_B(x)).

Моделирование в среде MathCad, Maple

Для того, чтобы решить простейшее уравнение в среде MathCAD задаётся уравнение F(x)=0,затем выписываются отдельно коэффициенты этого уравнения.

тогда задаём x (1,-5.6) промежуток где лежит корень уравнения а затем вызывается функция А:=polyroots(x).

Для того, чтобы решить уравнение в среде Maple используют следующие функции:

Solve(f(x),x);

F(x) это уравнение, х – переменная,

или fsolse(f(x),x,p);

p-параметр, p=[-1,1], после каждой скобки знак ;

Замечание. Если необходимо решить уравнение в символьном виде, то для него используется функция solve(eq,var);

Eq- уравнение, var –переменная.

Для того чтобы, изобразить график в среде MathCAD, надо сначала указать диапазон изменения аргумента т.е. показать как меняется х и у.

x:=-5,-4.5..5

y:=-10,-9.5..10 нажав клавиши . . - :

Затем вызывается из меню график и задаётся на графике х и f(x).

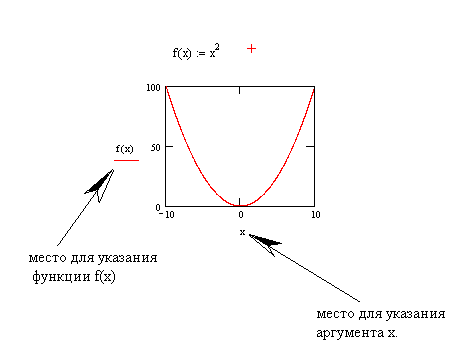
Для задания поверхности надо указать диапазоны, указать формулу, затем в меню «графики» вызываем «поверхность».

Все графики необходимо располагать строго после описания диапазонов и функций.

Maple позволяет решать уравнения и изображать графики функций.

Для построения графика указывается значение переменной (имя)

P:=plot(<функция 1>,<функция 2>,<диапазон для аргумента>): p;

Пример:

P;=plot(x³,x-1,x:=-2..2):p; - это пример решения уравнения x³-x-1.

Для моделирования в среде Maple можно использовать построение графиков а также построение поверхностей.