Смешанное соединение проводников

Смешанное соединение проводников — это такое соединение, при котором некоторые проводники соеденины последовательно, а некоторые — параллельно:

Чтобы найти силу тока, напряжение и сопротивление при смешанном соединении, нужно разбить его на простые участки, и найти силу тока, напряжение и сопротивление в них по вышеприведённым правилам, при этом схема упростится и найти в ней необходимые параметры не составит труда:

Чтобы разобраться в некоторых схемах, их проще заменить на эквивалентные:

Правила Кирхгофа сформулированы немецким физиком Густавом Робертом Кирхгофом.

Первое правило Кирхгофа алгебраическая сумма токов, сходящихся в узле, равна нулю.

Первое правило Кирхгофа является следствием закона сохранения заряда, согласно которому ни в одной точке проводника не должны накапливаться или исчезать заряды.

Первое правило Кирхгофа можно сформулировать и так: количество зарядов, приходящих в данную точку проводника за некоторое время, равно количеству зарядов, уходящих из данной точки за то же время.

Второе правило Кирхгофа является обобщением закона Ома. Второе правило Кирхгофа - в любом замкнутом контуре разветвленной цепи алгебраическая сумма ЭДС равна алгебраической сумме произведений токов на сопротивления соответствующих участков этого контура:

Правила Кирхгофа позволяют определить силу и направление тока в любой части разветвленной цепи, если известны сопротивления ее участков и включенные в них ЭДС.

Билет 24

Термоэлектронная эмиссия

Термоэлектронная эмиссия, Ричардсона эффект, испускание электронов нагретыми телами (твёрдыми, реже — жидкостями) в вакуум или в различные среды. Впервые исследована О. У.Ричардсоном в 1900— 1901. Т. э. можно рассматривать как процесс испарения электронов в результате их теплового возбуждения. Для выхода за пределы тела (эмиттера) электронам нужно преодолеть потенциальный барьер у границы тела; при низких температурах тела количество электронов, обладающих достаточной для этого энергией, мало; с увеличением температуры их число растет и Т. э. возрастает (см. Твёрдое тело).

Главной характеристикой тел по отношению к Т. э. является величина плотности термоэлектронного тока насыщения j_o при заданной температуре. При Т. э. в вакуум однородных (по отношению к работе выхода) эмиттеров в отсутствии внешних электрических полей величина j₀ определяется формулой Ричардсона — Дэшмана:

 .    (1)

Здесь А — постоянная эмиттера (для металлов в модели свободных электронов Зоммерфельда: А = А₀ = 4pek²m/h³ = 120,4 а/К²см², где е — заряд электрона, m — его масса, k — Больцмана постоянная, h — Планка постоянная), Т — температура эмиттера в К,    — средний для термоэлектронов разных энергий коэффициент отражения от потенциального барьера на границе эмиттера; ej — работа выхода. Испускаемые электроны имеют Максвелла распределение начальных скоростей, соответствующее температуре эмиттера.

Билет 25

Элементарная классическая теория проводимости металлов: обоснование законов Ома, Джоуля-Ленца

Некоторые важные свойства свободных электронов в металлах непосредственно связаны с их поведением, которое эффективно объясняется методами статистической физики. Классическая теория свободных электронов Джоуля-Лоренца, созданная в начале ХІХ столетия, выходила из предположения, что электронный газ в металлах можно рассматривать как почти идеальный газ. К основным положениям упомянутой теории относятся следующие утверждения:

- считается, что каждый атом отдает в "общее пользование" не меньше одного электрона.

Элементарная классическая теория и свободные электроны считаются такими, которые не взаимодействуют ни с ионами решетки, ни между собой (в действительности два этих взаимодействия лишь частично компенсируют одна другую).

- считается, что в интервалах между столкновениями (коллизиями) каждый свободный электрон двигается прямолинейно и равномерно, если отсутствует внешнее электромагнитное поле. Во внешних силовых полях свободные электроны двигаются за законами Ньютона.

- столкновения электронов с ионами решетки имеют место, а столкновение электронов между собой не учитываются

- вероятность столкновения для свободного электрону за единицу времени равняется, где - среднее время свободного пробега, или иначе время релаксации.

Исходя из следующих предположений, рассмотрим поведение газа свободных электронов во внешнем электрическом поле напряженности. На каждый электрон действует сила, которая предоставляет емуускорение. Модуль средней скорости, которую получают электроны от поля. равняется половине максимальной, если считать, что начальная скорость электрона (скорость после столкновения) является нулевой.

Это, что проводимость металлов заметно падает с температурой. Экспериментально чаще изучают температурную зависимость удельного сопротивления. В области высоких температур удельное сопротивление растет с температурой линейно, однако, в небольшой области ближе к температуре абсолютного нуля, он перестает зависеть от температуры. В этой области удельное сопротивление (окончательное сопротивление) определяется примесями и дефектами кристаллов.  Элементарная классическая теория, одним из недостатков теории газа свободных электронов Друде-Лоренца есть неспособность объяснить зависимость. Вместо линейной зависимости, эта теория дает зависимость типу, который не отвечает экспериментальным данным. Исходя из постулатов теории Друде-Лоренца можно получить также и закон Джоуля-Ленца.

Билет 26

Формулировка закона Ома

Сила тока в участке цепи прямо пропорциональна напряжению на концах этого проводника и обратно пропорциональна его сопротивлению: I = U / R; [A = В / Ом]

Ом установил, что сопротивление прямо пропорционально длине проводника и обратно пропорционально площади его поперечного сечения и зависит от вещества проводника. R = ρl / S, где ρ - удельное сопротивление, l - длина проводника, S - площадь поперечного сечения проводника.

Закон Джоуля — Ленца. К концу свободного пробега электрон под действием поля приобретает дополнительную кинетическую энергию

                                         (103.3)

При соударении электрона с ионом эта энергия полностью передается решетке и идет на увеличение внутренней энергии металла, т. е. на его нагревание.

За единицу времени электрон испытывает с узлами решетки в среднем z столкновений:

                                                (103.4)

Если n — концентрация электронов, то в единицу времени происходит пz столкновений и решетке передается энергия

                                                         (103.5)

которая идет на нагревание проводника. Подставив (103.3) и (103.4) в (103.5), получим таким образом энергию, передаваемую решетке в единице объема проводника за единицу времени,

                                                (103.6)

Величина w является удельной тепловой мощностью тока. Коэффициент пропорциональности между w и E² по (103.2) есть удельная проводимость ; следовате­льно, выражение (103.6)—закон Джоуля—Ленца в дифференциальной форме (ср. с (99.7)).

Билет 27

Взаимодействие движущихся зарядов и токов Известно, что взаимодействие неподвижных зарядов описывается законом Кулона. Возникает вопрос,  будут ли наблюдаться какие либо особенности при взаимодействии зарядов движущихся? Используя выводы специальной теории относительности и закон сохранения заряда можно показать, что взаимодействие движущихся зарядов осуществляется не только кулоновской силой, но также и силой другого типа, называемой магнитной. В случае движения зарядов с нерелятивистскими скоростями их магнитное взаимодействие много меньше кулоновского, поэтому экспериментально выделить магнитное взаимодействие на фоне электрического для дискретных зарядов очень сложно. Электрическое и магнитное взаимодействия неразрывно связаны между собой и образуют электромагнитное взаимодействие. При специальном выборе системы отсчета сила взаимодействия зарядов может оказаться или чисто электрической, или чисто магнитной. При взаимодействии зарядов, движущихся в проводниках (электрических токов), кулоновское взаимодействие отсутствует вследствие электрической нейтральности проводника, и тогда преобладающим становится магнитное взаимодействие. В 1820 г. Ампер, исследуя взаимодействие проводников с током, установил, что сила f, приходящаяся на единицу длины двух параллельных проводников с токами I₁ и I₂, расположенных на расстоянии r друг от друга, удовлетворяет следующему соотношению f   . (5.1) В соответствии с (5.1) в СИ устанавливается единица силы тока  ампер (А). 1А  это такая сила постоянного тока, который, протекая по двум прямолинейным параллельным проводникам бесконечной длины и ничтожно малого поперечного сечения, расположенным на расстоянии 1 м друг от друга в вакууме, вызывает между ними силу 210^-7 Н на единицу длины. В СИ соотношение (5.1) записывается в виде , (5.2) где ₀  магнитная постоянная.  Исходя из определения 1А, найдем численное значение ₀. Подставляя в (5.2) значения I₁=I₂=1 А, r=1 м и f=1 Н/м, получаем ₀=410^-7 Н/А².  Как уже поминалось выше электрические и магнитные явления неразрывно связаны между собой, поэтому существует связь между электрической ₀ и магнитной ₀ постоянными. Можно показать, что  , где с  скорость света в вакууме.

Вектор магнитной индукции - это основная силовая характеристика магнитного поля (обозначается В). Пробный контур, помещенный в магнитное поле, испытывает со стороны магнитного поля действие вращающего момента сил М.

Опытным путем было установлено, что для одной и той же точки магнитного поля максимальный вращающий момент М (момент сил) пропорционален произведению силы тока I в контуре на его площадь S. Величину IS называют магнитным моментом контура Pm.

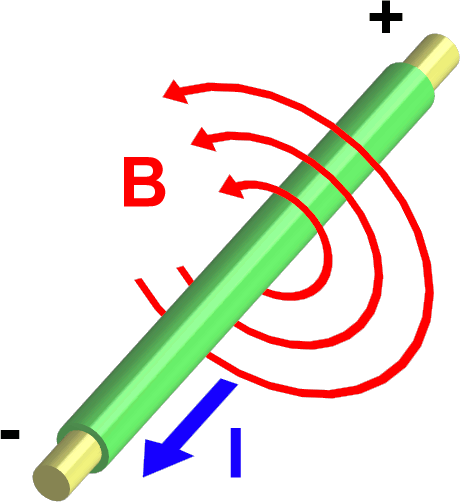
Вектор магнитной индукции (B).

ЛИНИИ МАГНИТНОЙ ИНДУКЦИИ  Электрическое поле характеризуется векторной величиной — напряженностью электрического поля. Надо бы ввести также и величину, характеризующую магнитное поле количественно. Дело это непростое, так как магнитные взаимодействия сложнее электрических. Векторную характеристику магнитного поля называют вектором магнитной индукции и обозначают буквой  . Сначала мы рассмотрим вопрос только о направлении вектора  . Магнитная стрелка. Мы видели, что в магнитном поле рамка с током на гибком подвесе, со стороны которого не действуют силы упругости, препятствующие ориентации рамки, поворачивается до тех пор, пока она не установится определенным образом. Вам известно, что так же ведет себя и магнитная стрелка — маленький продолговатый магнит с двумя полюсами на концах — южным S и северным N.  Направление вектора магнитной индукции. Ориентирующее действие магнитного поля на магнитную стрелку или рамку с током можно использовать для определения направления вектора магнитной индукции.

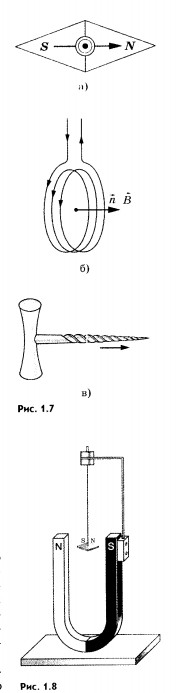
За направление вектора магнитной индукции принимается направление, которое показывает северный полюс N магнитной стрелки, свободно устанавливающейся в магнитном поле (рис. 1.7, а). Это направление совпадает с направлением положительной нормали к замкнутому контуру с током (рис. 1.7, б). Положительная нормаль направлена в ту сторону, куда перемещается буравчик (с правой нарезкой), если вращать его по направлению тока в рамке (рис. 1.7, в).

Используя рамку с током или магнитную стрелку, можно определить направление вектора магнитной индукции в любой точке поля.

На рисунках 1.8, 1.9 показаны опыты с магнитной стрелкой, повторяющие опыты с рамкой (см. рис. 1.5, 1.6).

В магнитном поле прямолинейного проводника с током магнитная стрелка в каждой точке устанавливается по касательной к окружности (см. рис. 1.9). Плоскость такой окружности перпендикулярна проводу, а центр ее лежит на оси провода.

Направление вектора магнитной индукции устанавливают с помощью правила буравчика: если направление поступательного движения буравчика совпадает с направлением тока в проводнике, то направление враш,ения ручки буравчика указывает направление вектора магнитной индукции.

Опыт по определению направления вектора индукции магнитного поля Земли проводит каждый, кто ориентируется на местности по компасу.  

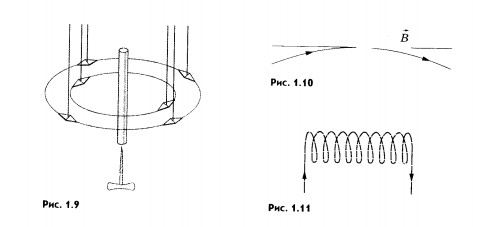
 Закон Био Савара Лапласа определяет величину модуля вектора магнитной индукции в точке выбранной произвольно находящейся в магнитном поле. Поле при этом создано постоянным током на некотором участке.

  Формулировка закона Био Савара Лапласа имеет вид: При прохождении постоянного тока по замкнутому контуру, находящемуся в вакууме, для точки, отстоящей на расстоянии r0, от контура магнитная индукция будет иметь вид.