Билет 1

Траектория – это линия, которую описывает матери-альная точка при движении. По форме траектории механические движения классифицируются на прямолинейные и криволинейные (рис. 5). Если траектория – прямая линия, то движение – прямолинейное. Если траектория – кривая линия, то движение – криволинейное.

Рис. 5

Вид траектории зависит от системы отсчета.

Путь S – это скалярная величина, равная длине траектории.

Путь всегда положительная величина. Положение материальной точки М в пространстве определяют три координаты x, y, z (прямоугольная декартова система координат) (рис. 7); на плоскости – две координаты x, y (рис. 8); на прямой линии – одна координата (рис. 1). При движении материальной точки ее координаты изменяются.

Рис. 7

Положение точки М может быть задано радиус-вектором (рис. 8). Радиус-вектор имеет три проекции, которые представляют собой координаты точки в данной системе координат: r_x= x, r_y = y, r_z = z.

Рис. 8

Радиус-вектор

Радиус-вектор   – это вектор, который соединяет начало координат с положением материальной точки на траектории.

При движении точки положение радиус-вектора изменяется (рис. 8):

₀ – начальный радиус-вектор;

 – конечный радиус-вектор.

Перемещение

Перемещением называется вектор  , соединяющий начальной положение материальной точки с ее конечным положением на траектории.

За промежуток времени   = (t – t₀) перемещение точки (рис. 8) равно (§ 18.2):

.

Перемещение – величина векторная. Векторы перемещения складываются геометрически: по правилу параллелограмма или по правилу треугольника (правило сложения векторов – § 18.1).

При прямолинейном движении в одном направлении путь S и модуль вектора перемещения   равны:

S = | |.

Рис. 9

При криволинейном движении (рис. 8)

.

Если  , то достаточно малое перемещение   (рис. 10) называется элементарным перемещением:  . Если компоненты этого вектора по трем осям соответственно равны  x,  y,  z, то абсолютная величина вектора   равна:

Рис. 10

На рис. 8:

Билет 2

Углово́е ускоре́ние — псевдовекторная физическая величина, характеризующая быстроту изменения угловой скорости твёрдого тела.

При вращении тела вокруг неподвижной оси, угловое ускорение по модулю равно^[1]:

Вектор углового ускорения   направлен вдоль оси вращения (в сторону   при ускоренном вращении и противоположно   — при замедленном).

При вращении вокруг неподвижной точки вектор углового ускорения определяется как первая производная от вектора угловой скорости   по времени^[2], то есть

,

и направлен по касательной к годографу вектора   в соответствующей его точке.

Существует связь между тангенциальным и угловым ускорениями:

,

где R — радиус кривизны траектории точки в данный момент времени. Итак, угловое ускорение равно второй производной от угла поворота по времени или первой производной от угловой скорости по времени. Угловое ускорение измеряется в рад/с² .

Углова́я ско́рость — векторная физическая величина, характеризующая скорость вращения тела. Вектор угловой скорости по величине равенуглу поворота тела в единицу времени:

,

а направлен по оси вращения согласно правилу буравчика, то есть, в ту сторону, в которую ввинчивался бы буравчик с правой резьбой, если бы вращался в ту же сторону.

Криволинейное движение – это всегда ускоренное движение. То есть ускорение при криволинейном движении присутствует всегда, даже если модуль скорости не изменяется, а изменяется только направление скорости. Изменение величины скорости за единицу времени – это тангенциальное ускорение:

или

Где v_τ, v₀ – величины скоростей в момент времени t₀ + Δt и t₀ соответственно.

Тангенциальное ускорение в данной точке траектории по направлению совпадает с направлением скорости движения тела или противоположно ему.

Нормальное ускорение - это изменение скорости по направлению за единицу времени:

Нормальное ускорение направлено по радиусу кривизны траектории (к оси вращения). Нормальное ускорение перпендикулярно направлению скорости.

Центростремительное ускорение – это нормальное ускорение при равномерном движении по окружности.

Полное ускорение при равнопеременном криволинейном движении тела равно:

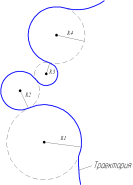
Движение тела по криволинейной траектории можно приближённо представить как движение по дугам некоторых окружностей (рис. 1.21).