28) Перспектива окружности, конуса, шестигранной призмы

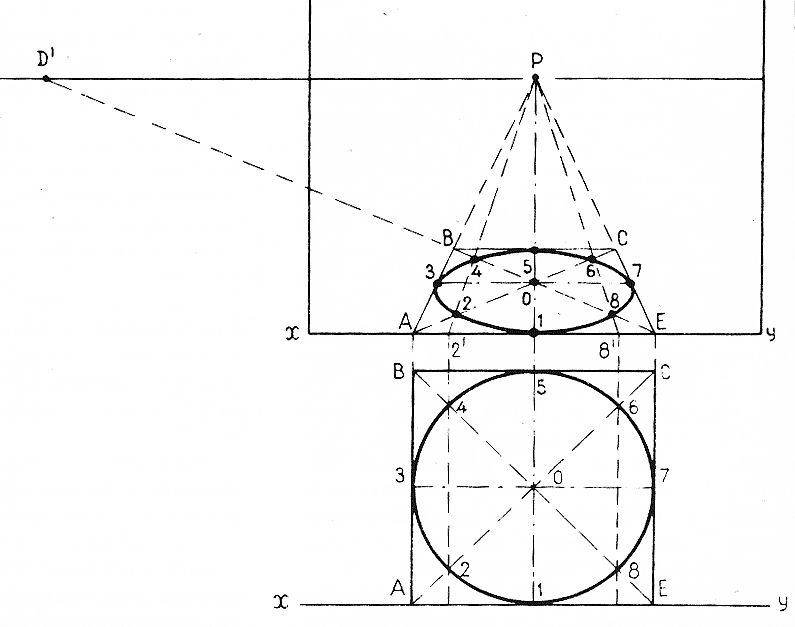
Перспектива окружности

При изображении окружности в перспективе можно использовать следующее построение: в плане строят квадрат, сторона которого равна диаметру изображаемой окружности. В этот квадрат вписывают окружность. Затем надо провести диагонали квадрата. Оси симметрии и диагонали разделят вписанную в квадрат окружность на восемь равных частей в точках 1,2... 7, 8, по которым и нужно строить окружность в перспективе. Спроецировав квадрат на основание картины и найдя его глубину в точках В и С, как это указано на ил. 96, построим его перспективное изображение и проведем в перспективе диагонали АС и ВЕ. В плане точки 3 и 7,1 и 5 лежат на пересечениях осей со сторонами квадрата, и их легко получить в перспективе. Для того чтобы найти точки 2 и 4, 6 и 8, нужно - спроецировать их на основание картины и последовательно соединить с точкой Р. Там, где прямые 2'—Р и 8'—Р пересекут диагонали квадрата, и будут искомые точки, по которым построим эллипс.

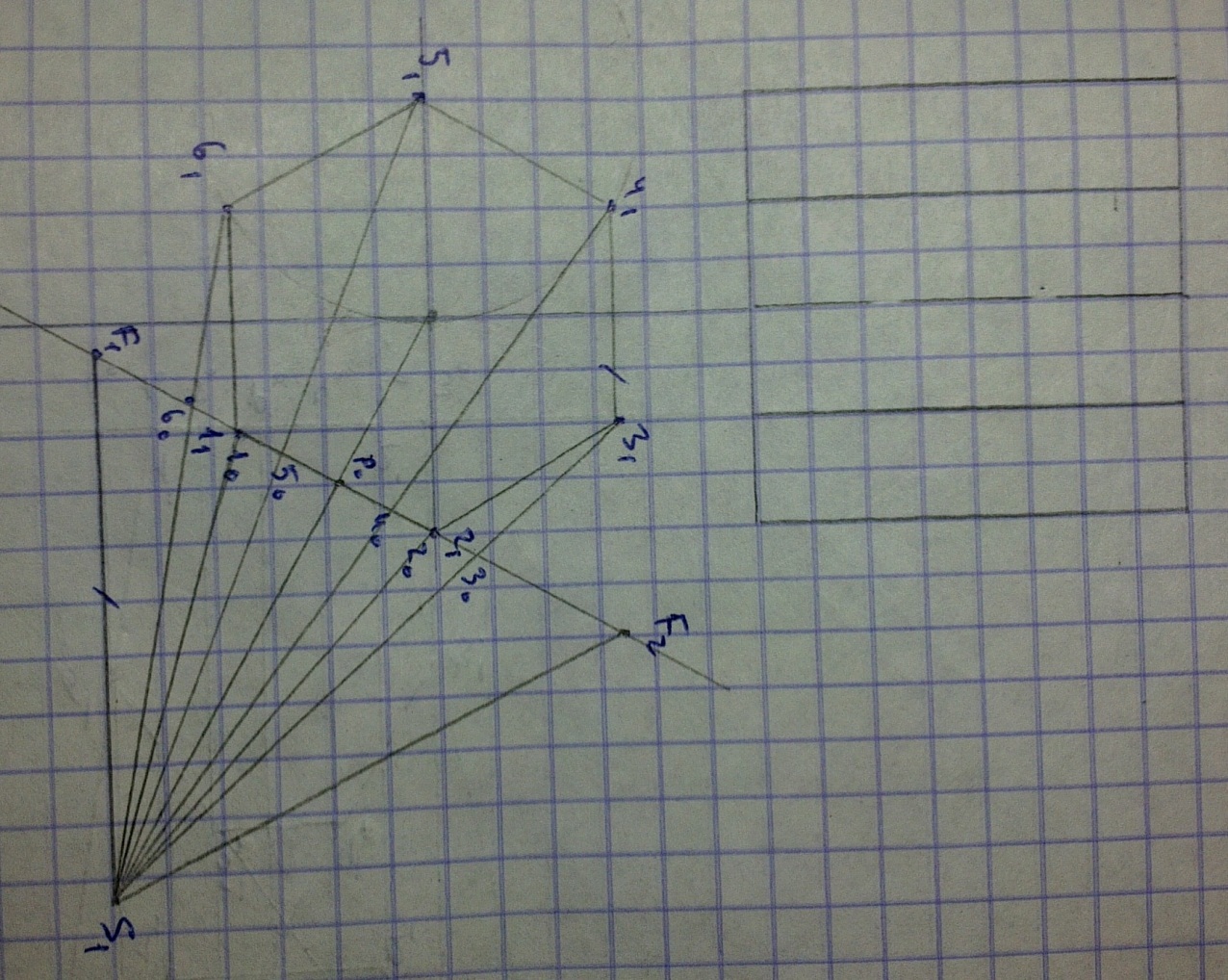
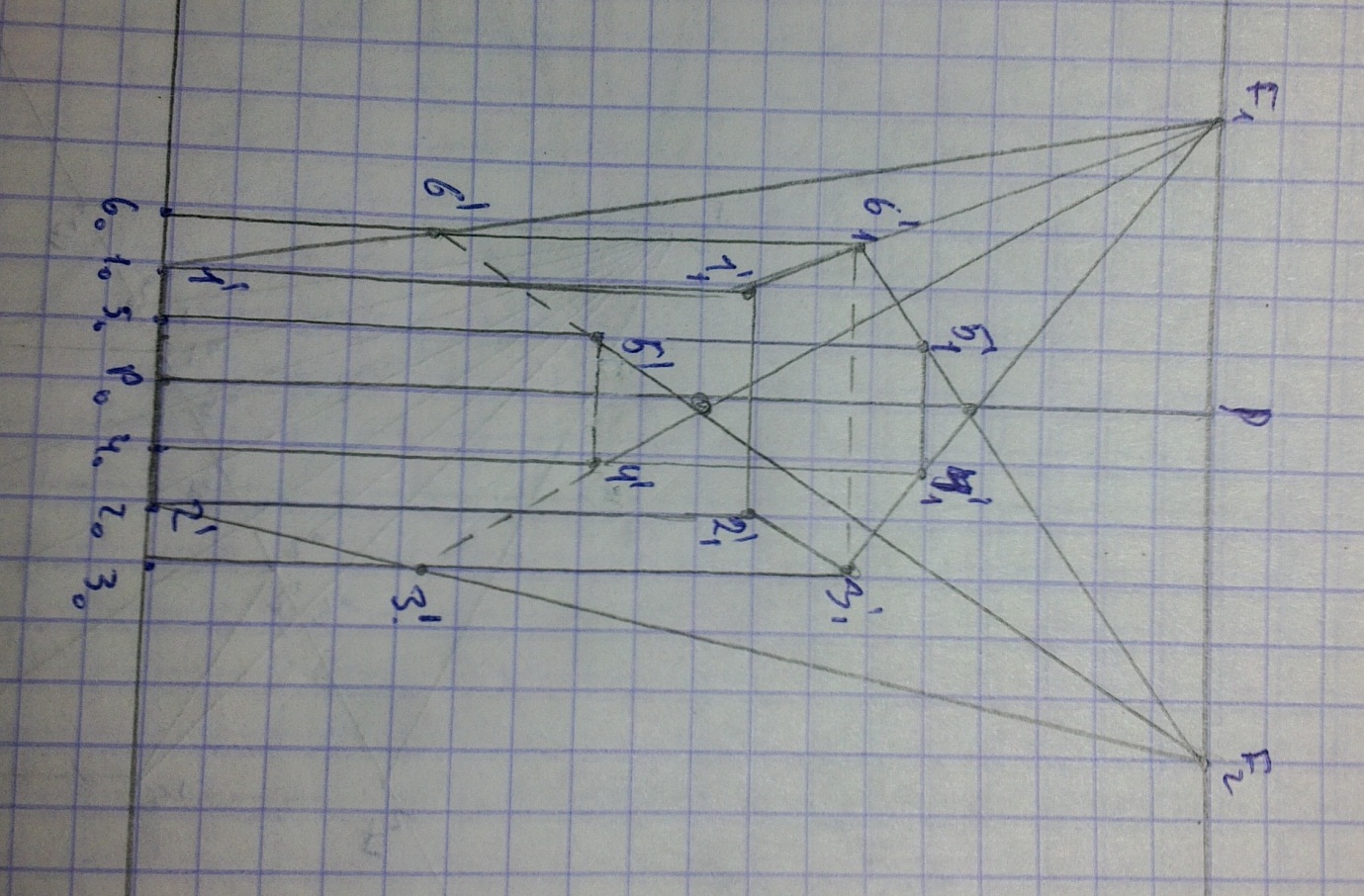
Перспектива шестигранной призмы

29)Тени в ортогональных проекциях прямых, плоскостей.

Тени в ортогональных проекциях

При построении теней обычно полагают, что свет распространяется прямолинейно. Если источник света удален от объекта на незначительное расстояние, освещение называется факельным. В том случае, когда источник света удален в бесконечность и световые лучи параллельны друг другу, освещение называют солнечным.

Чаше всего построение теней осуществляется при параллельных световых лучах. В этом случае за направление лучей света принимают направление диагонали куба, грани которого совмещены с плоскостями проекций П1, Г12, ПЗ. Вследствие этого проекции луча света совпадают с диагоналями квадратов, на чертеже образуют с осями проекций угол 45°

Падающая тень от прямой линии

Тень, падающая от прямой линии, состоит из падающих теней от всех ее точек. Лучи, проходящие через все точки прямой, образуют лучевую плоскость, а тень от прямой линии есть линия пересечения лучевой плоскости с плоскостью или поверхностью, на которую падает тень (то есть след лучевой плоскости).

Тенью, падающей от прямой на плоскость, является прямая линия, поэтому для ее построения достаточно построить тени от двух точек, принадлежащих этой прямой.

На рис. 77 построена тень на плоскости проекций от отрезка АВ на комплексном чертеже.

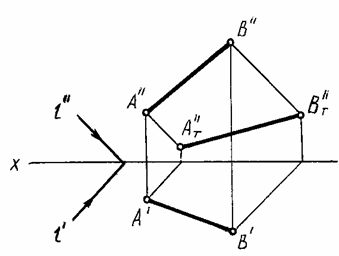
Тени от точек А и B в этом примере падают на одну плоскость проекций V, поэтому для построения тени отрезка АВ достаточно соединить между собой полученные точки АT'' и ВT'' прямой линией.

ПОСТРОЕНИЕ ТЕНИ ОТ ПЛОСКОЙ ФИГУРЫ

При построении падающей тени от плоской фигуры считают, что плоская фигура непрозрачна. Построение падающей тени от любой плоской фигуры сводится к построению падающих теней всех ее точек.

Рассмотрим пример построения тени плоского треугольника (рис.12.14), сторона ВС которого, лежит в горизонтальной плоскости проекций П1. В тех случаях, когда точка или прямая расположена в плоскостях проекций, задача несколько упрощается тем, что теней от этих точек и прямых строить не надо, в этом случае эти точки и прямые сами являются тенью. Для построения тени от данного треугольника надо найти тень только от точки А и соединить ее с горизонтальными проекциями точек В и С.

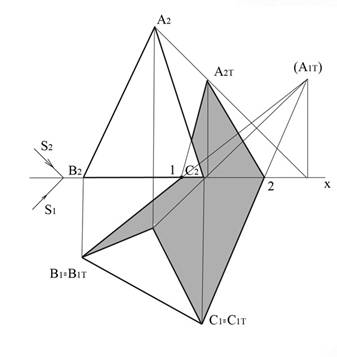
По общему правилу находим тень от точки А, которая падает на фронтальную плоскость проекций П2. Полученную тень А2т соединить с горизонтальными проекциями точек В и С нельзя, т.к. точки лежат в разных плоскостях проекций. Поэтому находим мнимую тень точки А на горизонтальной плоскости, предполагая, что плоскость П2 прозрачна, – точка (А1т). Найденную точку соединяем с основанием треугольника В1С1, в пересечении с осью Х находим точки преломления 1 и 2 тени треугольника, откуда тень перейдет на фронтальную плоскость проекций в точку А2т.