24) Пересечение плоскости с топографической поверхностью.

Линией пересечения любой поверхности плоскостью называется линия, соединяющая точки пересечения их горизонталей с одинаковыми отметками. Сечение топографической поверхности вертикальной плоскостью называется профилем. На рис. 14.4, а топографическая поверхность задана горизонталями (17, 18, 19, 20), плоскость – горизонтальным следом, совпадающим с направлением АВ. В точках пересечения прямой АВ с горизонталями поверхности восстанавливаем перпендикуляры, на которых откладываем отметки точек и соединяем их плавной линией. Профиль можно строить совмещенным с планом, можно вынести за пределы чертежа (см. рис. 14.4).

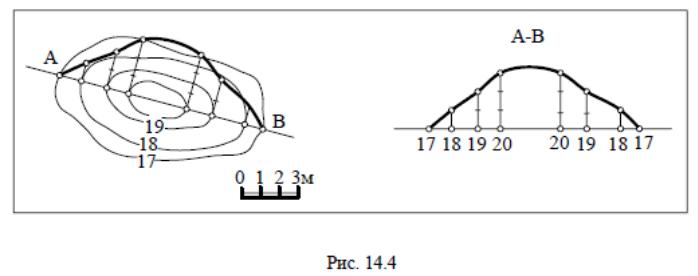
На рис. 14.5 дано построение профиля по линии Е-Е многогранной поверхности. Так как каждая грань поверхности является плоскостью, то достаточно спроецировать две точки с каждой грани, чтобы получить линию пересечения этой грани плоскостью.

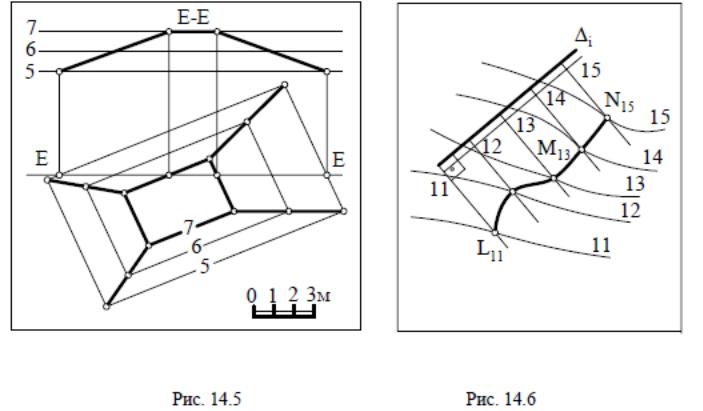
На рис 14.6 топографическая поверхность, заданная горизонталями 11 – 15, пересекается произвольной плоскостью, заданной масштабом уклона Δi. Изображаем плоскость Δ горизонталями, перпендикулярными масштабу уклона Δi, и находим точки пересечения одноименных горизонталей. Соединяем плавной линией полученные точки. Линия L11M13N15 является линией пересечения поверхности плоскостью.

25) Пересечение прямой с топографической поверхностью

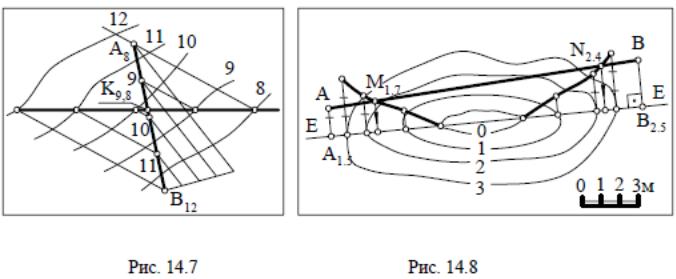
Чтобы построить точку пересечения прямой А8В12 с поверхностью, необходимо заключить прямую в плоскость общего положения (рис. 14.7). Для этого градуируем прямую А8В12 и через точки 8, 9, 10 и 11 проводим в произвольном направлении горизонтали, которыми задаем плоскость. Точки пересечения горизонталей с одинаковыми отметками соединяем плавной кривой. Полученная линия встречается с заданной прямой в искомой точке (К9,8). Для нахождения точки пересечения прямой с поверхностью можно

использовать другой способ. На рис. 14.8 дана прямая АВ, пересекающая топографическую поверхность. Все построения выполняем в следующем порядке:

1) заключаем прямую в вертикальную плоскость Е-Е;

2) строим профиль топографической поверхности;

3) спроецировав прямую на вспомогательную вертикальную плоскость, отмечаем фронтальные проекции точек пересечения прямой АВ с профилем топографической поверхности. Отметки точек определяем по их фронтальным проекциям (M1,7, N2,2).

26) Перспектива. Выбор аппарата перспективы.

Перспективой называют изображение (чертеж), образованное центральным проецированием фигуры-оригинала на плоскость и удовлетворяющее условиям, учитывающим особенности зрения. Этими условиями ограничивается взаимное положение точки зрения, фигуры-оригинала и плоскости проекций так, чтобы изображение фигуры было наиболее близким к ее зрительному восприятию в натуре.

К основным элементам перспективного аппарата относятся плоскость перспективных проекций , называемая картинной плоскостью или картиной, центр проецирования, или точка зрения , S и объект проецирования.

27) Перспектива плоской фигуры.

Плоскость в перспективе изображают чаще всего в виде плоской фигуры, ограниченной прямыми или кривыми линиями (плоскость стены здания, ската крыши, криволинейного фронтона, арки моста и т. д.). Поэтому построение перспективы плоскости сводится к построению перспектив и вторичных проекций прямых или кривых линий, ограничивающих плоскую фигуру.

На рис. 86 дана плоская фигура, представляющая собой очертание плана здания. Построение перспективы объемных предметов начинают с построения перспективы вторичных проекций предмета.

Существует множество способов построения перспективных изображений. Решим поставленную задачу методом архитекторов, который удобно применять в том случае, если изображение содержит семейства параллельных прямых.

Примечание.

Рекомендации по выбору элементов перспективы (точки зрения, картинной плоскости и линии горизонта) будут даны при построении объемного предмета.

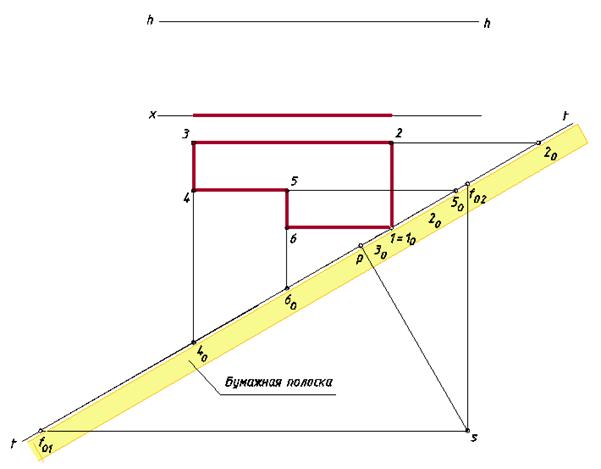
Проведем через вершину 1 картинную плоскость, которая на эпюре отобразится основанием t– t. Выберем точку зрения S, которая спроецируется на данном чертеже в точку стояния s.

У параллельных прямых, содержащих точки 1 – 6,5 – 4 и 2 – 3, общая несобственная точка F1 (на эпюре показана ее проекция на основании картины точка f01). Для ее нахождения из точки зрения Sпроводим луч, им параллельный до пересечения с картиной. Поскольку проведенный луч параллелен предметной плоскости его точка пересечения с картиной будет находиться на линии горизонта. Точка схода другого семейства прямых –точка F2.

Определим «начальные точки» всех прямых линий на основании картины 10, 20, 40, 50 и 60. Проведем главный луч картины. Построение перспективы картины начнем с ее основания t – t, проведя произвольную горизонтальную прямую t– t. С помощью бумажной полоски зафиксируем точки, построенные на эпюре, и перенесем их на картину (рис. 87). Построим линию горизонта параллельно линии t – tна расстоянии, взятом с эпюра (расстояние между осью x и h –h).

По точкам f01, f02 и p0 определяем F1, F2 и P на линии горизонта.

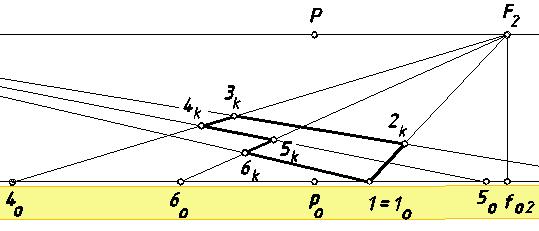
Строим перспективные изображения параллельных прямых с точками схода F1 иF2. Поскольку точки 1, 2, … 6 принадлежат одновременно двум семействам параллельных прямых, то на пересечении соответствующих определяем перспективные изображения точек 2к, 3к, 4к,52, и 6к. Соединив построенные точки соответствующим образом, получаем картину плоской фигуры.

Заметим, что центральную проекцию предмета можно построить при любых точках зрения (за исключением особых), любом положении картины и линии горизонта. Но при этом далеко не всегда полученное изображение будет наглядным. При построении перспективного изображения предмета необходимо соблюдать условия, при которых можно достичь желаемого результата.