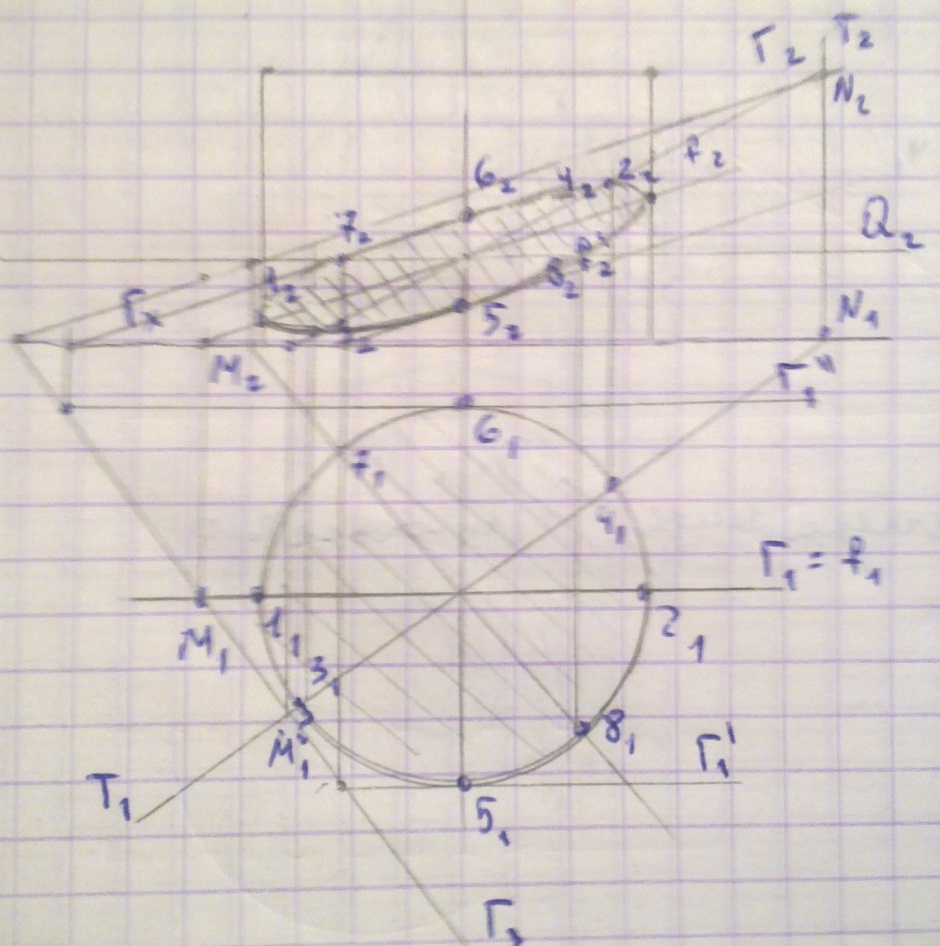
17) Построение сечения пов. Вращения плоскостью.

Определение проекций линий сечения следует начинать с построения опорных точек — точек, расположенных на очерковых образующих поверхности (точки, определяющие границы видимости проекций кривой); точек, удаленных на экстремальные (максимальное и минимальное) расстояния от плоскостей проекций. После этого определяют произвольные точки линии сечения.

Для нахождения общих точек, принадлежащих как поверхности, так и плоскости, целесообразно в качестве вспомогательных секущих поверхностей принять плоскости, перпендикулярные к оси вращения; в этом случае плоскости будут пересекать поверхность по окружностям, а плоскость по линиям уровня*. Определение точек сводится к нахождению точек пересечения прямой с окружностью.

Пример. Пересечение цилиндра плоскостью

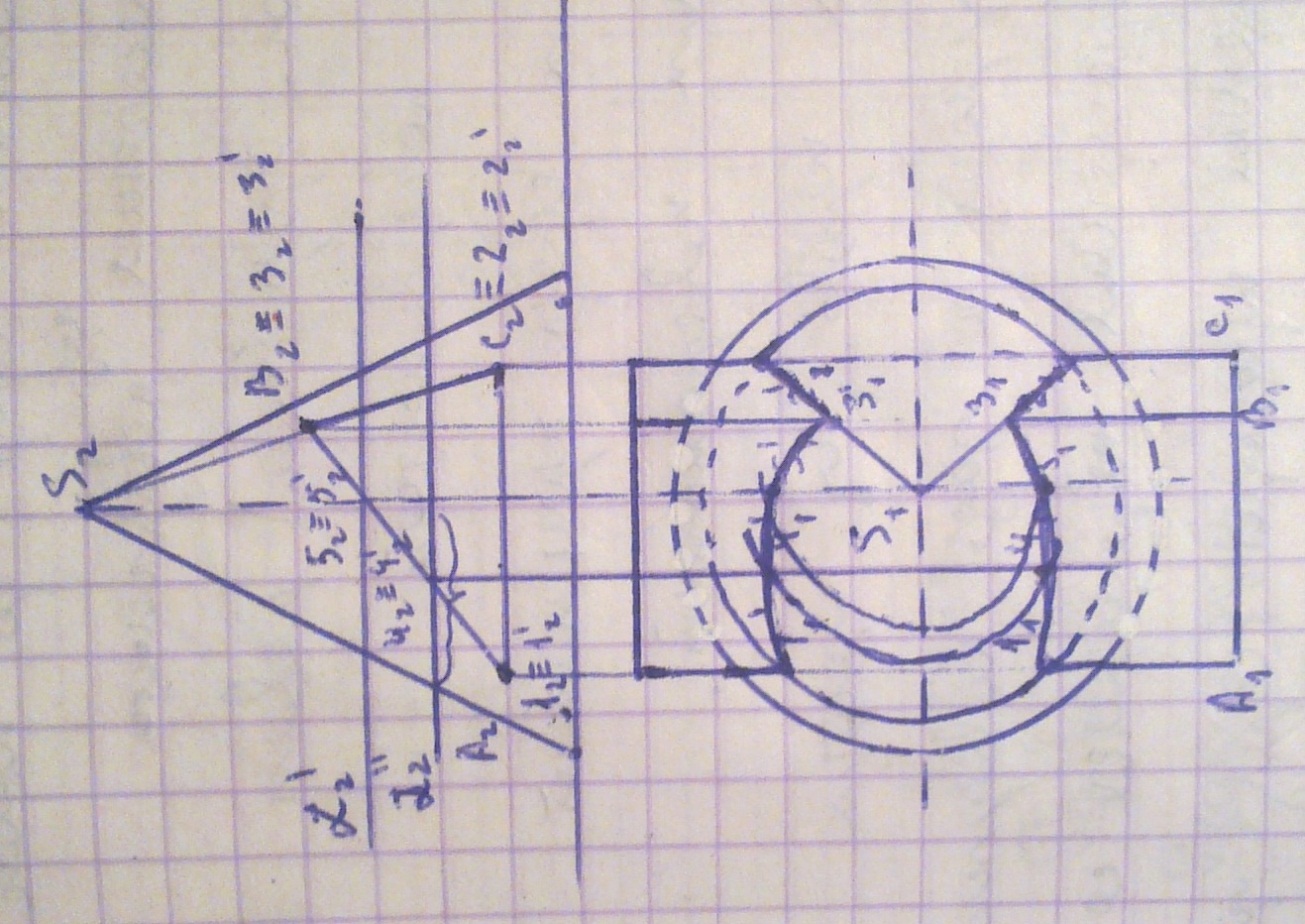
18) Построение линии пересечения двух поверхностей способом вспомогательных секущих плоскостей.

Суть метода заключается в том, что вводят вспомогательную плоскость (желательно частного положения). Строим линию пересечения вспомогательной плоскости с каждой из заданных поверхностей, на пересечении этих линий находят точки, общие для заданной поверхности, которые потом соединяют.

Пример. Построение линии взаимного пересечения конуса и призмы.

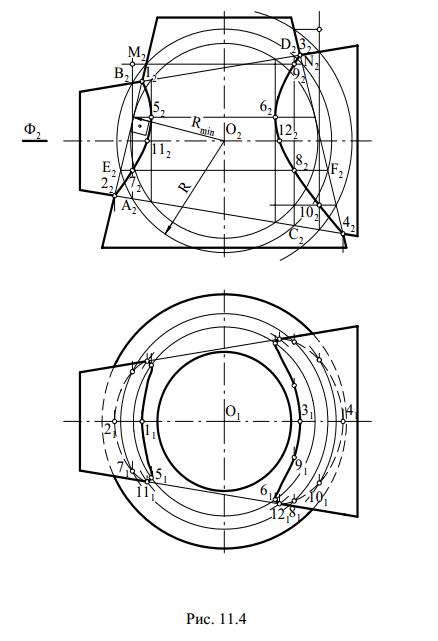
19) Построение линии пересечения двух поверхностей способом вспомогательных концентрических сфер.

Применяется:

для построения линии взаимного пересечения поверхностей в том случае, если обе пересекающиеся поверхности являются поверхностями вращения и оси пересекаются, и задают плоскость симметрии параллельную одной из плоскостей проекций.

Максимальный радиус вспомогательной сферы равен расстоянию от центра вспомогательных сфер до наиболее удаленной точки линии пересечения заданной поверхности.

Минимальный радиус вспомогательных сфер равен большей из нормалей заданных поверхностей.

За центр вспомогательных сфер принимают точку пересечения осей заданных поверхностей.

Нормаль – это прямая проведенная из центра вспомогательных сфер к образующей заданной поверхности.

Если какая-то поверхность вращения пересекается со сферой и ось поверхности вращения проходит через центр сферы, то линия пересечения поверхности вращения со сферой будет окружность, плоскость которой перпендикулярна оси поверхности вращения.

20)Заложение, превышение, уклон, интервал, н.В.Прямой и угол наклона прямой к пл нулевого уровня. Градуирование прямой.

Длина горизонтальной проекции отрезка прямой называется заложением прямой.

Превышение – разность отметок вершин.

Отношение разности высотных отметок концов отрезка прямой к его заложению называется уклоном.

Горизонтальная проекция отрезка между двумя точками прямой, имеющими разность уровней в одну единицу, называется интервалом прямой.

Определение угла наклона линии выполняется с помощью циркуля или полоски бумаги. Для определения угла наклона линии нужно взять циркулем или отметить на краю полоски бумаги расстояние по данному направлению между горизонталями, разность значений высот которых равна высоте сечения рельефа, подписанного на шкале заложений. Совмещают одну из ножек циркуля (одну из меток на полоске бумаги) с основанием шкалы заложений и устанавливают раствор циркуля (край полоски бумаги) перпендикулярно основанию шкалы заложений. Перемещают циркуль (полоску бумаги) влево и вправо по шкале заложений, удерживая ножку (метку на полоске бумаги) на основании шкалы заложений, до совпадения второй ножки (метки на полоске бумаги) с плавной кривой. Значение искомого угла наклона линии определяю путем простой интерполяции подписанных ближайших слева и справа от циркуля (края полоски бумаги) значений углов наклона.

Градуирование прямой. Под градуированием прямой понимается определение точек прямой с отметками, выраженными целыми числами и отличающимися друг от друга на единицу длины. Здесь возможны два случая:

а. Когда оба конца отрезка имеют одинаковые знаки. В этом случае от конца отрезка с большей отметкой откладывают, перпендикулярно к нему, значения разности отметок и проводят графическое градуирование. Если концы отрезков имеют дробные отметки, то от конца отрезка с меньшей отметкой откладывают только дробную часть, а от другого - разницу отметок плюс дробную часть отметки конца отрезка.

б. Случай, когда концы отрезков имеют разные знаки. Построения отличаются лишь тем, что отметки начала и конца отрезка откладываются в противоположные стороны.