12) Способ замены плоскостей проекций

Суть способа заключается в том, что геометрический образ остается на месте, а меняют свое положение плоскости проекций. При этом вновь вводимая плоскость должна быть перпендикулярна к той плоскости, которая остается и на новой плоскости откладываются координаты с той плоскостью, которую мы заменяем.

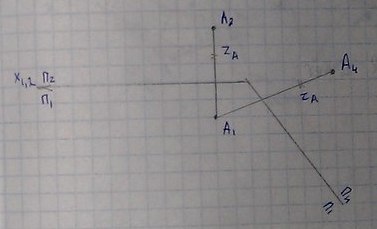
Определение н.в. отрезка АВ

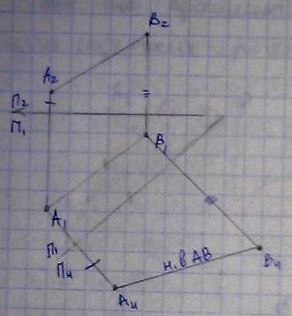
Определить н.в. треугольника АВС

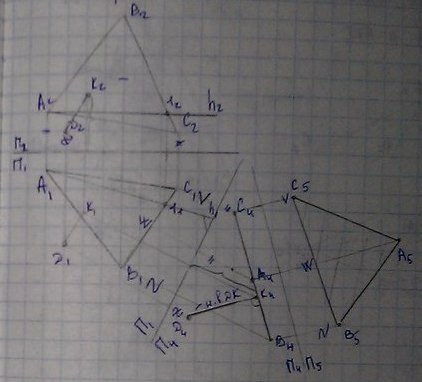
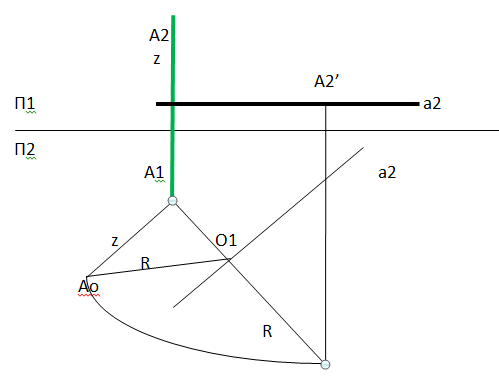
13) Способ вращения вокруг линий уровня.

Этот способ применяется в основном для решения задачи преобразования плоскости общего положения в плоскость уровня. Суть способа заключается в том, что плоскость общего положения, поворачивается вокруг прямой уровня до состояния, параллельного горизонтальной плоскости проекций П1 либо фронтальной П2

14) Построение точек пересечения прямой с многогранником

Прямая линия может пересекать поверхность многогранника в двух точках при условии, что многогранник выпуклый. Решение этой задачи основано на схеме определения точки пересечения прямой с плоскостью и распадается на три этапа:

1) через заданную прямую проводится вспомогательная плоскость;

2) строится проекция фигуры сечения многогранника;

3) определяются точки пересечения прямой с контуром сечения.

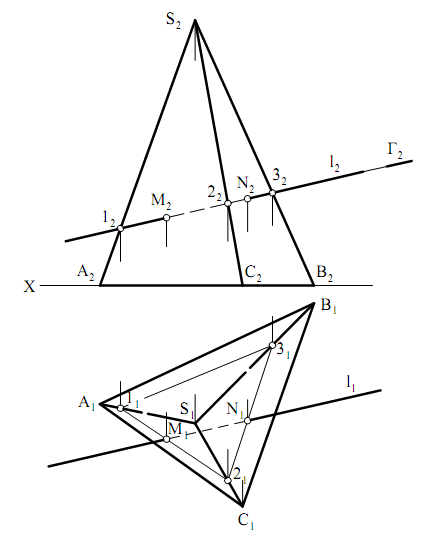
На рис. 8.11 построены точки M (М1, М2) и N (N1, N2) пересечения

прямой l с поверхностью пирамиды SABC.

15) Построение сечения многогранника плоскостью

При пересечении многогранника плоскостью в общем случае получается плоский многоугольник АВСD . Этот многоугольник можно построить или по точкам пересечения с плоскостью ребер многогранника, или по линиям пересечения граней многогранника с плоскостью. Следовательно, задача сводится к определению точек пересечения прямой с плоскостью или к определению линий пересечения плоскостей. Первый способ на практике применяется чаще второго. Плоскую фигуру, полученную от пересечения многогранника плоскостью, называют сечением.

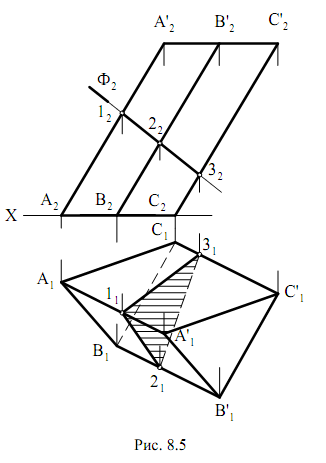
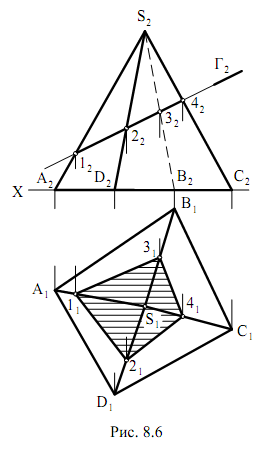
Эти построения можно выполнять двумя способами:

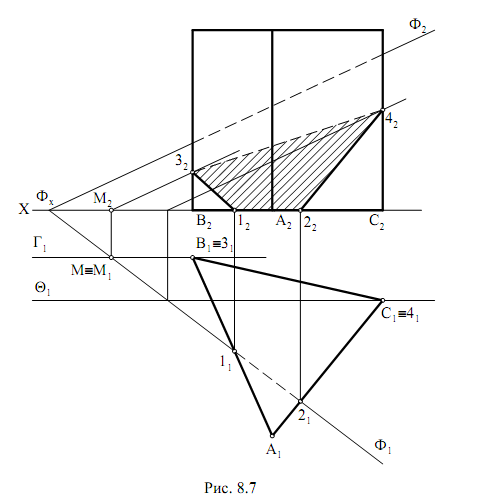
а) метод ребер(8.7) – нахождение точек пересечения ребер многогранника с плоскостью, т.е. нахождение вершин многогранника, получающегося в сечении;

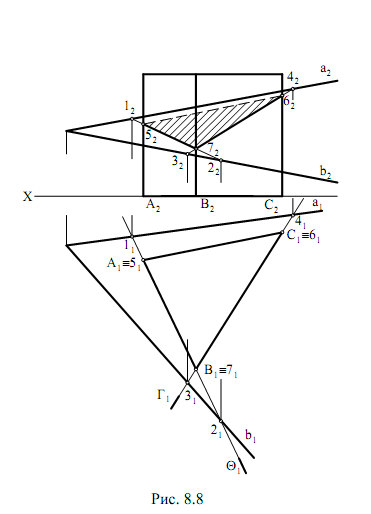
б) метод граней(8.8) – нахождение линий пересечения граней многогранника с секущей плоскостью, т.е. нахождение сторон сечения.

16) Построение точек пересечения прямой с пов. Вращения.

Чтобы построить точки пересечения прямой с поверхностью вращения необходимо:

1.Прямую заключить во вспомогательную плоскость.

2.Построить сечение поверхности вспомогательной плоскости.

3.Отметить точки пересечения заданной прямой с построенным сечением

Пример.

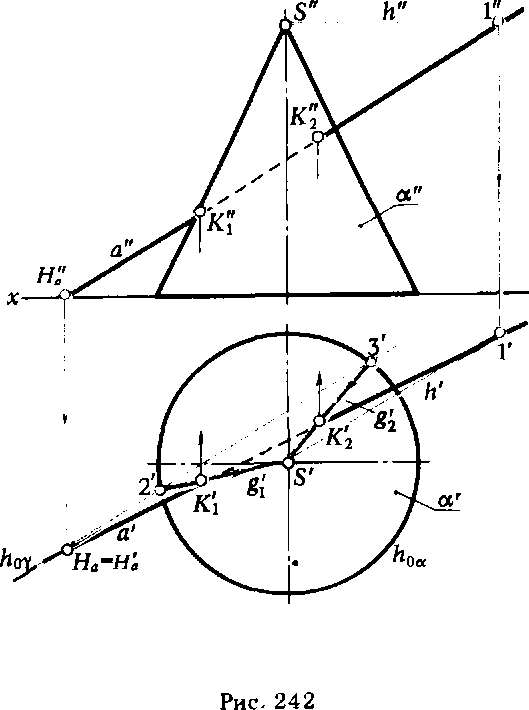
Определить точки пересечения прямой а с поверхностью прямого кругового конуса а.

РЕШЕНИЕ. Заключаем прямую а в плоскость у, проходящую через вершину конической поверхности S. На рис. 242 плоскость у задана пересекающимися прямыми а и h , при этом h — горизонталь.

Определяем горизонтальный след плоскости 7; для этого находим горизонтальный след прямой На и через него проводим hо 7 параллельно горизонтальной проекции горизонтали h1. Отмечаем точки 2' и 3', в которых h 0у Oft оа. (S'2'j и (S'3') — образующие поверхности а, по которым она пересекается плоскостью у.

Точки К\ и К'2 (К\ = а' П (S'2') и К'2 = = а' П (S'3')) — горизонтальные проекции искомых точек пересечения. Зная положение К\ и К2, определяем К" и К2.