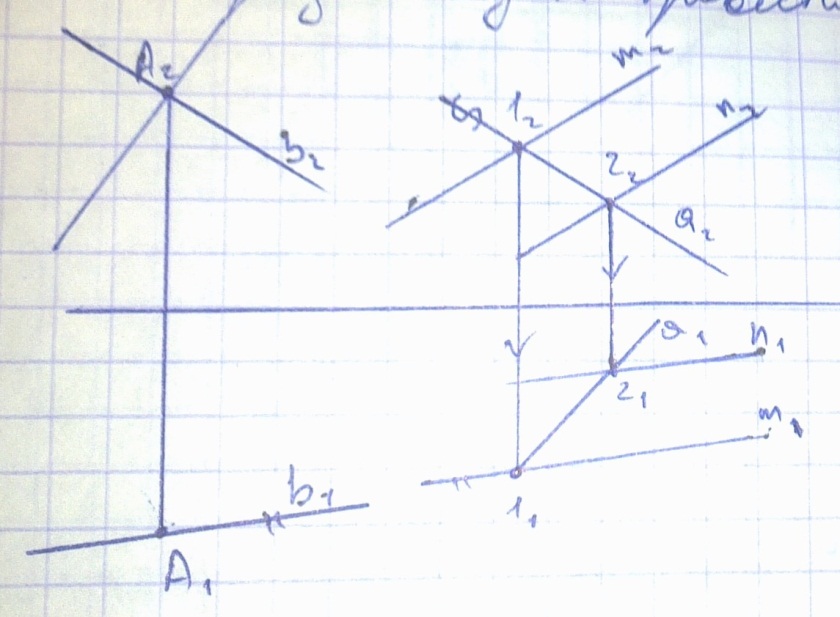
- •1)Проецирование точки на 2 и 3 взаимноперп.Пл. Проекций.
- •2) Прямая. Классификация прямых
- •3) Определение н.В. Прямых и углов наклона к пл-ям проекций
- •4) Пл. Общего и частного положения.
- •5) Главные линии плоскости.
- •6) Определение углов наклона пл. К плоскостям проекций.
- •7) Следы прямых и плоскостей.
- •8) Пересечение прямой с пл. Частного и общего положения.
- •9) Пересечение плоскостей общего положения.
- •10) Прямые перпендикулярные к плоскости. Перпендикулярность плоскостей.
- •11) Прямая ll плоскости. Параллельность плоскостей
- •12) Способ замены плоскостей проекций
- •13) Способ вращения вокруг линий уровня.
- •14) Построение точек пересечения прямой с многогранником
- •15) Построение сечения многогранника плоскостью
- •16) Построение точек пересечения прямой с пов. Вращения.
- •17) Построение сечения пов. Вращения плоскостью.
- •18) Построение линии пересечения двух поверхностей способом вспомогательных секущих плоскостей.
- •19) Построение линии пересечения двух поверхностей способом вспомогательных концентрических сфер.
- •20)Заложение, превышение, уклон, интервал, н.В.Прямой и угол наклона прямой к пл нулевого уровня. Градуирование прямой.
- •21) Пересечение плоскостей в проекциях с числовыми отметками
- •22) Пересечение прямой с плоскостью в проекциях с числовыми отметками.
- •23) Топографическая поверхность. Построение профиля топ.Пов.
- •24) Пересечение плоскости с топографической поверхностью.
- •25) Пересечение прямой с топографической поверхностью
- •26) Перспектива. Выбор аппарата перспективы.
- •28) Перспектива окружности, конуса, шестигранной призмы
- •29)Тени в ортогональных проекциях прямых, плоскостей.
- •30) Построение теней в ортогональных проекциях геометрических тел.
- •31) Развёртка, метод нормального сечения.
8) Пересечение прямой с пл. Частного и общего положения.
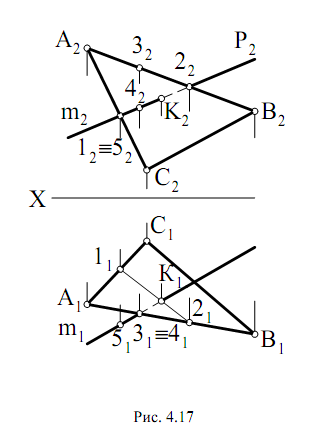
Чтобы определить точку пересечения прямой m с плоскостью, заданной треугольником АВС, необходимо выполнить следующее:
- провести через прямую m фронтально-проецирующую плоскость Р (Р2);
- определить линию пересечения плоскости Р и треугольника АВС 12 (1222 и 1121);
- определить точку пересечения прямой m (m1, m2) с треугольником АВС. Эта точка находится на линии пересечения плоскостей Р и треугольника АВС – 12 (1121 и 1222). Сначала определяем горизонтальную проекцию К1, а затем фронтальную К2.
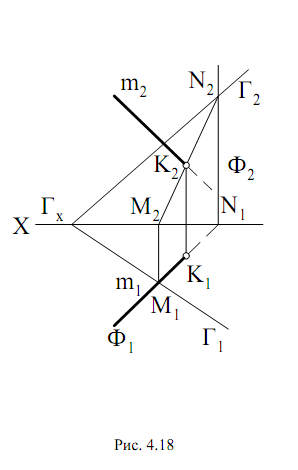
При определении точки пересечения прямой m с плоскостью, заданной следами Г1 и Г2 (рис. 4.18), необходимо также прямую m заключить в горизонтально-проецирующую плоскость Ф (Ф1 и Ф2) и найти их линию
пересечения MN (M1N1 и M2N2). Фронтальная проекция точки пересечения прямой К2 будет находиться на фронтальной проекции линии пересечения
M2N2, горизонтальная проекция К1 находится при помощи линии связи.
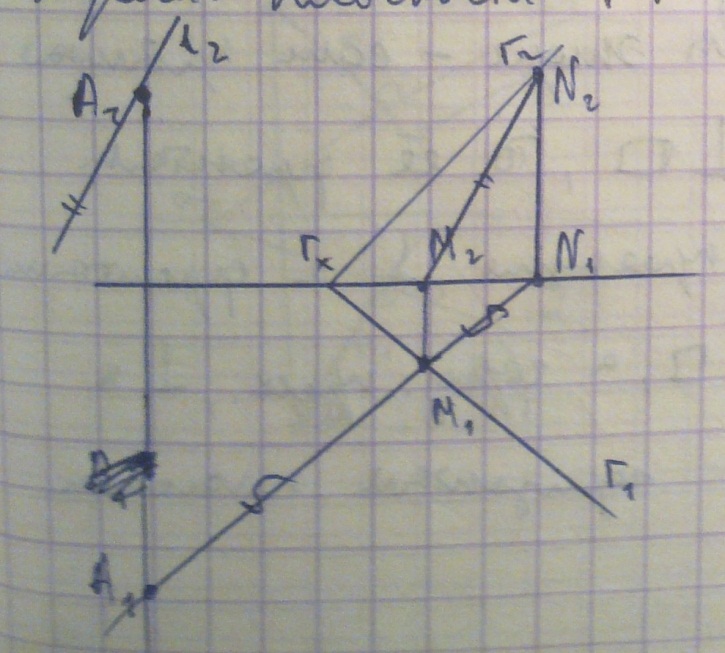
9) Пересечение плоскостей общего положения.
Точка N является фронтальным следом линии пересечения плоскостей, а точка М – горизонтальным следом линии пересечения. Одновременно в этих точках находятся и соответствующие проекции этих следов
N2 и M1. Так как точка N2 находится во фронтальной плоскости проекций, то горизонтальная проекция N1 будет находиться на оси Х. Аналогично и с точкой М (М1 и М2). Соединяя прямыми линиями одноименные проекции
точек М1 с N1 и М2 с N2, получим проекции прямой MN – линии пересечения плоскостей Г и Р.

10) Прямые перпендикулярные к плоскости. Перпендикулярность плоскостей.
Прямая называется перпендикулярной плоскости, если она перпендикулярна любой прямой, лежащей в этой плоскости.
Теорема. (Признак перпендикулярности прямой и плоскости.) Если прямая перпендикулярна двум пересекающимся прямым плоскости, то она перпендикулярна и самой плоскости. На эпюре, если прямая перпендикулярна плоскости, то ее фронтальная проекция перпендикулярна к фронтальной плоскости, а горизонтальная проекция к горизонтальной плоскости.
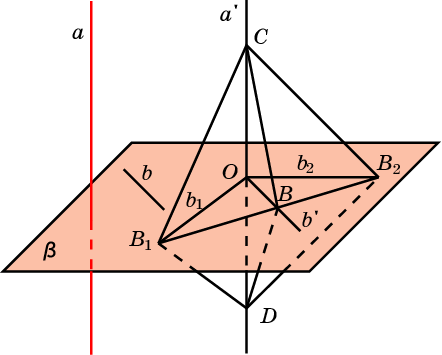
Две плоскости называются перпендикулярными, если угол между ними прямой.
Теорема. (Признак перпендикулярности двух плоскостей.) Если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.
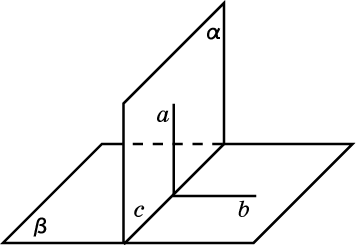
11) Прямая ll плоскости. Параллельность плоскостей
Прямая параллельна плоскости, если она параллельна какой-либо прямой лежащей в этой плоскости.
Через точку А провести прямую общего положения параллельно плоскости Г.
Две плоскости параллельны, если две пересекающиеся прямые одной плоскости паралл ельны двум пересекающимся прямым другой плоскости.
Через точку А провести плоскость параллельно заданной другой плоскости.