24. Восстановление функций по мнк.

Задача о сглаживании экспериментальных зависимостей. Пусть зависимость между двумя переменными x и y выражается в виде таблицы, полученной опытным путем. Это могут быть результаты опыта или наблюдений, статистической обработки материала и т.п.

x	x1	x2	...	xi	...	xn
y	y1	y2	...	yi	...	yn

Требуется наилучшим образом сгладить экспер-ную зависимость между переменными x и y, т.е. по возможности точно отразить общую тенденцию зависимости y от x, исключив при этом случайные отклонения, связанные с неизбежными погрешностями измерений или статистических наблюдений. Такую сглаженную зависимость стремятся представить в виде формулы y=f(x). Формулы, служащие для аналитического представления опытных данных, получили название эмпирических формул. Зад. нахождения эмпирических формул разбивается на два этапа. На первом этапе нужно установить вид зависимости y=f(x), т.е. решить, является ли она линейной, квадратичной, логарифмической или какой-либо другой. Второй этап – определение неизвестных параметров этой ф-и.

Часто вид эмпирической зависимости известен, но числовые параметры неизвестны. Будем считать, что зависимость полиномиальная, а для определения параметров полинома рассмотрим метод.МНК. Пусть y=f(x) задана таблицей своих значений: y_i=f(x_i) ,i=0,..,n Требуется найти многочлен фиксированной степени m для которого среднеквадратичное отклонение (СКО)

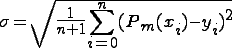
мин-но. Так как многочлен P_m(x)=a₀+a₁x+a₂x²+…+a_mx^m

определяется своими коэф, то фактически нужно подобрать набор коэфф a₀,…, a_m мин-щий ф-ю

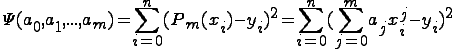
Используя необх условие экстремума,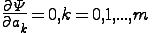 получаем так наз. нормальную с-му МНК:

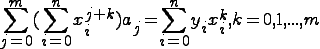Полученная с-ма есть с-ма алгебраических ур-й относительно неизвестных a₀,a₁..a_m. Можно показать, что определитель этой системы отличен от нуля, то есть решение существует и единственно. Однако при высоких степенях m система является плохо обусловленной. Поэтому метод наименьших квадратов применяют для нахождения многочленов, степень которых не выше 5. Решение нормальной системы можно найти, например, методом Гаусса. Запишем нормальную с-му наимен квадратов для двух простых случаев:m=0 и m=2. При m=0 мн-лен примет вид: P₀(x)=a₀. Для нахождения неизвестного коэфф a₀ имеем ур-ие:

_.

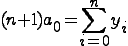Получ, что коэф a₀ есть среднее арифметическое знач ф-ции в заданных точках.

Если же используется мн-лен 2 степени P₂(x)=a₀+a₁x+a₂x²то нормальная с-ма у-ний примет вид:

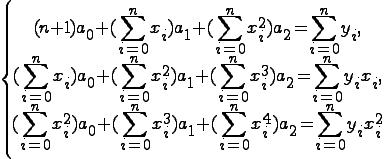
26 Полиномы Чебышева(пч)

Из всех полиномов степени n со старшим коэф 1 ПЧ отклоняющийся от 0 на отрезке [-1;1].

Мн-ном Чебышева наз-ся ф-ция: T_n(x) = cos(n*arcos(x)), n из N, x из [-1;1].n=0, T₀=1 n=1, T₁(x)=x.

α = arcos(x) -> T_n-1 = cos((n-1)* α), T(_n+1) = cos((n+1)* α)

cos((n+1)*α) = cos(n*α)*cos(α) – sin(n*α)*sin(α)

cos((n-1)*α) = cos(n*α)*cos(α) + sin(n*α)*sin(α)

cos((n+1)*α)+ cos((n-1)*α) = 2* cos(n*α)*cos(α)

T_n+1(x)+T_n-1(x) = 2xT_n(x) => (2) T_n+1(x) = 2xT_n(x)-T_n-1(x)

T₂(x) = 2x²-1;T₃(x) = 2x(2x²-1)-x = 4x³-3x

Анализ формулы (2) позволяет утверждать след:

1.все ф-ции многочлены степени n;2.все степени возростают с ростом n, старший коэфф имеет вид 2^n-1xⁿ ;3.при четн эн все степени четные.

Св-ва:1.многочлен имеет на [-1;1] ровно эн различн действ корней;2.корни ПЧ перемежаются с точками их наиб и наим знач = -1 и 1;3.из всех мн-нов степ эн нормир ПЧ отклоняется от 0 наим на [-1;1].

T_n(x) –нормиров.ПЧ.

Т.Мн-н Чебышева T_n(x),а также [-1;1] ровно n различных корней, кот задаются x_k = cos( )