17. Численное интегрирование. Формулы Ньютона-Котесса

Если ф-ция задана таблично, или интеграл неберущийся, то прим. числ. интегр. Простейшие ф-мы: ф-ла трапеций и ср-х прямоуг-в. Ф-ла Ньют-Кот:∫f(x)dx=∑Ai f(xi)+R, Ai-квадратурные коэф, xi-квадр-е узлы. Рассм. ∫f(x)dx=∫(Pn(x)-Rn(f,n))dx=∫Pn(x)dx+Rn. Расм. равном-ю сетку:X1=a, Xn=b, h=(b-a)/n, Xi=Xo+ih, t=(x-xo)/h, dx=h dt, ω(x)=(x-xo)(x-x1)…(x-xn)=th(t-1)h(h-2)h…(t-n)h=hⁿ⁺¹П(t); ω’(t)=ih(i-1)h…h(-h)(-2h)…(-(n-i))h=i!hⁱ(n-i)!h^n-i(-1)^n-i=hⁿi!(n-i)!(-1)^n-I. Ai=(b-a)Bi, Bi=((-1)^n-i/ni!(n-i)!)*∫П(t)dt/(t-i)-коэф Ньют-Кот, не зависит от подинт. ф-ции, обл. итегрир, числа точек n.Пусть n=1,f(x0)=f(a), f(x1)=f(b), Bo=1/2, B1=1/2: ∫f(x)dx=(b-a)∑Bi f(xi)+R1=((b-a)/2)*(f(a)-f(b))+R1-ф-ла трапеции

18. Малая и большая формула трапеций и её остаточный член

Заменим ф-цию на отрезке [a;b] многочленом Лагранжа 1-й степени с узлами х0=а, х1=b. (1)F=∫f(x)dx≈((b-a)/2)*(f(a)-f(b)). Для нахождения погр-ти разл f(x) по ф-ле Тейлора: f(x)=f(x*)+(x-x*)f(x’)+0.5(x-x*)²+…, х*=0.5(a+b). Член погрешности R=∫f(x)dx-((b-a)/2)*(f(a)-f(b)) ≈-(b-a)³f’’(x*)/12. Интеграл разбивают на сумму инт-в по шагам сетки и к каждому шагу применяют ф-лу(1), получ обобщ-ю ф-лу трапеций ∫f(x)dx≈∑(Xi-Xi-1)(f i-1 +fi)/2, R≈-∑(Xi-Xi-1)³f’’’(x*i)/12. На равномерной сетке она упрощается: ∫f(x)dx≈ h(fo/2+ f1+f2+…+f N-1+f N), R≈-∑h³f’’’(x*i)/12≈-h²∫f’’’(x)dx/12, h=Xi-Xi-1. Для справедливости этой оценки необх существ-ние непрер-й f’’’(x), если она кус-но-непр-на, то |R|≤(b-a)h²M₂/12, M₂ =max|f’’’(x)|.

19. Малая и большая формула средних прямоугольников и ее остаточный член.

Рассм. простейшие ф-лы приближенного интегрирования

; ф-ла левых прямоугольников

ф-ла правых прямоугольников; ф-ла средних прямоугольников.Пусть ,

(1)

(2)

; ;

(3).Пусть ,

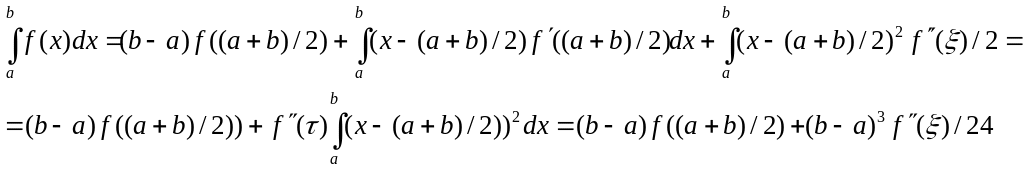
(5)

Разобьем [a;b] на n частей и к каждой применим свою ф-лу пр-ков. (6) –большая ф-ла пр., где h=(b-a)/2

При , (6) - ф-ла л.пр-ков; при , (6) - ф-ла пр.пр-ков; при (6) - ф-ла ср.пр-ков.

20.Формула Симпсона

В этом методе предлагается подынтегральную функцию на частичном отрезке аппроксимировать параболой, проходящей через точки (x_j, f(x_j)), где j = i-1; i-0.5; i, то есть подынтегральную функцию аппроксимируем интерполяционным многочленом Лагранжа второй степени:

(2.14)

Проведя интегрирование, получим:

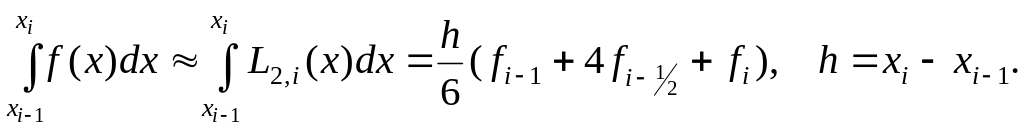(2.15)

Это и есть формула Симпсона или формула парабол. На отрезке [a, b] формула Симпсона примет вид

(2.16)

Избавимся в выражении (2.16) от дробных индексов, переобозначив переменные:

(2.17)

Тогда формула Симпсона примет вид

(2.18)

Погрешность формулы (2.18) оценивается следующим выражением:

, (2.19)

где h·n = b - a,

Таким образом, погрешность формулы Симпсона пропорциональна O(h⁴).

Замечание. Следует отметить, что в формуле Симпсона отрезок интегрирования обязательно разбивается на четное число интервалов.

21.Квадратурные формулы более высокого порядка точности

Дальнейшее повышение порядка точности формул, подобных квадратурным формулам центральных прямоугольников, трапеций, парабол, можно получить, применяя на отрезках разбиения интерполяцию функции f(x) многочленами более высокой степени (ниже мы использовали линейные функции, то есть многочлены степени 1, и квадратные трёхчлены -- многочлены степени 2).

Например, если использовать кубическое интерполирование, то есть приближать функцию f(x) многочленами степени 3, то получится формула, называемая кквадратурной формулой 3/8 (три восьмых)":

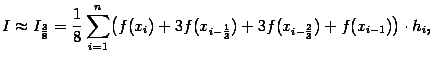
где h_i=x_i-x_i-1; x_i-1/3=x_i-1/3h_i; x_i-2/3=x_i-2/3h_i

т е точки x_i-2/3 и x_i-1/3 делят отрезок разбиения [x_i-1;x_i]на три равных части. Число 3/8 в названии формулы связано с тем, что если положить h=h_i=(b-a)/n постоянным и ввести обозначение , то формула получает вид

23. Правило Рунге — Ромберга . Пусть у_k^(h) и у_2k^(2h) — значения искомой функции, полученные одним из указаний выше методов при шагах вычисления h и 2h соответственно, а ε — заданная абсолютная предельная погрешность Тогда считается, что достигнута заданная точность вычислений, если выполняется неравенство

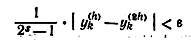(5)

при всех k и при s = 2, 3, 4 соответственно для методов Эйлера, Эйлера с итерациями и Рунге — Кутта. Решением задачи является функция {y_k^(h)}.

Применяя указанное правило, последовательно вычисляют значения искомой функции с шагом 2h и с шагом h и сравнивают полученные результаты по формуле (5). Вычисления заканчивают, когда неравенство (5) выполняется при всех k.