14.Регулизация зад числ. Дифференцирования

Пусть функциональная зависимость задана таблицей y_{0 =} f(x₀);…, y₁= f(x₁);…,y_{n =} f(x_n). Обычно задача интерполирования формулируется так: найти многочлен P(x) = P_n(x) степени не выше n, значения которого в точках x_i (i = 0, 1 2,…, n) совпадают со значениями данной функции, то есть P(x_i) = y_i. Геометрически это означает, что нужно найти алгебраическую кривую вида

Для любой непрерывной функции f(x) сформулированная задача имеет единственное решение. Действительно, для отыскания коэффициентов а₀, а₁, а₂ ,…, а_n получаем с-му лин ур-ний (1)

определитель которой отличен от нуля, если среди точек x_i (i = 0, 1, 2,…, n) нет совпадающих.

Решение системы (1) можно записать различным образом. Однако наиболее употребительна запись интерполяционного многочлена в форме Лагранжа и в форме Ньютона. интерполяционный многочлен Лагранжа:

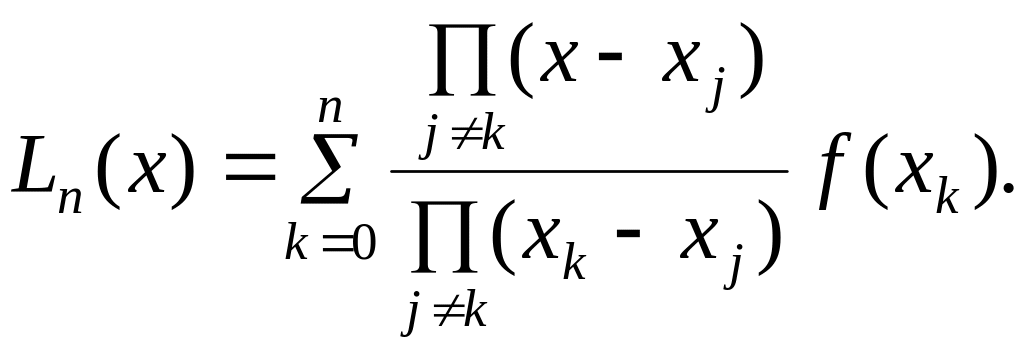(3)

Нетрудно заметить, что старшая степень аргумента х в многочлене Лагранжа равна n. Кроме этого, несложно показать, что в узловых точках значение интерполяционного многочлена Лагранжа соответствует заданным значениям f(x_i).

15,Численное дифференцирование

М етоды числ дифференцирования применяются, если исходную ф-цию f(x) трудно или невозможно продифф аналитически. Зад числ диф-ния–выбрать вычисляемую ф-цию (обычно полином) , для которой приближенно полагают y’(x)= Числ дифф-ние – некорректная зад, так как отсутствует устойч р-ния. При числ дифф-нии приходится вычитать друг из друга близкие знач ф-ции. Это приводит к уничтожению первых значащих цифр, т.е. к потере части достоверных знаков числа. А так как знач ф-ции обычно известны с определенной погрешностью, то все значащие цифры могут быть потеряны. На графике кривая (1) соотв-т уменьшению погрешности дифференцирования при уменьшении шага; кривая (2) представляет собой неограниченно возрастающий вклад неустранимой погрешности исходных данных – знач ф-ции y(x). Критерий выхода за оптимал шаг при его уменьшении – «разболтка» решения: зависимость рез-тов вычислений становится нерегулярно зависящей от величины шага. Пусть введена как интерп-нный мн-н Ньютона. В этом случае для произвольной неравномерной сетки: 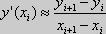, для i = 0, 1…n-1, интерполяция полиномом первой степени. 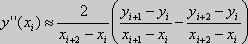, интерполяция полиномом второй степени.В общем случае 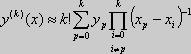. Миним число узлов, необх для вычисления k-й производной, равно k+1.Оценка погрешности при числ дифф-нии может быть осуществлена по формуле, 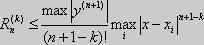,n–числоузловф-ции,k–порядок производной.Часто используются следующие формулы для трех узлов:

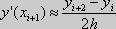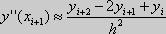, где h = x1 – x0 = const. Из общего вида интерп-ного пол-ма можно вывести ф-лы для более высокого порядка точности или для более высоких производных.

16. Регуляризация задачи численного дифференцирования

Пусть имеется двухточечн апрокс произв-й n=1, f’(x0)~(f(x0+h)-f(x0))/h, что соотв-ет замене ф-ции f линейной ф-цией, ε-погрешность вычислениязнач-й ф-ции. При выч-ии f”(x0) образ-ся предельная абсол. погр-ть 2ε/h-погр-ть прибл. Выч-ния произв по знач-м ф-ции. С другой стороны в рез-те замены произв-й её разностным аналогом мы имеем погрешность R₁^'=M₂h'/2; g(h)=2E/h+h M₂/2->min, g’(h)=-2E/h²+ M₂/2=0, h=√4E/ M₂=O(√E).Чистое диффер-ние-не корректная зад и требует построения регуляризующего алг.-ма. Простейший регуляризатор для числ-го алг-ма – регуляризация по шагу. Для для двухточ-ой аппроксимации шаг д.б. порядка О(√ε),ε-погрешность вычислениязнач-й ф-ции.