10,Метод секущих

В отличие от метода Ньютона, можно заменить производную первой разделенной разностью, найденной по двум последним итерациям, т.е. заменить касательную секущей. При этом первый шаг итерационного процесса запишется так:

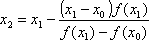
Для начала итерационного процесса необходимо задать x0 и x1, которые не обязательно ограничивают интервал, на котором функция должна менять знак; это могут быть любые две точки на кривой. Выход из итерационного процесса по условию|x_k-x_k-1|<ξ.

С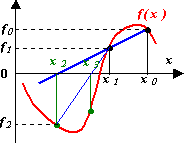 ходимость может быть немонотонной даже вблизи корня. При этом вблизи корня может происходить потеря точности, т.н. «разболтка решения», особенно значительная в случае кратных корней. От разболтки страхуются приемом Гарвика: выбирают некоторое ξx и ведут итерации до выполнения условия |x_k-x_k-1|<ξ. Затем продолжают расчет, пока |x_k-x_k-1| убывает. Первое же возрастание может свидетельствовать о начале разболтки, а значит, расчет следует прекратить, а последнюю итерацию не использовать.

11. Методы решения систем нелинейных уравнений. Квазиньютоновские методы.

Нелокальный метод Ньютона.Будем полагать ,что а) , б) , c)

(2) , ;(3)

(4) if GoTo на конец просчета else

и GoTo (2)

Справедливо(5) ,где -верхняя граница ; (6)

(2) в (6): (7) +

.Пусть , ,

, .В силу (4) означает => . < = .Итак { } { } ,(8) lim = lim = lim .Из (7)=>(9) .Из (9)=> { } , (10) lim => =1.Т-ма: Пусть оператор f, -начальная шаговая длина и -нач. приближение удовлетв. Услов.(а, б, с), тогда итерац. Пр.(2),(3).(4) со сверхлин. С лок. Квадратич. Скор. Сходится к решению уравнения (1).

(11)

12. Интер-ние. Конечные разн-ти, разн-ные отн-ния и их св-ва.

Интерполирование-поцесс построения приближающей ф-ия,сравнительно приближаемая и приближенная функции вместе с рядом своих производных совпадали с выбранной системой узлов.

Пусть f(x) задана в системе узлов , Простейшая задача интерполирования матем. выглядит так: i=0,1,..n

разностным отношением 1-го порядка назовем ф-ию

Разность 1-го порядка в числ анализе играет роль производной.

Разность отнош. 2-го порядка определяется по разности отнош. 1-го пор. .

Разнострое отношение 1-го пор обладает теми же свойствами, что и призв 1-го пор. - Разность производ ;константу можно вынести за знак;разностные отношения n-го пор от полинома n степени есть константа и , + ; = = = .Возмем , = – степень ( .

Если узлы равностоящие, то разностное отношение носит специфич. назв. Конечной разности ,

= = = ; = = = ; = = = = =

=

13. Интерполяционный полином Ньютона и его остаточный член.Интерполяционная ф-ла Ньютона позволяет выразить интерполяц мн-лен P_n(x) через знач f(x) в одном из узлов и через разделенные разности ф-ции f(x), построенные по узлам x₀, x₁,…, x_n. Эта формула явл разностным аналогом формулы Тейлора: f(x)=f(x₀)+(x-x₀)*

*f’(x₀)+(x-x₀)²f”(x₀)/2!+…(1)Прежде чем приводить ф-лу Ньютона, рассм-м сведения о разделенных разностях. Пусть в узлах x_k известны значения ф-ции f(x). Предполагаем, что среди точек x_k, k = 0,.., n нет совпадающих. Тогда разделенными разностями первого порядка называются отношения

(2)Будем рассматривать разделенные разности, составленные по соседним узлам, то есть выражения f(x₀,x₁),…,f(x_n-1,x_n) По этим разделенным разностям первого порядка можно построить разделенные разности второго порядка: (3) Аналогично определяются разности более высокого порядка. То есть пусть известны разделенные разности k-го порядка тогда разделенная разность k+1-го порядка определяется как (4)Интерполяционным многочленом Ньютона наз мн-лен (5) Показано, что интерполяционный многочлен Лагранжа совпадает с интерполяционным многочленом Ньютона.