5.Регуляризация плохо обусловленных слау.

Рассмотрим задачу Ax=y (1)

df. Говорят, что задача (1) корректна по Адамару, если

1) y Y реш. x^* X

2) x^*-единственное в X

3) x^*-устойчиво, т.е. мал изменению y соотв. малые измен. x. ,  уст-ть, есть непр-ть обрат оператора. При нарушении хотя бы одного из этих усл. задача .наз. некорректной по Адамару.

Тихонов нашел способ решать некоррек.зад.Он взял подмн-во D из X, взял образ D, AD=N.Рассм. зад Ax=y(1)A(DизX N из F)

df. Задача будет считаться корректной по Тихонову если

1) реш. x^*

2) x^*-единственное в D

3) x^*-устойчиво, т.е. мал изм-нию y соотв. малые измен. x .

Если задача корректна по Адамару, то она корректна и по Тихонову, т.е. задачи станов. корректной за счёт сужения класса корректности.

Сп-б Тих-ова:J 0< , [10^-1,10^-3]- параметр регуляризации.

Относительно понимается:

1)точное реш. x^* ;2) 0, - неотрицательный функционал.

3)мно-во образует компакты

,x=(ξ₁,…,ξ_n)удовлетв. 2) и 3) св-ву.Пусть x=(ξ₁,…,ξ_n) <r. Пусть ξ₁ –произв.знач.,а ξ₂,…,ξ_n –фиксир. → -бесконеч.посл-ть→ → ^* следовательно x=(ξ₁^*,…,ξ_n^*)

6.Обзор зад лин алгебры. Уточнение эл-ов приближ. обр ма-цы .Осн зад лин. алгебры:реш-е лин.ур-ий Ах=b, выч-ние опред-ля; нах-ние обрат. м-цы; опред-е собств знач-й и собств. векторов м-цы. Если detA=0,то СЛУ или не имеет реш-я, или имеет бесчисл-е мн-во ре-ий. Если же detA≠0, то с-ма им. ед.реш-е. Для реш-я СЛАУ используют как прямые, так и итер.методы.Определитель и обратная матрица легко вычис-ся с испол-ем м Гаусса, поскольку м-ца сводится к 3-диаг-ной, а ее опред-ль=произведению диаг-ных эл-тов: , где знак зависит от того, четн или нечетн была суммарная перестановка строк. Для выч-я обрат м-цы испол-тся .Рас-м ,где ,тогда –это n с-м с n² неизвестных,а x_ik –эл-ты обрат м-цы.Собст зн-я и в-ры. Собств вектором лин оператора A наз такой ненул вектор х, что для некот λ выпол Ax=λx. Собств знач лин оператора A наз такое число λ, для кот сущ-ет собств вектор х, т.е. ур-ние Ax = λx имеет ненулевое решение. Преобразуем р-во: .Тогда решаем , откуда нах-м собств зн-я. Выбрав базис в n-мерном лин пр-ве, можно сопоставить лин оператору квадрат. м-цу и определить для неё характ-ский мн-н

М-во всех собств знач наз спектром. После того, как спектр будет вычислен ,мы можем найти сответ-щие им собст.в-ры.Уточнение прибл.обр.м-ц. Пусть обрат.м-ца найдена каким-либо прям методом. Если вел-на , то даннае обр.м-цы нас устраивает.Если нет,то уточняем др.методом: , ,где -очередное n-ое приближение . . 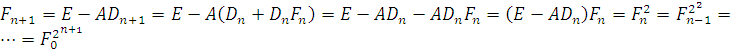Тогда .

7. Принцип сжатых отображений в огр.Обл. Банахова пр-ва.

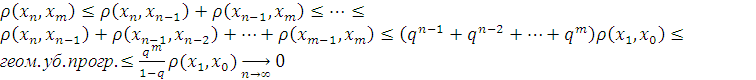Рас-м ур-ние .Пусть Ф-оператор строгого сжатия, т.е. , , . Тогда итер.процесс: , Тогда . Фундаментальность: ,то , где -реш-е ур-ния.Д-ем, что оно является реш-ем,т.е. 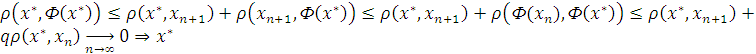-реш-е. И это реш-е единственно: пусть , -реш-я, тогда . Это значит, что в обл.D есть оператор строгого сжатия, то реш-е в D и может быть найден мет.прост.итераций. Рас-м ; ;… -сфера, за пределы кот. мы не можем выйти.

8.Методы решения нелинейных одномерных у-ий.

Рас-м ур-е f(x)=0, f( ). Пусть ф-я f(x) определена и непрерывна при всех и на [a,b] меняет знак, т.е. и ур-е имеет на (a,b) хотя бы один корень t.

Метод дихотомии. Поделим [a,b] пополам.Получаем точку , и два отрезка[a,c] и [c,b]. Если ,то корень t найден. Если нет, то из двух полученных отрезков выбираем один [ , b₁ ] такой, что , т.е. [ , b₁ ] =[a,c], если , или , b₁ ] =[c,b], если . Далее новый , b₁ ] делим пополам, получаем середину и т.д. Поэтому, если за к-е приближение этим методом к корню t ур-ния при­мем точку х_к, явл серединой полученного на к-м шаге отрезка [ , b_к ]в результате последовательного сужения данного отрезка [а, b], полагая а₁ := a, b₁ := b, то придем к неравенству . Данное нер-во, с одной стороны, позволяет утверждать, что последовательность (х_к) имеет предел — искомый корень t ур-ия; с другой стороны, явл априорной оценкой абсолютной погрешности приближенного равенства х_к , дает возможность подсчитать число шагов (итераций) метода поло­винного деления, достаточное для получения корня t с заданной точностью ε, для чего нужно лишь найти наименьшее натуральное k, удовлетворяющее нер-ву: .

Метод хорд. Пусть . Сущность метода состоит в замене кривой y=f(x) хордами, проходящими через концы отрезков, в которых f(x) имеет противоположные знаки. Метод хорд требует, чтобы один конец отрезка, для которого знак f(x)совпадает со знаком второй производной . Расчетная формула имеет вид .