8.Методы решения нелинейных одномерных у-ий.
Рас-м
ур-е f(x)=0,
f(
).
Пусть ф-я f(x)
определена и непрерывна при всех
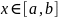и на [a,b]
меняет знак, т.е.
и ур-е имеет на (a,b)
хотя бы один корень t.
Метод
дихотомии.
Поделим [a,b]
пополам.Получаем точку
,
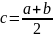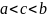и два отрезка[a,c]
и [c,b].
Если
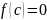,то корень t
найден. Если нет, то из двух полученных
отрезков выбираем один [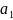
,
b1
]
такой, что
,
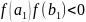т.е.
[
,
b1
]
=[a,c],
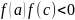если
,
или
,
b1
]
=[c,b],
если
.
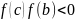Далее новый
,
b1
]
делим пополам, получаем середину и т.д.
Поэтому,
если за к-е
приближение
этим методом к корню t
уравнения примем точку хк,
являющуюся серединой полученного на
к-м
шаге
отрезка [
,
bк
]в
результате последовательного сужения
данного отрезка [а, b],
полагая
а1
:= a,
b1
:= b,
то
придем к неравенству
.
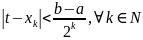Данное неравенство, с одной стороны,
позволяет утверждать, что последовательность
(хк)
имеет предел — искомый корень t
уравнения; с другой стороны, являясь
априорной оценкой абсолютной погрешности
приближенного равенства хк
,
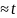дает возможность подсчитать число
шагов (итераций) метода половинного
деления, достаточное для получения
корня t
с заданной точностью ε, для чего нужно
лишь найти наименьшее натуральное k,
удовлетворяющее нер-ву: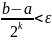
.
Метод
хорд.
Пусть
.
Сущность метода состоит в замене кривой
y=f(x)
хордами, проходящими через концы
отрезков, в которых f(x)
имеет противоположные знаки. Метод
хорд требует, чтобы один конец отрезка,
для которого знак f(x)совпадает
со знаком второй производной
.
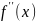Расчетная формула имеет вид
.
9 Не лок метод Ньют (квазиньют процесс)
а) f принадл C2D ||f ‘’(x)||<=k
б)||[f’(xn)]-1||<=B xn принад D
в) ε0<1
9) xn ; f(xn) 11) xn – (xn1xn2…xnn) f(xn) –f(x1)…f(xn)
f’(xn)∆xn=βnf(xn) (2) β0€[10-310-1]
xn+1= xn+∆xn (3) if ||f(xn+1)||<=ε (4) goto не конец просч else βn+1=min(1,βn||f(xn)||/||f(xn+1)||)
||f(xn+1)-f(xn)-f’(xn)( xn+1- xn)||<=k/2|| xn+1- xn||2 (5)
|| f(xn+1)||<=|| f(xn)+f’(xn)( xn+1- xn)||+k/2||xn+1 - xn||2 (6) (2) подств в (6)
|| f(xn+1)||<=||f(xn)+βn(f’(xn)||+k/2||xn+1 - xn||2<=
(1-βn)|| f(xn)||+k/2||-βn[f’(xn)]-1f(xn)||2<=
(1-βn)|| f(xn)||+k/2βn2B2||f(xn)||2=
(1-βn(1-k/2B2βn|| f(xn)||))||f(xn)||=
(1-βn(1- εn))||f(xn)||=qn||f(xn)|| (7) εn=0.5kB2βn||f(xn)|| пусть ε0=0.5kB2βn||f(xn)||<1 ||f(x1)||<=q0||f(x0)||, q0<1 ||f(x1)||<||f(x0)|| в силу (4) βn+1||f(xn+1)||= βn||f(xn)|| означает β1||f(x1)||= β0||f(x0)|| следует β1> β0
q1=1-β1(1-ε1)=1-β1(1-ε0)<1-β0(1-ε0)=q0
{ qi}↓0мон убыв { βi}↑1 мон возр
limβn+1=limβn||f(xn)||/ ||f(xn+1)||=limβ0||f(x0)||/ ||f(xn+1)||(8)
(7) след (9)
||f(xn)||<=Пqi||f(x0)||<=q0n+1||f(x0)||→0 при n→∞ из (9)след {xn}→x* (9) в (8)
limβn+1=∞ след сущ n0 и βn+1=1
Теор Пусть оператор f, β0 – начальная шагов длина и x0 начальн прибл удв усл а)б)с) тогда итерац процесс (2)-(4) со сверх лин лок квадр скоростью сходится у решению ур (1) ||f(xn+1)||<=εn||f(xn)||=0.5KB2||f(xn)||2=q||f(xn)||2
||f(xn+1)||<=q||f(xn)||2