
- •1.Прямые методы решения слау.
- •2)Lu-разложение.
- •2.Метод трехдиагональной матричной прогонки.
- •4. Задачи линейного программирования(лп). Регуляризация задач лп.
- •5.Регуляризация плохо обусловленных слау.
- •7. Принцип сжатых отображений в огр.Обл. Банахова пр-ва.
- •6.Обзор задач линейной алгебры. Уточнение эл-ов приближ. Обратной ма-цы .
- •8.Методы решения нелинейных одномерных у-ий.
- •9 Не лок метод Ньют (квазиньют процесс)
- •26 Полиномы Чебышева(пч)
- •33.Жёсткие начальные задачи. Неявный метод Эйлера и его устойчивость.
- •34.Жёские начальные задачи. Неявный метод средней точки и его устойчивость.
- •35.Жёсткие задачи. Неявный метод трапеций и его устойчивость.
- •25.Аппроксимация функции с помощью кубического сплайна
- •15,Численное дифференцирование
- •10,Метод секущих
- •38. Нахождение наибольшего по модулю собственного значения матрицы.
- •11. Методы решения систем нелинейных уравнений. Квазиньютоновские методы.
- •12. Интерполирование. Конечные разности, разностные отношения и их свойства.
1.Прямые методы решения слау.
Все методы решения СЛАУ можно разбить на два класса: прямые и итерационные. Прямые методы - методы, которые приводят к решению за конечное число арифметических операций. Если операции реализуются точно, то и решение также будет точным (поэтому прямые методы наз. ещё точными методами)
Мы рассматриваем численное решение таких СЛАУ, у которых число уравнений совпадает с числом вещественных неизвестных, причем предполагается наличие единственного решения, если существование и единственность не следует из каких-либо условий.
Итак, изучается вопрос о численном решении системы …(1) или иначе, векторно-матричных уравнений Ах=b. (1a) где b – вектор свободных членов x - вектор неизвестных (он же в другой интерпретации может означать и вектор-решение) с вещественными координатами, а А - вещественная n*n-матрица коэффициентов данной системы. Эффективность способов решения системы (1) во многом зависит oт структуры и свойств матрицы А: размера, обусловленности, симметричности, заполненности (т.e. соотношения между числом ненулевых и нулевых элементов), специфики расположения ненулевых элементов в матрице и др.
Прямые методы решения СЛАУ:
1.Метод Гаусса(с выбором главного элемента по столбцам).
2.LU-разложение.
3.Метод квадратного корня.
1) Метод Гаусса. Суть: последовательное исключение неизвестных. Поэтапно приводим систему к треугольному виду, исключая последовательно сначала x1 из второго, третьего, …, n-го у-ний, затем x2 из 3-го, 4-го,..,n-го у-ий преобразованной системы, и т.д. Для 1-го преобраз. коэф. ищем по ф-ле:
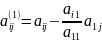 .
.
 .
где i,j=2,3…
.
где i,j=2,3…
Продолжая этот процесс на (n-1)-ом этапе прямого хода МГ приведём с-му к треугольному виду. Треугольная структура с-мы позволяет последовательно вычислять знач. неизвестных , начиная с последнего. Этот процесс наз. обратным ходом МГ.
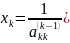 )
)
Числа, на которые проводится деление в МГ, наз. ведущими или главными элементами. Главный элемент - наибольший
эл-т в столбце (для исключения деления на нуль и уменьшая погрешность вычислений)
2)Lu-разложение.
Если все главные
миноры квадратной м-цы А отличны от
нуля =>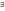 нижняя L
и верхняя U
треугольная м-цы, что A=LU.
Если э-ты диагонали одной из м-ц L
или U
–фиксир.(ненулевые), то такое разложение
единственно. u11=a11,…,u1n=a1n;
ln1u11=an1,
ln1u1n+
…+unn=ann.
нижняя L
и верхняя U
треугольная м-цы, что A=LU.
Если э-ты диагонали одной из м-ц L
или U
–фиксир.(ненулевые), то такое разложение
единственно. u11=a11,…,u1n=a1n;
ln1u11=an1,
ln1u1n+
…+unn=ann.
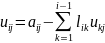 . (где
i
. (где
i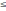 j)
j)
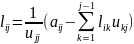 .
(где i>j)
.
(где i>j)
Заменяем A
в Ax=b
=>LUx=b
решаем с-му
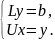 => сначала вычисляем y
из Ly=b
затем полученный результат подставляем
в Ux=y
и находим x.
=> сначала вычисляем y
из Ly=b
затем полученный результат подставляем
в Ux=y
и находим x.
3)Метод квадратного корня(М. Холецкого).
Пусть A-симметричная
м-ца (aij=aji).
Представляем её в виде A=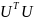 ,
где U=
,
где U=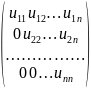 реш. с-мы сводится к реш. 2-ух треугольных
с-м :
реш. с-мы сводится к реш. 2-ух треугольных
с-м :
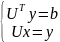 и нах. По ф-лам:
и нах. По ф-лам:
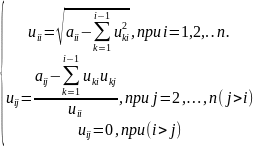
Замечание:
Вычислительные затраты на операции
умножения и деления в МГ- О(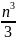 )
, в МКК- О(
)
, в МКК- О(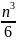 )
)
