24. Релятивистский закон сложения скоростей

Пусть в системе отсчета K’ материальная точка движется вдоль оси х’ спостоянной скоростью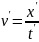 Система K’ движется относительно системы K в том же направлении со скоростью v , Определим, чему равна скорость материальной точки vo, относительно системы K, т.е. чему равно 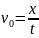: Пусть при 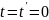м.т. находится в начале координат, причем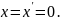 Для системы K: 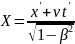; 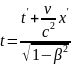Подставляя и t в формулу для vo 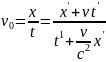Делим числитель и знаменатель на t 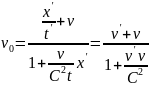. Это равенство выражает собой релятивистский закон сложения скоростей. При малых значениях скоростей v’ во много раз меньше с и v во.м.р.м с имеем во.м.р.м. 1 и v0=v’+v т.е. релятивистский закон сложения скоростей переходит в классический

25.инвариантные величины.

Инвариантные величины - величины не зависящие от выбора системы отсчёта ( неизменные, постоянные, одинаковые ), например, масса (m) Напр., если рассматривать движение матер. точки в двух системах координат, повёрнутых одна относительно другой на нек-рый угол, то проекции скорости движения в них будут разными, но квадрат скорости, а следовательно, и кинетич. энергия будут одинаковыми, т. е. кинетич. энергия инвариантна относительно поворота в пр-ве системы отсчёта.