16.Кинетическая энергия вращения.

Рассмотрим абсолютно твердое тело, вращающееся около неподвижной оси z, проходящей через него (рис. 24). Мысленно разобьем это тело на маленькие объемы с элементарными массами т1, т2 ,..., тn , находящиеся на расстоянии r1, r2,..., rn от оси. При вращении твердого тела относительно неподвижной оси отдельные его элементарные объемы массами mi опишут окружности различных радиусов ri, и имеют различные линейные скорости vi. Но так как мы рассматриваем абсолютно твердое тело, то угловая скорость вращения этих объемов одинакова: (1) Кинетическую энергию вращающегося тела найдем как сумму кинетических энергий его элементарных объемов: или используя выражение (1) получаем: где Jz — момент инерции тела относительно оси z. Таким образом, кинетическая энергия вращающегося тела

17.Момент силы. Плечо силы. Линия действия силы.

Моментом силы относительно неподвижной точки О называют векторное произведение радиус вектора проведенного из точки О в точку приложения силы на саму эту силу. ; Плечо силы относительно точки, кратчайшее расстояние от данной точки (центра) до линии действия силы, т. е. длина перпендикуляра, опущенного из этой точки на линию действия силы ( - плечо силы).Момент силы относительно точки О есть векторная величина, а момент силы относительно оси проходящий через эту точку есть скалярная величина. Моментом силы относительно неподвижной оси z называется скалярная величина равная проекции на эту ось вектора М момента силы, определенного относительно произвольной точки О данной оси z. Значение момента не зависит от выбора положения точки О на оси z Линия действия силы - прямая, по которой направлена сила.

18.Уравнение динамики вращательного движения.

Согласно уравнению второй закон Ньютона для вращательного движения По определению угловое ускорение 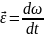и тогда это уравнение можно переписать следующим образом c учетом предыдущего: Это выражение носит название основного уравнения динамики вращательного движения и формулируется следующим образом: изменение момента количества движения твердого тела dL, равно импульсу момента Mdt всех внешних сил, действующих на это тело.

19.Понятие момента импульса.

Моментом импульса материальной точки А относительно неподвижной точки О называется физическая величина, определяем векторным произведением: , где r – радиус вектор из точки О в точку А; p=mv импульс материальной точки. Модуль вектора момента импульса ; - угол между векторами r и p.

20.Закон сохранения момента импульса

Пусть дана система частиц, положение которой относительно т. О определяется соответственно радиус векторами. Запишем для каждой материальной точки второй закон ньютона (-/8/-). По третьему закону Ньютона тела взаимодействуют с одинаковыми по модулю силами, поэтому плечо силы одинаковое и F_внутр = 0 => - закон изменения момента импульса, производная от момента импульса системы по времени равна суммарному моменту внешних сил, т.е. изменить момент импульса могут только внешние силы, а внешние силы не действуют или их результирующий момент равен нулю, получим => L=const.