32. Спектральный анализ сигналов в случае прямой модуляции.

Функция постоянного сигнала – это несущий сигнал. Пусть поcтоянный сигнал с амплитудой А , используется в качестве несущего сигнала. Закон изменения которого записывают следующим оброзом: х(t)=A + U cosΩt

Где: Ω-частота полезного сигнала;

ω - частота несущего сигнала(сигнал изменяется по закону косинусов).

-Несущий сигнал

х(t)=A + U cosΩt

А

A

0

мплитуда полезного сигнала меняется по закону косинуса. Разложение этой функции х(t)…… в ряд Фурье даёт спектр гармоник (это составные ряда в котором имеются следующие не соответствия). Графическое отображение спектральной плотности (математической функции) представлена на рисунке в конце билета.

Здесь анализируются 2-е составляющие – постоянная с частотой 0, и 2-ая (гармоника) с частотой ω низкочастотная.Рост на оси частот, т.е. рост от 0 до ω-частот, называется полосой пропускания (ширина спектра (П)) П = Ω.Это связано с тем что: С.И. использующее такой вид управления (прямая модуляция) должно иметь ширину амплитудно – частотной характеристики (полосу пропускания частоты) не меньше чем П, иначе форма сигнала воспроизводимая средством измерения будет искажена.

33. Спектральный анализ сигналов в случае амплитудной модуляции

Полезный сигнал у нас будет косинусоидальный: х(t)=A + U cosΩt

В измерительной технике частоту ω выбирают много больше частоты полезного сигнала ω>>Ω. Вид такого полезного сигнала будет такой(смотри рисунки в конце билета).Пусть функция несущего сигнала х(t)=А cos ωt.

Р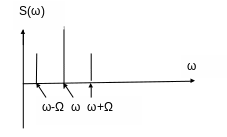 азложение этой функции в ряд Фурье даёт спектр с частотой ω (или частота несущего колебания), гармонику с частотой ω+Ω и ω-Ω. Таким образом ширина спектра составляет 2Ω-низкочастотная. Это значит, что С.И. предназначенное для усиления или преобразования должно иметь А и Х шириной не менее 2ω.На рисунке 1-я линия это ω-Ω, 2-я линия это ω, а 3-я линия это ω+Ω.

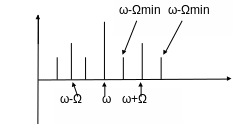
В случае если полезный сигнал (модулированное колебание будет иметь более сложную форму чем cos ωt, в спектре появятся дополнительные низко частотные гармоники. В спектре появится составляющая c min и max значением Ω,а на графиках спектральной плотности это ω показывает как появляются гармонтки с частотами, т.е. спектр расширился и δ=2Ωmax. Где 1-я линия это ω-Ωmin;

2-я линия это ω-Ω; 3-я - ω-Ωmax

4-я-ω; 5-я – это ω+Ωmin;

6 – я –это ω+Ω; 7-я – это ω+Ωmax

Первый рисунке который представлен ниже, это несущий сигнал (х(t)=А cos ωt), второй рисунок это полезный сигнал(х(t)=А cos Ωt). Ну а третий это амплитудно - модулированный сигнал, по закону несущего сигнала. А – это амплитуда несущего сигнала, она будет равна: х(t)=(А +А cosΩt) cosωt

С

0

пектральный анализ сигналов в случае частотной модуляции.

х(t)= Acosωt

x(t)=AcosΩt

Где: Ω – низкочастотный сигнал;

ω – высокочастотный несущий сигнал.

Закон изменения (ω - это закон изменения по косинусоидальному закону): ω ± ωcosΩ

Модулирующая функция имеет постоянную амплитуду.

С

ω -2Ω

пектр (математический анализ разложенный в ряд Фурье) дает спектральный состав. Спектральный состав функции в случае модуляции выглядит так:

Ш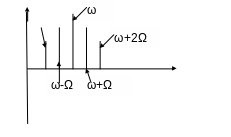 ирина этого спектра (П):

П=4Ω

В случае если модулированная функция (низкочастотный сигнал) имеет более сложный характер нежели x(t)=AcosΩt, спектральный состав изменится. Добавится еще одна третяя гармоника.

П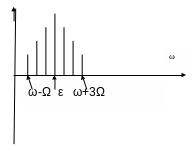 =6Ω

Это нужно для того, чтобы правильно выбрать С.И. Каждое С.И. имеет амплитудно-частотную характеристику, которая имеет завалы (спад коэффициентов усиления элементов С.И. за счет непостоянства сопротивления реактивных элементов х х ). Завалы – это спад коэффициентов усиления, элементов С.И. за счет непостоянства сопротивлений реактивных элементов:

х =

х =

В связи с этим при известном способе управления сигналом требуется выбрать такое С.И. у которого полоса (заштриховка) была равна или больше ширины спектра результирующей функции. В случае соответствия С.И. этой функции у(t) не будет соответствовать х(t), т.е. возникают искажения формул сигнала, что приводит к погрешности измерений в измеряемом параметре.