
- •1.Понятие отображения. Числовая функция одной переменной, нескольких переменных, вектор-функция скалярного аргумента.
- •4.Бесконечно малые, ограниченные, бесконечно большие, отделимые от нуля величины. Их свойства.
- •5.Простейшие свойства пределов.
- •8. Признаки существования предела.
- •34(9) Первый и второй замечательные пределы. Их следствия. Первый замечательный предел
- •11. Непрерывность отображения. Непрерывность числовой функции одной переменной, нескольких переменных.
- •37(12)Точки разрыва,классификация точек разрыва.
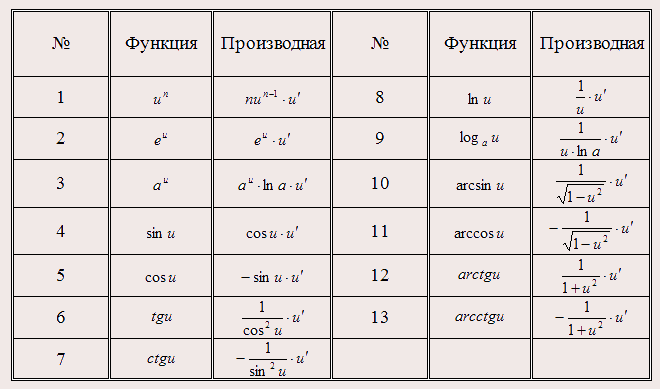
- •14. Дифференциал отображения. Дифференциал и производная числовой функции одной переменной. Таблица производных. Дифференцируемость.
- •17.Производные неявной функции одной и нескольких переменных.
- •Частные производные высших порядков
- •23. Разложение по формуле Маклорена некоторых элементарных функций.
14. Дифференциал отображения. Дифференциал и производная числовой функции одной переменной. Таблица производных. Дифференцируемость.
Пусть есть отображение, кот вычисляется так: ∆y=f(x+∆x)-f(x) (1). В общем случае ∆y зависит не только от ∆х , но и от нач.вектора х. Т.е. ∆y=∆y(x;∆x). Пусть при ∆х<ε приращение отображения (1) можно представить в виде ∆y=dy+0(|∆x|) (2) , где dy= dy(x;∆x). 0(|∆x|) – это БМ величина высшего порядка по сравнению с ∆x, т.е. при |∆x|→0 lim 0(|∆x|)/|∆x|=0. Величина dy называется дифференциалом отображения. Отображение, для кот. существует дифференциал, т.е. имеет место (2) , называется дифференцируемым. Понятие дифференцируемости можно рассм для отдельных точек Х или его подмножеств. Это общее понятие дифференциала. Его можно конкретизировать: 1) y=f(x): R→R; 2) для числ ф-ции многих переменных y=f(x1,x2…xn): Rn→R ; 3) для вектора ф-ции скалярного аргумента y=f(с палочкой)(x): R→ Rn.
Линейное отображение по ∆x будет иметь вид a*∆x, где ∆xϵR, aϵR; При этом a может зависеть от нач.вектора х. Тогда dy=a(x)∆x (5). Отсюда согласно (2) ∆y= a(x)∆x+0(∆x). Разделим на ∆x и перейдем к пределу (все пределы при ∆x→0) lim ∆y/∆x=lim a(x) + lim 0(∆x)/ ∆x; y′=a(x); Таким образом, a(x) – производная ф-ции f(x), тогда (5) принимает вид dy=f ′(x)∆x. При рассм ф-ции y=x y′=x′=1, тогда dx=∆x, => dy=f ′(x)dx – дифференциал числовой ф-ции одной переменной. Отсюда следует, что f ′(x)= dy/ dx, т.е. производная ф-ции y=f(x) равна отношению дифференциала ф-ции к дифференциалу аргумента.
41(16)
Производные Функций Нескольких Переменных.
Рассмотрим
функцию u
= F(x),
определенную в некоторой области D.
Пусть
![]() −
фиксированная точка. Дадим координате
х1
приращение
−
фиксированная точка. Дадим координате
х1
приращение
![]() .
Если существует конечный предел
.
Если существует конечный предел
![]() ,
то он называется частной
производной
функции F(x)
по переменной х1
и обозначается
,
то он называется частной
производной
функции F(x)
по переменной х1
и обозначается
![]()
Аналогично определяются частные производные по всем остальным переменным.
Замечания.
1. Частная производная по какой либо переменной есть обычная производная, при условии, что все остальные переменные – константы.
2. Последнее обозначение, в отличие от функций одной переменной, не равно частному от деления двух дифференциалов, а является неразрывным символом.
В частном случае двух переменных частная производная равна тангенсу наклона касательной к сечению поверхности плоскостью, перпендикулярной ко второй переменной.
Полный дифференциал функции нескольких переменных.
Пусть
задана функция
![]() .
Если аргументу
.
Если аргументу
![]() сообщить
приращение
сообщить
приращение
![]() ,
а аргументу
,
а аргументу
![]() –
приращение
–
приращение
![]() ,
то функция
получит
приращение
,
то функция
получит
приращение
![]() ,
которое называется полным
приращением функции
и определяется формулой:
,
которое называется полным
приращением функции
и определяется формулой:
![]() Функция
,
полное приращение
которой
в данной точке может быть представлено
в виде суммы двух слагаемых (выражения,
линейного относительно
и
,
и величины бесконечно малой высшего
порядка относительно
Функция
,
полное приращение
которой
в данной точке может быть представлено
в виде суммы двух слагаемых (выражения,
линейного относительно
и
,
и величины бесконечно малой высшего
порядка относительно
![]() ):
):
![]() ,
где
,
где
![]() и
и
![]() стремятся
к нулю, когда
и
стремятся
к нулю (т.е. когда
стремятся
к нулю, когда
и
стремятся
к нулю (т.е. когда
![]() ),
называется дифференцируемой
в данной точке.
Линейная (относительно
и
)
часть полного приращения функции
называется полным
дифференциалом
и обозначается
),
называется дифференцируемой
в данной точке.
Линейная (относительно
и
)
часть полного приращения функции
называется полным
дифференциалом
и обозначается
![]() :
:
![]() ,
где
,
где
![]() и
и
![]() –
дифференциалы независимых переменных,
которые, по определению, равны
соответствующим приращениям
и
–
дифференциалы независимых переменных,
которые, по определению, равны
соответствующим приращениям
и
