• 18.) Точечные оценки параметров нормального

РАСПРЕДЕЛЕНИЯ.

Несмещенной эффективной и состоятельной оценкой МО явл. выборочная средняя: 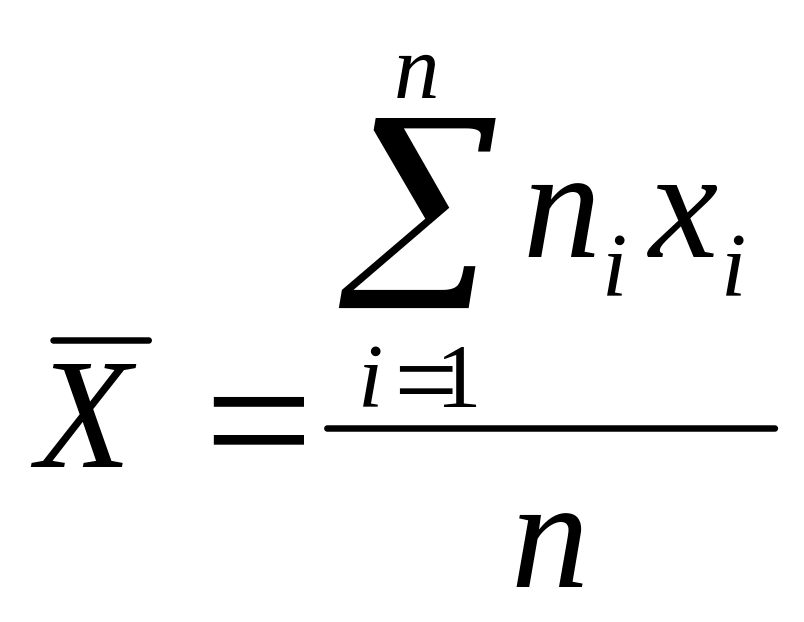. Выборочная дисперсия D_в=S² есть смещенная оценка дисперсии нормального распределения. Можно доказать, что: М(S²)=[(n-1)/n]*D(x);

M(S²)=[(n-1)/n]*². Для того, чтобы получить несмещенную оценку мы должны исправить выборочную дисперсию введя коэф. n/(n-1) – коэф. Бесселя. . Исправленная выборочная дисперсия есть несмещенная оценка дисперсии нормального распределения. Она вычисляется по формуле: . Поправка Бесселя чувствительно отличается от 1 только для малых n. С возрастанием n она все ближе к 1 и при n>30 практически не отличается от 1. Т.е. при n>30 дисперсию можно не исправлять, а брать D_в как несмещенную оценку нормального распределения.

• 19.) Доверительный интервал. Доверительная

ВЕРОЯТНОСТЬ

Пусть сделана выборка объема n. Для оценки распределения СВ Х генеральной совокупности применяются точечные оценки параметров распределения генеральной совокупности и интервальные оценки. Интервальной оценкой (доверительным интервалом) для оценки некоторого параметра  (тэта), например МО, называется угловой интервал , в котором с заранее заданной вероятностью Р=1- содержится оцениваемый параметр.

Опр.: Доверительным интервалом для оценки параметра  назыв. интервал для которого . Вероятность Р=1- - называется доверительной вероятностью.

Выбор доверительной вероятности Р=1- производится исходя из конкретных условий задачи.

• 20.) Построение доверительного интервала для мо при известных .

Пусть сделана выборка из генеральной совокупности объема n. Найдена выборочная средняя: 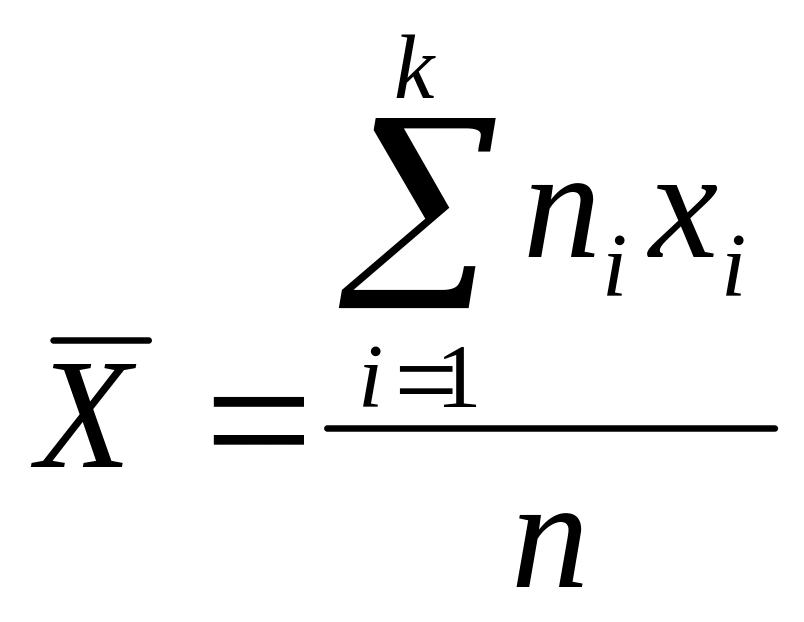. Требуется определить МО а, при условии, что среднеквадратическое отклонение  известно; предполагается, что распределение нормальное. Доверительный интервал для МО в этом случае находится по формуле:

, где t находится из условия 2Ф(t)=1-.; n – объем выборки. р=1- - доверительная вероятность заранее заданная. Ф(t)=(1-)/2 – функция Лапласа (нах. по табл.). ; - минимальный объем выборки при заданной . С возрастанием n  - уменьшается, т.е. доверительный интервал сужается, оценка становится более точной. С возрастанием доверительной вероятности р=1-, t – возрастает, доверительный интервал расширяется, оценка становится менее точной.

• 21.) Доверительный интервал для св х распределенной по нормальному закону при неизвестном .

Пусть СВ Х предположительно распределена по нормальному закону, параметры которого неизвестны. Чтобы найти интервальную оценку МО а, найдем точечные оценки а и . Для . Тогда доверительный интервал с доверительной вероятностью р=1-= будет иметь вид: , где t_,n – находится в таблице по  и n.

Замечание: такая оценка производится при малых n, n<30.

• 22.) Доверительные интервалы для оценки среднеквадратического отклонения  нормального распределения.

Пусть требуется определить среднеквадратическое отклонение  нормального распределения по известному исправленному среднеквадратическому отклонению. Пусть задана доверительная вероятность р=1-=.Пусть объем выборки =n,тогда доверительный интервал имеет вид , q – находится в табл. по известному  и n.

Замечание: Иногда в таблице сразу даны два значения q, q₁ и q₂.