• 14.) Эмпирическая функция распределения.

Опр.: Эмпирической функцией распределения СВ Х назыв. функция F^*(x) означающая относительную частоту события Х<x, т.е. F^*(x)=n_x/n, где n_x – сумма частот вариант <x.

Т.о. если дан стат. ряд

xi	x1	x2	…	xk
Wi	W1	W2	…	Wk

, то . Для интервального стат. ряда берутся суммы относительных частот вариант попавших в предыдущие интервалы.

Свойства эмпирической функции:

1. 0F^*(x)1.

2. F^*(x) – неубывающая функция.

3. Если x₁ – минимальная варианта, а х_к – максимальная, то F^*(x₁)=0, а .

4. При n эмпирическая функция распределения стремится по вероятности F(x) (функция распределения СВ) по теореме Бернулли закона больших чисел.

• 13.) Графическое изображение стат. Рядов. Полигон.

ГИСТОГРАММА.

Графическим изображением дискретного стат. ряда служит полигон. На оси ОХ откладываем варианты. В каждой из этих точек восстанавливаем перпендикуляр, длина которого пропорц. соответствующим частотам. Затем концы соседних перпендикуляров соединяем отрезками прямых, а концы крайних перпендикуляров соединяют с серединами соседних интервалов частоты которых =0. В результате получаем замкнутую фигуру (полигон).

Для графического изображения интервального стат. ряда пользуются гистограммой. На оси ОХ откладывают интервалы и на каждом из них как на основании строят прямоугольник с высотой пропорциональной частоте интервала. Чаще всего эту высоту берут равной плотности относительной частоты на данном интервале, т.е. величине m_i/(n*h), где m_i/n – относительная частота, h – длина интервала. Площадь каждого прямоугольника S=m_i/n (относительной частоте). Вся площадь занимаемая гистограммой =1.

КУММУЛЯНТА. ОГИВА.

Накопленной частотой (относительной частотой) в точке х назыв. суммарную частоту (относит. частот) членов стат. ряда со значением вариант меньше чем х. Если в стат. ряде вместо частот или относительных частот записать соответственно накопленные частоты или относительные частоты, то получится кумулятивный ряд. Для графич. изображения кумулятивных рядов служат кумулянты и огивы.

Кумулянта строится след. образом: на оси абсцисс отмечают точки соответствующие границам интервалов или значен. вариант и в каждой точке восстанавливают перпендикуляр длина которого пропорциональна накопленной относительной частоте. Концы соседних перпендикуляров соед. отрезками. Полученная ломаная линия назыв. кумулянтой.

Если на горизонтальной оси откладывать накопленные относительные частоты, а на вертикальной значения вариант, то полученная при этом кривая назыв. огива.

• 15.) Числовые характеристики статистического ряда.

I. Средние значения.

Выборочной средней (выборочная средняя арифметич.) назы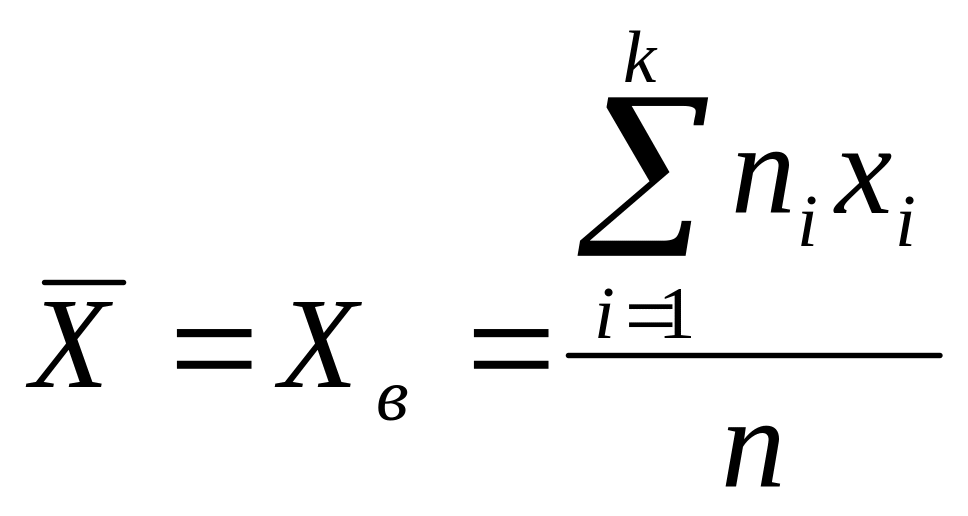в. . Если задан интервальный ряд, то представителем каждого интервала явл. его середина. и выборочная средняя х находится аналогично, где х_i – середины интервалов.

Выборочная средняя для сгруппированных данных и не сгруппированных данных отличаются между собой, но незначительно.

Медиана

Медианой [Me] - назыв. варианта стат. ряда, расположенного в порядке возрастания, занимающая серединное положение. Для нечетного n медиана занимает положение (n+1)/2, для четного n – среднее арифметическое вариант n/2 и (n/2 +1).

Для интервального ряда медиану находят с помощью линейной интерполяции.

Мода

Модой [Mo] – назыв. варианта имеющая наибольшую частоту. Для интервального ряда мода есть середина интервала имеющего наибольшую частоту. Графически мода представляет из себя значение Х, которому соответствует максимум ординаты полигона.

Картили (Квартили).

Медиана есть значение варианты занимающее срединное положение в вариационном ряду. Если найти еще раз медианы каждой половины, то получим значения вариант назыв. картилями. [Q₁ – 1-й картиль; Q₃ – 2-й картиль; Q₂ – Me].